倍数特性
整除型
(1)口诀法:(常用于3、4、5、9)3/9看各个位数字之和,5看末位,4看末两位。
3/9 -> 看各位数字之和能否被3/9整除,例:124345
2/5 ->看数字末一位能否被2/5整除,例:12125
4/25 ->看数字末两位能否被4/25整除,例:12164
(2)拆分法(没口诀、常用于7、13)
一个数=接近且明显能被整除的数+-零头,只看零头
例:623 ➗ 7 把623拆成7的倍数+-零头,只看零头能否被7整除
(3)因式分解(复杂倍数,常用于6、12、18、24等)
因式分解成两个互质(互质指两数没有公约数)的数,同时满足能被这两个数整除
例:24=3✖️8
余数型
特性:均分、多几个、少几个
若总数 = ax + b, 则(总数 - b) 能被a整除。(a,x均为整数)
比例型
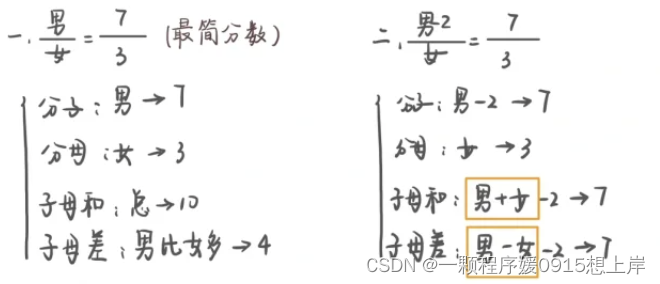
题干特征:分数、比例、百分数、倍数
对象特征:不可分割整体(人、年龄等整数)
余数问题 三则运算
口诀:余同加余,和同加和,差同减差,公倍数做周期
解释:
- 余同加余。例如“一个数除以7余1,除以6余1,除以5余1”,可见,所得余数恒为1,则取1,被除数的表达式为210n+1
- 和同加和。例如“一个数除以7余1,除以6余2,除以5余3”,可见,除数与余数的和相同,取此和8,被除数的表达式为210n+8
- 差同减差。例如“一个数除以7余3,除以6余2,除以5余1”,可见,余数与除数的差相同,取此差4,被除数的表达式为210n-4
注意:前面的210是5、6、7的最小公倍数,此即为公倍数做周期
倍数特性之增长率型
充分利用已学过的资料分析来解决数量问题
- 分析关系:基期、现期
- 结合选项,做猜结合
方程问题
普通方程:一个未知数x
设未知数技巧
- 设小不设大 (高照是你(x)的两倍)
- 出现比例设份数 (高照:上岸 = 3:2 =》3x 2x)
- 设中间量 ta ->(+10)高(-20)<-你
普通方程:多个未知数设XYZ
- 存在多个未知数,设XYZ
- 抓住问题消元求解 只用留下要的,消好消的
小技巧:
普通方程:A与非A
方法一:
- 列式
- 总 = (非A+非B+非C)/2
- A = 总 - 非A
非A = 总 - 非B - 非C
方法二:问谁非谁
A = ( 非B + 非C - 非A)/ 2
不定式方式
- 奇偶 3x(奇)+4y (偶)= 25
- 倍数(公因子) 7x + 3y = 60 (60、3y都是3的倍数,x是3n)
- 尾数
- 代入

等差数列

周期问题
周期余数

周期相遇

星期日期问题









 本文介绍了数学中关于倍数特性的各种解题方法,包括整除型口诀、拆分法、因式分解以及处理余数、比例、增长率型问题的策略,还涵盖了方程设置技巧和特殊数列如等差数列与周期问题的解决方案。
本文介绍了数学中关于倍数特性的各种解题方法,包括整除型口诀、拆分法、因式分解以及处理余数、比例、增长率型问题的策略,还涵盖了方程设置技巧和特殊数列如等差数列与周期问题的解决方案。
















 6834
6834

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








