论文笔记------------SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

---

前言

本博客介绍了卷积、谱图、傅里叶变换、拉普拉斯矩阵等知识，接着对于该论文进行了自己的理解与解读，同为研究生的xdm一起加油！

---

一、卷积

1.定义

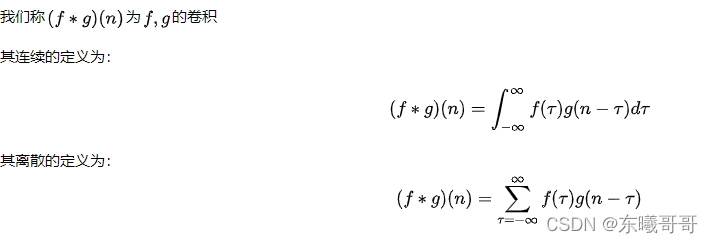
连续的定义很好理解，就是在定义域上求积分。
离散的定义也很好理解（手动狗头），就是积分的微观表达，累加求和。

我们发现这两个式子有着共同特征：

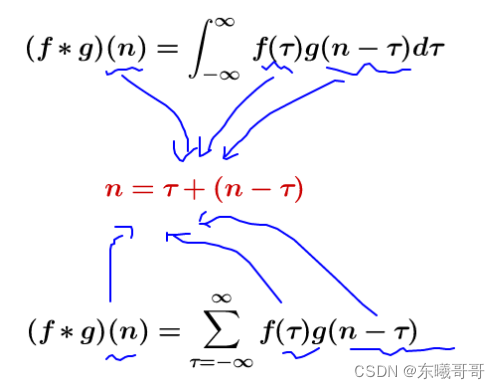
这个特征转换成更好理解的概念就是：

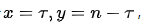
那么指的就是x+y=n的这些曲线：

我们可以看到，随着n的不断变化，这些不同的曲线就形成了一个函数簇。

2.举个栗子

（1）掷骰子

	假设有两个骰子，我们把它们掷出去，希望知道：两个骰子点数加起来等于4的概率是多大？

这个问题的核心是，两个骰子加起来要等于4，和我们对于卷积的定义相契合。
那我们就把问题转换为：

那么符合条件的情况有如下三种：

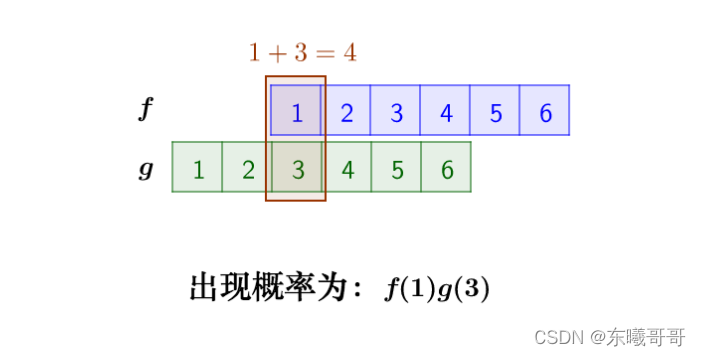
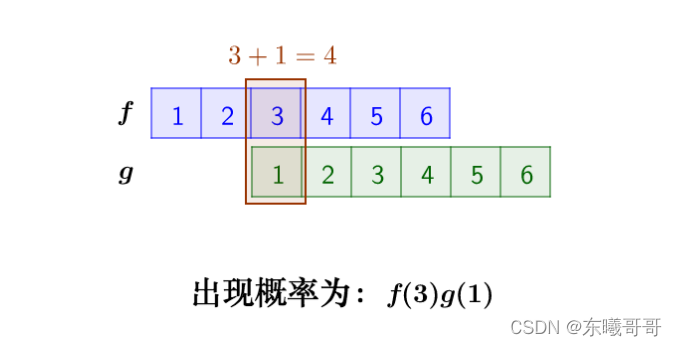
综上，概率为：

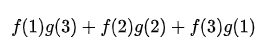
在这里应该用离散的定义表示：

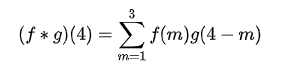
3.二维离散卷积

之前我们讨论的都是一维的卷积公式，那么从一维推广到二维，我们可以类推得到：



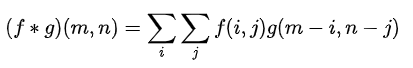
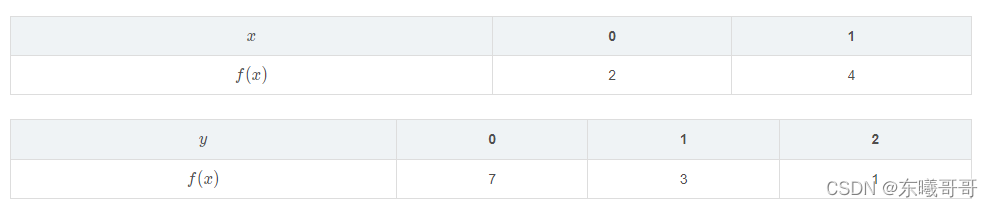
以下是所有x，y的组合情况，并分别对于每种情况进行计算：

二维时，就变成了两个矩阵进行卷积：

4.数学中的卷积与CNN中的卷积区别

事实上，数学中的卷积和卷积神经网络中的卷积严格意义上是两种不同的运算

数学中，”卷积核“矩阵需要进行如下翻转后，再与f(x)进行内积：

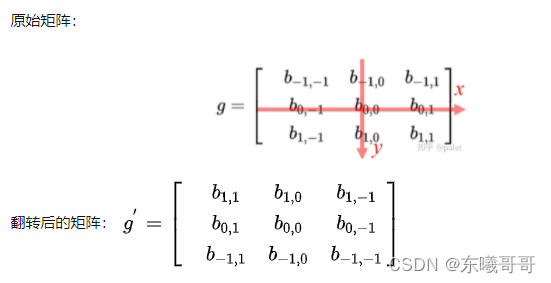
CNN中：
卷积核是这么计算的：

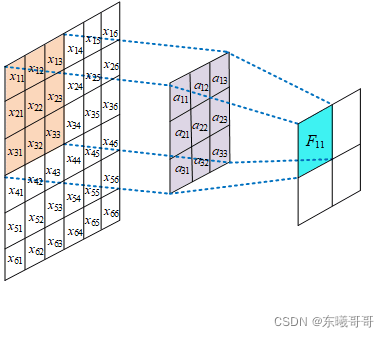
综上，我们可以知道以下几点：
（1）数学中卷积，主要是为了诸如信号处理、求两个随机变量和的分布等而定义的运算，所以需要“翻转”是根据问题的需要而确定的。
（2）卷积神经网络中“卷积”，是为了提取图像的特征，其实只借鉴了“加权求和”的特点。
（3）还有一点一定要说的是：数学中的“卷积核”都是已知的或者给定的，卷积神经网络中“卷积核”本来就是trainable（需要训练）的参数，不是给定的，根据数据训练学习的，那么翻不翻转还有什么关系呢？因为无论翻转与否对应的都是未知参数！

这里有几篇文章写的不错，我也是从这里参考理解的：
如何通俗易懂地解释卷积
数学中的卷积与卷积神经网络中的卷积，二者是不同的

---

二、spectral domain（频谱域）

1.Spatial domain

翻译过来就是空间域，是最直观感受GCN逐层传播算法的域，即：节点 的Embedding是其所有邻居节点Embedding(包括自己的Embedding)的聚合结果。因此在一些文献上spatial domain又被称做"vertex domain"。

2.spectral domain

但是与CNN所应用的图像不同，空间域中图节点邻居的数目不是一定的，而且节点之间没有相对的次序性。这就产生了一个问题，对于不同邻居个数的节点，卷积怎么定义呢？这就引出了spectral domain的概念。spectral domain，即频谱域，借助卷积定理，我们可以通过定义频谱域上的卷积操作来得到空间域图上的卷积操作。

---

三、谱图理论

那么图在频谱域上是如何表示的呢，这就引出了我们第二个概念：谱图理论，谱图理论主要研究的是图的拉普拉斯(Lapalacian)矩阵的特征值和所对应的特征向量对于图拓扑性质的影响，是对图空间拓扑的数学描述。

1. 拉普拉斯矩阵

（以下图均视为无向图）

1.1 定义

Labeled graph：原始图G。
Degree matrix：图G的度矩阵D（每个值表示每个节点的度数，所以只在主对角线上有值，其余值都为0）。
Adjacency matrix：图G的邻接矩阵A。（节点i与节点j有边，值为1,；没有边，则为0）
Laplacian maxtrix：图G的拉普拉斯矩阵L，通过D-A得到。

此外，拉普拉斯矩阵还有以下变种：

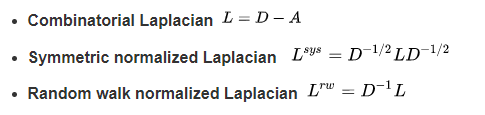
论文中一般用的是第二种定义，正规拉普拉斯矩阵。

1.2 性质

（1）拉普拉斯矩阵是半正定矩阵。
（2）特征值中0出现的次数就是图连通区域的个数。
（3）最小特征值是0（特征值非负），因为拉普拉斯矩阵每一行的和均为0。
（4）最小非零特征值是图的代数连通度。
（5）是实对称矩阵，有n个线性无关的特征向量。
（6）这些特征向量都可以正交单位化而得到一组正交且模为 1 的向量。

从（5）可得，拉普拉斯矩阵可以分解为以下形式：

其中U中每一列的列向量为L的特征向量，中间的矩阵为主对角矩阵，主对角线上的元素分别为L的特征值。

从（6）可得，U为正交矩阵，即$U{U}^T=I$,故$U=U^{-1}$，所以上述特征分解可以写成一下形式：

1.3 谱分解（特征分解）

矩阵的特征分解，对角化，谱分解都是同一个概念，是指将矩阵分解为由其特征值和特征向量表示的矩阵乘积的方法。只有含有n个线性无关的特征向量的n维方阵才可以进行特征分解。
矩阵的谱分解（一）

1.4拉普拉斯算子

我的理解：
首先这里有一个函数$f(x,y,z)$
（1）梯度：对$f$中的x、y、z分别求偏导，然后相加

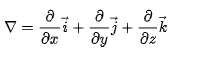
（2）散度：对于$f(x,y,z)$的梯度再求一次偏导，相加

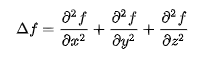
举个栗子
比如说一维：
梯度

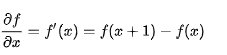
散度

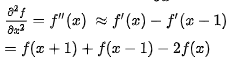
二维：

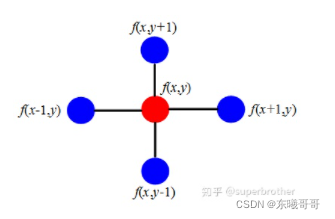
散度：

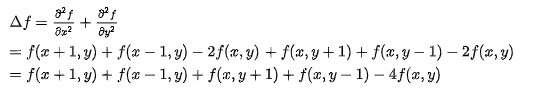
我们可以形象的理解成，拉普拉斯算子计算了周围点与中心点的梯度差。当$f(x,y)$受到扰动之后，其可能变为$f(x-1,y),f(x+1,y),f(x,y-1),f(x,y+1)$相邻的之一，拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益 （或者说是总变化）。

然后再对最后的式子进行一系《简单》推导，得到以下式子：

L为图的拉普拉斯矩阵，f为图向量矩阵。
很神奇！！！对不对！！！这里就把图联系上了~

送上解读链接，这个解读简直不要太详细好吧！！！：拉普拉斯矩阵与拉普拉斯算子

2. 傅里叶变换

这里一时半会解释不清，看完这个视频以后应该能理解了。（溜了溜了，有时间再来补这块知识）
参考：工科生用最快的时间理解傅立叶变换

---

五、GCN

这个视频的数学公式推导极其清晰明了，强推！！！（我在这就不推了，小伙伴们看视频的同时一定要拿笔和纸一起推一遍，数学的魅力啊~）图卷积神经网络（GCN）的数学原理详解

日后再补论文内容解读（其实看完上面这个视频，也差不多了嘿嘿）

---

总结

（1）卷积

（2）谱图理论

（3）傅里叶变换

（4）切比雪夫不等式

以上就是所需的相关知识，其实，我感觉都是基于数学的，数学万能啊，溜了溜了，得好好学数学呜呜呜！