概率论与数理统计(Probability & Statistics I)

---

概率论与数理统计(Probability & Statistics I)
概率论与数理统计(Probability & Statistics II)

Cheat Sheets:
Probability Cheatsheet v2.0
Probability Cheat Sheet

---

概率论的基本概念(The Basic Concept of Probability Theory)

• 基本概念
  概率论 (Theory of Probability)： 是一门揭示随机现象统计规律性的数学学科
  统计学 (Statistics)：是一门通过收集、整理、分析数据等手段以达到推断或预测考察对象本质或未来的学科.
  随机现象(random phenomenon)：个别实验结果呈现不确定性，大量重复实验又具有统计规律性的现象
  随机试验(random experiment)：对随机现象的观测
  样本和样本空间：试验的每一个结果称为一个样本(sample)，记为s
  所有可能出现的结果的集合称为样本空间 (sample space)，记为S
  随机事件(random event)：实际问题中，通常会关心随机试验一些特定的结果，它们是S的(可测)子集，称为事件(event)，通常用大写字母A, B,…表示。
  可列集(countable)：是指一个无穷集S，其元素可与自然数形成一一对应，因此可表为 S = { s 1 , s 2 , … } S=\{s_1,s_2,…\} S={s1​,s2​,…}

• 事件的关系与运算：设以下大写英文字母均为样本空间S中的事件
  $s\in A⟺$事件A发生
  $A\subset B⟺$指事件A必然导致事件B发生
  $A=B⟺A\subset B且B\subset A$
  $A\cup B⟺$称为事件A与B的和事件(union of events)，表示事件A与B至少有一个发生
  $A\cap B⟺$称为事件A与B的积事件(intersection of events)，表示事件A与B同时发生，也常记为AB
  $A-B⟺$称为事件A与B的差事件(difference of events)，表示事件A发生且B不发生
  $\bar{A}=S-A⟺$称为A的对立事件(complementary events)，表示事件A不发生
  特别的， $S$ 称为必然事件(certain event)，$\varnothing$称为不可能事件(impossible event)，单点集 { s } \{s\} {s} 称为基本事件(elementary event)
  若 $AB=\varnothing$，则称事件A与B互斥(mutually exclusive events)
  

交换律	$$\begin{gathered} A\cup B=B\cup A \\ A\cap B=B\cap A \end{gathered}$$
结合律	$$\begin{gathered} (A\cup B)\cup C=A\cup (B\cup C) \\ (A\cap B)\cap C=A\cap (B\cap C) \end{gathered}$$
分配律	$$\begin{gathered} A\cup (B\cap C)=(A\cup B)\cap (A\cup B) \\ A\cap (B\cup C)=(A\cap B)\cup (A\cap B) \end{gathered}$$
对偶律(De Morgan)	$$\begin{gathered} \overline{A\cup B}=\bar{A}\cap \bar{B},\overline{A\cap B}=\bar{A}\cup \bar{B} \\ \overline{\bigcup _{i=1}^n{A}_i}=\bigcap _{i=1}^n\overline{A_i},\overline{\bigcap _{i=1}^n{A}_i}=\bigcup _{i=1}^n\overline{A_i} \end{gathered}$$

• 频率(frequency)：$f_n(A)=\frac{n_A}{n}$
  其中 $n_A$ 是A发生的次数(频数），n 是总试验次数，称 $f_n(A)$ 为A在这 n 次试验中发生频率。
  频率的性质
  $1°0⩽f_n(A)⩽1$
  $2°f_n(S)=1$
  $3°f_n(\bigcup _{i=1}^k{A}_i)=\sum _{i=1}^k{f}_n(A_i),A_1,A_2,\cdots ,A_k$两两互斥

• 概率(probability)
  （统计性定义）当试验的次数增加时，随机事件A发生的频率的稳定值p称为概率，记为 $P(A)=p$
  （公理化定义）设随机试验对应的样本空间为S，定义P(A)满足以下性质，称P(A)为A的概率
  非负性：$P(A)⩾0$
  规范性：$P(S)=1$
  可列可加性：$A_i{A}_j=\varnothing ,(i\ne j)⟹P(\bigcup _{i=1}^{\infty }{A}_i)=\sum _{i=1}^{\infty }P(A_i)$
  概率的性质
  $1°P(\varnothing )=0$
  $2°P(A)=1-P(\bar{A})$
  $3°A_i{A}_j=\varnothing ,(i\ne j)⟹P(\bigcup _{i=1}^k{A}_i)=\sum _{i=1}^{k}P(A_i)$
  $4°A\subset B⟹P(B-A)=P(B)-P(A),P(B)⩾P(A)$
  $5°P(A\cup B)=P(A)+P(B)-P(AB)$

• 等可能概型(classical probability)：若试验满足，样本空间S中样本点有限(有限性)，出现每一个样本点的概率相等(等可能性)，称这种试验为等可能概型(或古典概型)。
  $P(A)=\frac{k}{n}$，其中k为A中所包含的样本点数，n为S中的样本点数。

• 几何概型(geometric probability)：（将等可能的原理进一步拓广）
  当样本空间 S 为 ${\mathbb{R}}^n$ 中的某个区域，如果没有特别的信息，则认为 ${\mathbb{R}}^n$ 中每一点的出现都是等可能的。因此如果事件A为S中的某个子区域，则认为A发生的概率为A与S 体积（或面积、长度）之比。

• 条件概率(conditional probability)：设A，B为事件，P(A)>0，定义$$P(B|A)=\frac{P(AB)}{P(A)}$$称为是A发生条件下B发生的概率
  条件概率空间：原样本空间的缩减 $S\to A$
  条件概率：原概率的限制 $P(\cdot )\to P(\cdot |A)$
  

• 条件概率性质：$P(\cdot |A)$ 是概率，具有概率的所有性质
  非负性：$P(B|A)⩾0$
  规范性：$P(S|A)=1$
  可列可加性：$B_i{B}_j=\varnothing ,(i\ne j)⟹P(\bigcup _{i=1}^{\infty }{B}_i|A)=\sum _{i=1}^{\infty }P(B_i|A)$
  乘法公式
  $P(AB)=P(A)P(B|A)=P(B)P(A|B)$
  $P(ABC)=P(A)P(B|A)P(C|AB)$
  $P(A_1{A}_2\cdots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1{A}_2)\cdots P(A_n|A_1{A}_2\cdots A_{n-1})$

• 事件独立性(independent)：设A，B是两随机事件，若 $P(AB)=P(A)P(B)$，称事件A，B独立
  $A$与$B$独立$⟺\bar{A}$与$B$独立$⟺A$与$\bar{B}$独立$⟺\bar{A}$与$\bar{B}$独立
  事件 A , B , C 独立，指下式同时成立。若只有前三个式子成立，称为两两独立。两两独立并不能决定三个事件独立。
  $\{\begin{array}{l}P(AB)=P(A)P(B)\\ P(BC)=P(C)P(C)\\ P(AC)=P(A)P(C)\\ P(ABC)=P(A)P(B)P(C)\end{array}$
  推广：事件 $A_1,A_2,\cdots ,A_n$ 相互独立，则对 $2⩽k⩽n$均有
  $P(A_{i_1}{A}_{i_2}\cdots A_{i_k})=\prod _{j=1}^{k}P(A_{i_j})$
  实际问题中,常常不是用定义去验证事件的独立性，而是由实际情形来判断其独立性.
  一旦确定事件是相互独立的，在计算概率时，尽可能转化为事件的乘积进行计算

• 全概率公式 (complete probability formula)：一个用于计算概率的公式，先化整为零，再聚零为整
  设 $B_1,\cdots ,B_n$ 是 $S$ 的一个划分，$A$为事件，则$$P(A)=\sum _{i=1}^{n}P(A|B_i)P(B_i)$$称 $S$ 的事件 $B_1,\cdots ,B_n$ 为一个划分，指它们满足
  $(1)\bigcup _{i=1}^n{B}_i=S(2)B_i{B}_j=\varnothing ,(i,j=1,2,\cdots ,n;i\ne j)$
  

• 贝叶斯公式(Bayes formula)：全概率公式通过划分 { B i ∣ i = 1 , ⋯   , n } \{B_i |i=1,\cdots,n\} {Bi​∣i=1,⋯,n} 来计算一个事件 $A$ 的概率，有时候需要弄清楚在A发生的条件下，每个 $B_i$ 发生的条件概率
  设 $B_1,\cdots ,B_n$ 是 $S$ 的一个划分，$A$为事件，则对于$i=1,\cdots ,n$，有$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum _{i=1}^{n}P(A|B_i)P(B_i)}$$

贝叶斯公式是关于随机事件$A$和$B$的条件概率和边缘概率的。

随机变量及其分布(Random Variable and Its Distribution)

随机变量(Random variable)

• 随机变量：设随机试验的样本空间为$S$，若$X=X(e)$为定义在 $S$上的实值单值函数，则称 $X(e)$ 为随机变量, 简写为 $X$
  
  说明：
  (1) 随机变量 $X(e):S\to R$ 为一映射，其自变量具有随机性；
  (2) 随机事件可以表示为 A = { e : X ( e ) ∈ I } = { X ∈ I } , I ⊂ R A=\{e : X(e)\in I\}=\{X\in I\}, I⊂ \R A={e:X(e)∈I}={X∈I},I⊂R
  如：将一枚均匀的硬币抛掷3次, 样本空间为
  S = { H H H , H H T , H T H , H T T , T H H , T H T , T T H , T T T } S=\{HHH,HHT,HTH,HTT,THH,THT,TTH,TTT\} S={HHH,HHT,HTH,HTT,THH,THT,TTH,TTT}
  若随机变量 $X$ 表示3次中出现正面(H)的次数, 则
  随机事件 A={正面出现了一次}={X=1}
  随机事件 B={3次出现的情况相同}={X=0或3}
  随机事件 C={正面至少出现了一次}={$X⩾1$}
  (3) 对于 $i\ne j$，则必有 { X = i } ∩ { X = j } = ∅ \{X=i\}∩\{X=j\}=\varnothing {X=i}∩{X=j}=∅
  (4) 一般用大写英文字母 X,Y,Z 或希腊字母 $\xi ,\eta$ 等来表示随机变量

离散型随机变量及分布律(Discrete random variable & distribution law)

• 定义：若随机变量X的取值为有限个或可数 , 则称 X 为离散(discrete)型随机变量。
• 分布律 (distribution law)：离散随机变量在各特定取值上的概率，也称概率质量函数(probability mass function, PMF)
  P { X = x k } = p k ,   k = 1 , 2 , ⋯ P\{X=x_k\}=p_k,\ k=1,2,\cdots P{X=xk​}=pk​, k=1,2,⋯

$X$	$x_1{x}_2\cdots x_k\cdots$	随机变量的所有可能取值
$P$	$p_1{p}_2\cdots p_k\cdots$	取每个可能取值相应的概率

分布律满足：$p_k⩾0,\sum _{k=1}^{+\infty }{p}_k=1$

• 几种重要的离散型随机变量
  0-1分布：随机变量X只能取0和1，又称两点分布或伯努利(Bernoulli)分布，记为$X\sim B(1,p)$
  P { X = k } = p k ( 1 − p ) 1 − k ,   k = 0 , 1 P\{X=k\}=p^k(1-p)^{1-k},\ k=0,1 P{X=k}=pk(1−p)1−k, k=0,1
  常用它来表示两个状态的问题（即随机试验的结果只有两个，称为伯努利试验）：
  S = { s 1 , s 2 } , X ( s 1 ) = 1 , X ( s 2 ) = 0 S=\{s_1,s_2\},\quad X(s_1)=1,X(s_2)=0 S={s1​,s2​},X(s1​)=1,X(s2​)=0
  应用：检查产品的质量是否合格；对新生婴儿的性别进行登记
  二项分布（Binomial）：将上述伯努利试验独立地做n次，称为n重伯努利试验。设状态 $s_1,s_2$ 在每次试验中出现的概率是不变的。设X为n次试验中状态$s_1$出现的次数，则X的取值为$0,1,\cdots ,n$ ，而 $X=k$ 的不同情况共有 $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ 种，他们是互斥的，于是 P { X = k } = ∁ n k p k ( 1 − p ) n − k , k = 1 , 2 , ⋯   , n P\{X=k\}=∁^k_np^k(1-p)^{n-k},k=1,2,\cdots,n P{X=k}=∁nk​pk(1−p)n−k,k=1,2,⋯,n称具有上述分布律的随机变量为服从参数为n, p的二项分布, 记为$X\sim B(n,p)$
  应用：有放回抽样
  泊松分布（Poisson）：若的概率分布律为 P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2 , ⋯ P\{X=k\}=\dfrac{λ^ke^{-λ}}{k!},k=0,1,2,\cdots P{X=k}=k!λke−λ​,k=0,1,2,⋯其中$\lambda >0$，就称服从参数为$\lambda$的泊松分布，记为 $X\sim \pi (\lambda )$ 或 $X\sim P(\lambda )$
  应用：一段时间内物理试验仪器捕获的粒子数；一本书中的错字数；
  几何分布（geometric）：在重复多次的伯努利试验中, 试验进行到某种结果首次出现为止, 此时X 的分布律为 P { X = k } = p ( 1 − p ) k − 1 , k = 1 , 2 , ⋯ P\{X=k\}=p(1-p)^{k-1},k=1,2,\cdots P{X=k}=p(1−p)k−1,k=1,2,⋯X 的这种分布由此等比数列(几何级数)表达, 故称为参数为p的几何分布。记为 $X\sim \text{Geom}(p)$

连续型随机变量及概率密度(Continuous random variable & probability density)

• 分布函数(distribution function)：对于随机变量X，定义函数 F ( x ) = P { X ⩽ x } , ∀ x ∈ R F(x)=P\{X⩽ x\},∀ x\in \R F(x)=P{X⩽x},∀x∈R 称为X的累积分布函数(cumulative distribution function ,CDF) 。
  任何随机变量都有相应的分布函数，分布函数可以给出随机变量落入任意一个范围的可能性。
  一般地，离散型随机变量的分布函数为阶梯函数。
  分布函数的基本性质：
  (1) $0⩽F(x)⩽1$
  (2) $F(x)$是单调不减函数
  (3) $$\begin{gathered} F(-\infty )=\underset{x\to -\infty }{\lim }F(x)=0 \\ F(+\infty )=\underset{x\to +\infty }{\lim }F(x)=1 \end{gathered}$$
  (4) $F(x)$是右连续函数，即$F(x)=F(x+0)=\underset{y\to x^{+}}{\lim }F(y)$

• 连续型随机变量(continuous random variable)：设随机变量 X 的分布函数 F(x) 可表成其中$$F(x)={\int }_{-\infty }^{x}f(t)\mathrm{d}t$$其中 $f(x)⩾0$, 则称X是连续型随机变量，$f(x)$ 称为是 X 的概率密度函数（probability density function ,PDF），简称概率密度。
  概率密度的性质：
  (1) $f(x)⩾0$
  (2) ${\int }_{-\infty }^{+\infty }f(t)\mathrm{d}t=1$
  (3) ∀ x 1 < x 2 , P { x 1 < X ⩽ x 2 } = F ( X 2 ) − F ( x 1 ) = ∫ x 1 x 2 f ( t ) d t ∀ x_1<x_2,P\{x_1<X⩽ x_2\}=F(X_2)-F(x_1)=\int_{x_1}^{x_2}f(t)\mathrm{d}t ∀x1​<x2​,P{x1​<X⩽x2​}=F(X2​)−F(x1​)=∫x1​x2​​f(t)dt
  (4) 在$F(x)$的连续点，$f(x)=F^{\prime }(x)$
  几种重要的连续型分布
  均匀分布(uniformly)：若X的概率密度函数为$$f(x)=\{\begin{array}{l}\frac{1}{b-a},x\in [a,b]\\ 0,x\in (-\infty ,a)\cup (b,+\infty )\end{array}$$其中$a<b$，就称X服从$[a,b]$上的均匀分布，记为$X\sim U(a,b)$
  分布函数为$F(x)=\{\begin{array}{l}0,x<a\\ \frac{x-a}{b-a},x\in [a,b]\\ 1,x>b\end{array}$
  均匀分布具有等可能性：取值的概率只与小区间的长度有关，而与其位置无关。
  
  指数分布(exponential)：若X的概率密度函数为$$f(x)=\{\begin{array}{l}\frac{1}{\theta }{e}^{-x/\theta },x>0\\ 0,x⩽0\end{array}$$其中$\theta >0$，就称X服从参数$\theta$的指数分布，记为$X\sim E(\theta )$ 或 $X\sim Exp(\theta )$
  分布函数为$F(x)=\{\begin{array}{ll}1-e^{-x/\theta },& x>0\\ 0,& x⩽0\end{array}$
  指数分布具有无记忆性：对于 t 0 > 0 , t > 0 , P { X > t 0 + t ∣ X > t 0 } = P { X > t } t_0>0,t>0,P\{X>t_0+t|X>t_0\}=P\{X>t\} t0​>0,t>0,P{X>t0​+t∣X>t0​}=P{X>t}
  应用：通常用来描述生命周期；表示独立随机事件发生的时间间隔；
  正态分布(normal distribution)：连续型随机变量 X 如果有如下形式的概率密度函数$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}(\mu \in \mathbb{R},\sigma >0)$$则称 X 服从参数为 $(\mu ,{\sigma }^2)$ 的正态分布 或高斯分布，记为 $X\sim N(\mu ,{\sigma }^2)$
  特征：(1) $f(x)$关于$x=\mu$对称， $f_{\max }=f(\mu )=\frac{1}{\sqrt{2\pi }\sigma }$
  (2) 当$x⩽\mu$时，$f(x)$是严格单调递增函数
  (3) $x=\mu \pm \sigma$是$f(x)$的拐点
  (4) $\underset{|x-\mu |\to +\infty }{\lim }f(x)=0$
  两个参数的含义：
  (1) 当固定 σ 改变 μ 的大小时，图形的形状不变，只是沿着 x 轴作平移变换；
  μ 称为位置参数，决定对称轴位置
  (2) 当固定 μ 改变 σ 的大小时，图形的对称轴不变，而形状在改变， σ 越小图形越高越瘦，σ 越大图形越矮越胖；
  σ 称为尺度参数，决定曲线分散程度
  
  应用：测量值与实际值的误差；分子热运动时每个分子的运动速率；

若 $X\sim N(\mu ,{\sigma }^2),X$的分布函数 F ( x ) = P { X ⩽ x } = ∫ − ∞ x f ( t ) d t F(x)=P\{X⩽ x\}=\int_{-∞}^{x}f(t)\mathrm{d}t F(x)=P{X⩽x}=∫−∞x​f(t)dt一般无解析解。

标准正态分布（standard normal distribution）：若 $Z\sim N(0,1)$ 称 Z 服从标准正态分布
Z 的概率密度函数： $\varphi (z)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{z^2}{2}}$
Z 的分布函数：$\Phi (z)={\int }_{-\infty }^z\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}\mathrm{d}t$
重要性质：关于 轴的对称 $\Phi (-z_0)=1-\Phi (z_0)$
当 $X\sim N(\mu ,{\sigma }^2)$时，$\frac{X-\mu }{\sigma }\sim N(0,1)$，由此可知
∀ a ∈ R , F X ( a ) = P { X ⩽ a } = P { X − μ σ ⩽ a − μ σ } = Φ ( a − μ σ ) ∀ a\in\R,F_X(a)=P\{X⩽ a\}=P\{\frac{X-μ}{σ} ⩽ \frac{a-μ}{σ}\}=Φ(\frac{a-μ}{σ}) ∀a∈R,FX​(a)=P{X⩽a}=P{σX−μ​⩽σa−μ​}=Φ(σa−μ​)

常采用的3σ原则： P { ∣ X − μ ∣ ⩽ 3 σ } ≈ 0.9974 P\{|X-μ|⩽ 3σ\}\approx 0.9974 P{∣X−μ∣⩽3σ}≈0.9974

随机变量的函数(Random variable function)

有时我们关心的随机变量不是直接观测得到的随机变量，而是它的函数。
如要得到一个圆的面积 Y，总是测量其半径，半径的测量值可看作随机变量X，若 $X\sim N(\mu ,{\sigma }^2)$，则 Y 的分布是什么？

一般地，设 X 为一随机变量, 分布已知.。$Y=g(X)$, 其中 g 为一确定的实函数, 要求 Y 的分布。仍讨论离散型与连续型两种情况：
(1) 设 X 为离散型，求 Y 的分布律
先逐个算出 Y 的取值 $g(x_1),g(x_2),\cdots$， 每个$g(x_k)$对应的概率为$p_k$；再合并所有相同的 $g(x_k)$, 并将对应的 $p_k$ 相加。
(2) 设 X 为连续型随机变量, 具有概率密度 $f_X(x)$, 又设$Y=g(X)$亦为连续型随机变量，求其概率密度 $f_Y(y)$
先求分布函数 F Y ( y ) = P { Y ⩽ y } = P { g ( X ) ⩽ y } = ∫ D f X ( x ) d x F_Y(y)=P\{Y⩽ y\}=P\{g(X)⩽ y\}=\int_Df_X(x)\mathrm{d}x FY​(y)=P{Y⩽y}=P{g(X)⩽y}=∫D​fX​(x)dx，其中积分区域 D = { x ∣ g ( x ) ⩽ y } D=\{x|g(x)⩽ y \} D={x∣g(x)⩽y}，然后对分布函数求导, 得到概率概率密度。

定理：设随机变量 $X\sim F_X(x),x\in \mathbb{R},Y=g(X),g^{\prime }(X)>0或g^{\prime }(X)<0$，则具有概率密度为$$f_Y(y)=\{\begin{array}{l}{f}_X[h(y)]\cdot |h^{\prime }(y)|,y\in [a,b]\\ 0,y\in (-\infty ,a)\cup (b,+\infty )\end{array}$$其中 $[a,b]$是 Y 的取值范围，h是g 的反函数，即$h(y)=x$

一般地，若随机变量 $X\sim N(\mu ,{\sigma }^2)$
则 $Y=aX+b⟹Y\sim N(a\mu +b,a^2{\sigma }^2)$

多维随机变量及其分布(Multiple Random Variable and Its Distribution)

二维随机变量(Two-dimensional random variable)

• 二维随机变量：设E是一个随机试验，样本空间$S=e$；设$X=X(e)$和$Y=Y(e)$是定义在S上的随机变量，由它们构成的向量$(X,Y)$称为二维随机向量或二维随机变量。
  二维随机变量分布函数：设 $(X,Y)$ 是二维随机变量，对于任意 $(x,y)\in {\mathbb{R}}^2$，二维函数 F ( x , y ) = P { { X ⩽ x } ∩ { Y ⩽ y } } ≜ P { X ⩽ x , Y ⩽ y } F(x,y)=P\{\{X⩽ x\}∩\{Y⩽ y\}\}\triangleq P\{X⩽ x,Y⩽ y\} F(x,y)=P{{X⩽x}∩{Y⩽y}}≜P{X⩽x,Y⩽y}称为二维随机变量的联合分布函数 ( joint distribution function,JDF)。
  性质：
  1。$F(x,y)$为单调不减函数
  2。$$\begin{gathered} \forall x,y,0⩽F(x,y)⩽1, \\ F(+\infty ,+\infty )=1,F(-\infty ,y)=F(x,-\infty )=F(-\infty ,-\infty )=0 \end{gathered}$$
  3。$F(x,y)$关于$x,y$右连续，即：$\underset{ϵ\to 0^{+}}{\lim }F(x+ϵ,y)=\underset{ϵ\to 0^{+}}{\lim }F(x,y+ϵ)=F(x,y)$
  4。 x 1 < x 2 , y 1 < y 2    ⟹    P { x 1 < X ⩽ x 2 , y 1 < Y ⩽ y 2 } = F ( x 2 , y 2 ) − F ( x 1 , y 2 ) − F ( x 2 , y 1 ) + F ( x 1 , y 1 ) ⩾ 0 x_1<x_2,y_1<y_2\\ \implies P\{x_1<X ⩽ x_2,y_1<Y ⩽ y_2\}=F(x_2,y_2)-F(x_1,y_2)-F(x_2,y_1)+F(x_1,y_1) ⩾ 0 x1​<x2​,y1​<y2​⟹P{x1​<X⩽x2​,y1​<Y⩽y2​}=F(x2​,y2​)−F(x1​,y2​)−F(x2​,y1​)+F(x1​,y1​)⩾0
  

• 二维离散型随机变量：若二维随机变量$(X,Y)$全部可能取到的不同值是有限对或可列无限对，则称$(X,Y)$是二维离散型随机变量。
  联合分布律：设$(X,Y)$所有可能取值为$(X_i,Y_i)$，称 P { X = x i , Y = y j } = p i j , i , j = 1 , 2 , ⋯ P\{X=x_i,Y=y_j\}=p_{ij},i,j=1,2,\cdots P{X=xi​,Y=yj​}=pij​,i,j=1,2,⋯为二维离散型随机变量$(X,Y)$的联合（概率）分布律。
  联合分布律的性质：$(1)0⩽p_{ij}⩽1;(2)\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{p}_{ij}=1$

• 二维连续型随机变量：设二维随机变量 $(X,Y)$ 的分布函数 $F(x,y),\exists f(x,y)⩾0,\forall (x,y)\in {\mathbb{R}}^2$有$$F(x,y)={\int }_{-\infty }^x{\int }_{-\infty }^{y}f(u,v)\mathrm{d}u\mathrm{d}v$$则称 $(X,Y)$ 为二维连续型随机变量，$f(x,y)$ 称为是 $(X,Y)$ 的联合概率密度(函数)。
  概率密度的性质：
  1。$f(x,y)⩾0$
  2。${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(x,y)\mathrm{d}x\mathrm{d}y=1$
  3。在 $f(x,y)$ 的连续点处，有 $\frac{\partial F(x,y)}{\partial x\partial y}=f(x,y)$
  4。对于任何${\mathbb{R}}^2$上的区域G, 有 P { ( X , Y ) ∈ G } = ∬ G f ( u , v ) d u d v P\{(X,Y)\in G\}=\iint\limits_G f(u,v)\mathrm{d}u\mathrm{d}v P{(X,Y)∈G}=G∬​f(u,v)dudv
  

边缘分布(Marginal distribution)

边缘分布律：对分布律为 P { X = x i , Y = y j } = p i j P\{X=x_i,Y=y_j\}=p_{ij} P{X=xi​,Y=yj​}=pij​ 的二维离散型随机变量
P { X = x i } = P { X = x i , ⋃ j = 1 ∞ { Y = y j } } = ∑ j = 1 ∞ p i j ≜ p i ∙ \displaystyle P\{X=x_i\}=P\{X=x_i,\bigcup^{∞}_{j=1}\{Y=y_j\}\}=\sum_{j=1}^{∞}p_{ij}\triangleq p_{i\bullet} P{X=xi​}=P{X=xi​,j=1⋃∞​{Y=yj​}}=j=1∑∞​pij​≜pi∙​
同理， P { Y = y j } = P { ⋃ i = 1 ∞ { X = x i } , Y = y j } = ∑ i = 1 ∞ p i j ≜ p ∙ j \displaystyle P\{Y=y_j\}=P\{\bigcup^{∞}_{i=1}\{X=x_i\},Y=y_j\}=\sum_{i=1}^{∞}p_{ij}\triangleq p_{\bullet j} P{Y=yj​}=P{i=1⋃∞​{X=xi​},Y=yj​}=i=1∑∞​pij​≜p∙j​

X / Y y 1 y 2 ⋯ y j ⋯ P { X = x i } x 1 p 11 p 12 ⋯ p 1 j ⋯ p 1 ∙ x 2 p 21 p 22 ⋯ p 2 j ⋯ p 2 ∙ ⋮ ⋯ ⋯ ⋯ ⋮ x i p i 1 p i 2 ⋯ p i j ⋯ p i ∙ ⋮ ⋯ ⋯ ⋯ ⋮ P { Y = y j } p ∙ 1 p ∙ 2 ⋯ p ∙ j ⋯ 1 \begin{array}{c|ccccc|c} X/Y &y_1&y_2&\cdots&y_j&\cdots &P\{X=x_i\} \\ \hline x_1 &p_{11}&p_{12}&\cdots&p_{1j}&\cdots &p_{1 \bullet} \\ x_2 &p_{21}&p_{22}&\cdots&p_{2j}&\cdots &p_{2 \bullet} \\ \vdots &\cdots&&\cdots&&\cdots &\vdots \\ x_i&p_{i1}&p_{i2}&\cdots&p_{ij}&\cdots &p_{i \bullet} \\ \vdots &\cdots&&\cdots&&\cdots &\vdots \\ \hline P\{Y=y_j\} &p_{\bullet 1}&p_{\bullet 2}&\cdots&p_{\bullet j}&\cdots &1 \end{array} X/Yx1​x2​⋮xi​⋮P{Y=yj​}​y1​p11​p21​⋯pi1​⋯p∙1​​y2​p12​p22​pi2​p∙2​​⋯⋯⋯⋯⋯⋯⋯​yj​p1j​p2j​pij​p∙j​​⋯⋯⋯⋯⋯⋯⋯​P{X=xi​}p1∙​p2∙​⋮pi∙​⋮1​​

边缘概率密度：对概率密度为$f(x,y)$的二维连续型随机变量
$$\begin{gathered} f_X(x)={\int }_{-\infty }^{+\infty }f(x,y)\mathrm{d}y \\ {f}_Y(y)={\int }_{-\infty }^{+\infty }f(x,y)\mathrm{d}x \end{gathered}$$

边缘分布函数：可以由$(X,Y)$的分布函数所确定
F X ( x ) ≜ P { X ⩽ x , Y < + ∞ } = F ( x , + ∞ ) = lim ⁡ y → + ∞ F ( x , y ) F_X(x)\triangleq P\{X ⩽ x,Y<+∞\}=F(x,+∞)=\lim\limits_{y\to +∞}F(x,y) FX​(x)≜P{X⩽x,Y<+∞}=F(x,+∞)=y→+∞lim​F(x,y)
F Y ( y ) ≜ P { X < + ∞ , Y ⩽ y } = F ( + ∞ , y ) = lim ⁡ x → + ∞ F ( x , y ) F_Y(y)\triangleq P\{X<+∞,Y ⩽ y\}=F(+∞,y)=\lim\limits_{x\to +∞}F(x,y) FY​(y)≜P{X<+∞,Y⩽y}=F(+∞,y)=x→+∞lim​F(x,y)

相互独立(mutual independence)：$\forall x,y,F(x,y)=F_X(x)F_Y(y)$称随机变量X ,Y相互独立。
二维离散型：$⟺p_{ij}=p_{i\bullet }{p}_{\bullet j}$
二维连续型：$⟺f(x,y)=f_X(x)f_Y(y)$

条件分布(Conditional distribution)

条件分布(conditional distribution)：对二维离散型随机变量 $(X,Y)$
P { X = x i ∣ Y = y j } = P { X = x i , Y = y j } P { Y = y j } = p i j p ∙ j P\{X=x_i|Y=y_j\}=\dfrac{P\{X=x_i,Y=y_j\}}{P\{Y=y_j\}}=\dfrac{p_{ij}}{p_{\bullet j}} P{X=xi​∣Y=yj​}=P{Y=yj​}P{X=xi​,Y=yj​}​=p∙j​pij​​
同理， P { Y = y j ∣ X = x i } = P { X = x i , Y = y j } P { X = x i } = p i j p i ∙ P\{Y=y_j|X=x_i\}=\dfrac{P\{X=x_i,Y=y_j\}}{P\{X=x_i\}}=\dfrac{p_{ij}}{p_{i \bullet}} P{Y=yj​∣X=xi​}=P{X=xi​}P{X=xi​,Y=yj​}​=pi∙​pij​​

条件概率密度：对二维连续型随机变量 $(X,Y)$
当 $Y=y$时，X的条件概率密度$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$
同理 $f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}$

条件分布函数：
F X ∣ Y ( x ∣ y ) = P { X ⩽ x ∣ Y = y } = { P { X ⩽ x , Y = y } P { Y = y } , P { Y = y } > 0 , 即 Y 为 离 散 型 随 机 变 量 lim ⁡ ϵ → 0 + P { X ⩽ x , y < Y ⩽ y + ϵ } P { y < Y ⩽ y + ϵ } , P { Y = y } = 0 , 即 Y 为 连 续 型 随 机 变 量 F_{X|Y}(x|y)=P\{X⩽ x|Y=y\}= \\ \begin{cases} \dfrac{P\{X⩽ x,Y=y\}}{P\{Y=y\}}, & P\{Y=y\}>0,即Y为离散型随机变量 \\ \\ \lim\limits_{ϵ\to 0^+}\dfrac{P\{X⩽ x,y<Y⩽ y+ϵ\}}{P\{y<Y⩽ y+ϵ\}},&P\{Y=y\}=0,即Y为连续型随机变量 \end{cases} FX∣Y​(x∣y)=P{X⩽x∣Y=y}=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​P{Y=y}P{X⩽x,Y=y}​,ϵ→0+lim​P{y<Y⩽y+ϵ}P{X⩽x,y<Y⩽y+ϵ}​,​P{Y=y}>0,即Y为离散型随机变量P{Y=y}=0,即Y为连续型随机变量​

常见的二维随机变量分布(Usual two-dimensional distribution of random variables)

二维均匀分布：概率密度函数$f(x,y)=\{\begin{array}{ll}1/A,& (x,y)\in D\\ 0,& (x,y)\notin D\end{array}，其中A为D的面积$

二维正态分布：
(1) 设 $Z_1,Z_2$ 为独立同分布 $N(0,1)$ 的随机变量，则 $Z_1,Z_2$ 的联合密度函数为 $f(z_1,z_2)=\frac{1}{2\pi }{e}^{-\frac{1}{2}(z_1^2+z_2^2)}$
(2) 作变换，令$\{\begin{array}{l}X={\sigma }_1{Z}_1+{\mu }_1\\ Y={\sigma }_2(\rho Z_1+\sqrt{1-{\rho }^2}{Z}_2)+{\mu }_2\end{array}({\sigma }_1,{\sigma }_2>0,|\rho |<1)$
则称 $(X,Y)$ 服从参数为 $({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,\rho )$ 的二维正态分布，记为 $(X,Y)\sim N({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,\rho )$
变换可写成矩阵式：$\left(\begin{array}{c}X\\ Y\end{array}\right)=A\left(\begin{array}{c}{Z}_1\\ Z_2\end{array}\right)+\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right)$
其中 $A=\left(\begin{array}{cc}{\sigma }_1& 0\\ {\sigma }_2\rho & {\sigma }_2\sqrt{1-{\rho }^2}\end{array}\right)$，于是 $\left(\begin{array}{c}{Z}_1\\ Z_2\end{array}\right)=A^{-1}\left(\begin{array}{c}X-{\mu }_1\\ Y-{\mu }_2\end{array}\right)$
将此式代入 $Z_1,Z_2$ 的联合密度式，并注意到此变换中雅可比行列式为
$|J|=\det A^{-1}=\frac{1}{{\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}}$
即得 $(X,Y)$ 的联合密度 $f(x,y)$ (过于复杂，就不写了！)

由定义知若$\rho =0$ , 则 $X={\sigma }_1{Z}_1+{\mu }_1,Y={\sigma }_2{Z}_2+{\mu }_2$，即 X 与 Y 独立。从密度函数看，X 与Y 地位是对称的，决定了它们的分布特点是一致的.
二维正态的定义的特点使得许多分布规律的计算十分简单。

边缘概率密度：因 $X={\sigma }_1{Z}_1+{\mu }_1$，故 $X\sim N({\mu }_1,{\sigma }_1^2)$，由对称性可知$Y\sim N({\mu }_2,{\sigma }_2^2)$，两个边缘分布均与ρ无关
条件概率密度：由于$Z_1=\frac{x-{\mu }_1}{{\sigma }_1}$，故$Y{|}_{X=x}\sim N(\frac{{\sigma }_2\rho }{{\sigma }_1}(x-{\mu }_1),{\sigma }_2^2(1-{\rho }^2))$
由对称性可知$X{|}_{Y=y}\sim N(\frac{{\sigma }_1\rho }{{\sigma }_2}(y-{\mu }_2),{\sigma }_1^2(1-{\rho }^2))$

两个随机变量的函数的分布(The distribution of two random-variables functions)

二维离散：设二维离散型随机变量$(X,Y)$具有分布律 P { X = x i , Y = y j } = p i j P\{X=x_i,Y=y_j\}=p_{ij} P{X=xi​,Y=yj​}=pij​
(1) 若$U=u(X,Y)$，求$U$的分布律
先确定$U$的取值$u_i$，再找出 P { U = u i } = P { ( X , Y ) ∈ D } P\{U=u_i\}=P\{(X,Y)\in D\} P{U=ui​}=P{(X,Y)∈D}计算分布律
(2) 若$U=u(X,Y),V=v(X,Y)$，求$(U,V)$的分布律
先确定$(U,V)$的取值$(u_i,v_i)$，再找出 P { U = u i , V = v i } = P { ( X , Y ) ∈ D } P\{U=u_i,V=v_i\}=P\{(X,Y)\in D\} P{U=ui​,V=vi​}=P{(X,Y)∈D}计算分布律

二维连续：设二维连续型随机变量$(X,Y)$具有概率密度 $f(x,y)$
(1) 若$Z=g(X,Y)$，求$Z$的分布函数或概率密度
先求Z的分布函数 F Z ( z ) = P { Z ⩽ z } = P { g ( X , Y ) ⩽ z } = ∬ g ( x , y ) ⩽ z f ( x , y ) d x d y \displaystyle F_Z(z)=P\{Z⩽ z\}=P\{g(X,Y)⩽ z\}=\iint\limits_{g(x,y)⩽ z}f(x,y)\mathrm{d}x\mathrm{d}y FZ​(z)=P{Z⩽z}=P{g(X,Y)⩽z}=g(x,y)⩽z∬​f(x,y)dxdy
再求导得到密度函数 $f_Z(z)=F_Z^{\prime }(z)$
(2) 若 $(U,V)$为$(X,Y)$的一个变换，并设变换的雅可比矩阵存在, 且行列式不为零，求$(U,V)$的概率密度
因$(U,V)$为$(X,Y)$的一个变换，故可设 $X=x(U,V),Y=y(U,V)$
又$(U,V)$的分布函数可表为 G ( u , v ) = P { U ⩽ u , V ⩽ v } = ∬ U ⩽ u , V ⩽ v f ( x , y ) d x d y \displaystyle G(u,v)=P\{U⩽ u,V⩽ v\}=\iint\limits_{U⩽ u,V⩽ v}f(x,y)\mathrm{d}x\mathrm{d}y G(u,v)=P{U⩽u,V⩽v}=U⩽u,V⩽v∬​f(x,y)dxdy
将上述变换用于积分，即得
$G(u,v)={\int }_{-\infty }^u{\int }_{-\infty }^{v}f[x(s,t),y(s,t)]|J(s,t)|\mathrm{d}s\mathrm{d}t$
对上式求两阶偏导，即得
$g(u,v)=\frac{{\partial }^{2}G(u,v)}{\partial u\partial v}=f[x(s,t),y(s,t)]|J(s,t)|$

连续型随机变量$Z=X+Y$的分布
$F_Z(z)={\int }_{-\infty }^z{f}_Z(u)\mathrm{d}u$
$f_Z(z)={\int }_{-\infty }^{+\infty }f(z-y,y)\mathrm{d}y={\int }_{-\infty }^{+\infty }f(x,z-x)\mathrm{d}x$
特别, 若X与Y 独立, 则有
$f_Z(z)={\int }_{-\infty }^{+\infty }{f}_X(z-y)f_Y(y)\mathrm{d}y={\int }_{-\infty }^{+\infty }{f}_Y(z-x)f_X(x)\mathrm{d}x$
称 $f_Z$ 为 $f_X$ 与 $f_Y$ 的卷积，记为 $f_Z=f_X\ast f_Y$

对于一般的两独立正态随机变量 $X\sim N({\mu }_1,{\sigma }_1^2),Y\sim N({\mu }_2,{\sigma }_2^2)⟹Z=X+Y\sim N({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$

独立的离散型变量的和分布
(1) $X_1,X_2,\cdots ,X_n$独立且服从分布$B(1,p)$，则$X_1+X_2+\cdots +X_n\sim B(n,p)$
(2) $X_1\sim B(n_1,p),X_2\sim B(n_2,p)$，且两者独立，则$X_1+X_2\sim B(n_1+n_2,p)$
(3) $X_1\sim \pi ({\theta }_1),X_2\sim \pi ({\theta }_2)$，且两者独立，则$X_1+X_2\sim \pi (1/{\theta }_1+1/{\theta }_2)$

连续型随机变量$Z=X/Y$的分布
$f_Z(z)=\{\begin{array}{ll}(1+z{)}^{-2},& z>0\\ 0,& z⩽0\end{array}$

极值分布(extreme-value distribution)：设 X, Y 独立，分别有分布函数 $F_X(x),F_Y(y)$
max ⁡ { X , Y } \max\{X, Y\} max{X,Y}的分布函数 $F_{max}(z)=F_X(x)F_Y(y)$
min ⁡ { X , Y } \min\{X, Y\} min{X,Y}的分布函数 $F_{min}(z)=1-(1-F_X(x))(1-F_Y(y))$

上述结论容易推广到 n 个随机变量：即设 $X_i$ 的分布函数分别为 $F_i(x_i),i=1,\cdots ,n$，且相互独立。则 max ⁡ { X 1 , ⋯   , X n } , min ⁡ { X 1 , ⋯   , X n } \max\{X_1,\cdots,X_n\}, \min\{X_1,\cdots,X_n\} max{X1​,⋯,Xn​},min{X1​,⋯,Xn​}的分布函数：
$F_{\max }(z)=\prod _{i=1}^n{F}_i(z);F_{\min }(z)=1-\prod _{i=1}^n(1-F_i(z))$

随机变量的数字特征(Numerical Characteristics)

期望(Expectation)

数学期望(mathematical expectation)：设离散型随机变量 X的分布律为 P { X = x k } = p k P\{X=x_k\}=p_k P{X=xk​}=pk​
事件的平均值 $\bar{x}=\frac{1}{n}\sum _k{x}_k{n}_k=\sum _k{x}_k{f}_k$，其中$f_k$为事件 { X = x k } \{X=x_k\} {X=xk​}发生的频率，由第一章可知当$n\to \infty ,f_k\to p_k$，因此$\bar{x}$的稳定值为$\sum _k{x}_k{p}_k$，由此
若级数$$E(X)=\sum _{k=1}^{\infty }{x}_k{p}_k$$绝对收敛，则称 $E(X)$为随机变量 $X$的数学期望，简称期望，又称均值(mean)
连续型随机变量 $X$的密度函数为 $f(x)$，期望定义为$$E(X)={\int }_{-\infty }^{+\infty }xf(x)\mathrm{d}x$$
期望的物理意义：x 轴上一根线密度为 f(x) 的细棒的质心坐标
Y=g(X) 的数学期望
(1) 离散情形：$E(Y)=E(g(X))=\sum _{k=1}^{\infty }g(x_k)p_k$
(2) 连续情形：$E(Y)=E(g(X))={\int }_{-\infty }^{+\infty }g(x)f(x)\mathrm{d}x$
Z=h(X,Y) 的数学期望
(1) 离散情形：$E(Z)=E(h(X,Y))=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }h(x_i,y_j)p_{ij}$
(2) 连续情形：$E(Z)=E(h(X,Y))={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }h(x,y)f(x,y)\mathrm{d}x\mathrm{d}y$
特别的，$E(X)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }xf(x,y)\mathrm{d}x\mathrm{d}y$
$E(Y)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }yf(x,y)\mathrm{d}x\mathrm{d}y$
期望的性质（c为常数）
(1) $E(c)=c$
(2) $E(cX)=cE(X)$
(3) $E(X+Y)=E(X)+E(Y)$
(4) 设$X,Y$相互独立，$E(XY)=E(X)E(Y)$

方差和变异系数(Variance and CV)

方差(variance)：设X是一个随机变量$$D(X)=Var(X)=E[(X-E(X){)}^2]$$叫做X的方差。将$\sigma (X)=\sqrt{D(X)}$为 X 的标准差(standard deviation)或均方差。方差和标准差刻画了 X取值的波动性，是衡量取值分散程度的数字特征。
方差的计算
特别的，当$g(X)=(X-E(X){)}^2,D(X)=E(g(X))$
利用期望的性质，$D(X)=E(X^2)-[E(X){]}^2$
方差的性质（c为常数）
(1) $D(c)=0$
(2) $D(cX)=c^{2}D(X)$
(3) $D(X+Y)=D(X)+D(Y)+2E[(X-E(X))(Y-E(Y))]$
当$X,Y$相互独立，$D(X+Y)=D(X)+D(Y)$
(4) 切比雪夫(Chebyshev)不等式，设 E ( X ) = μ , D ( X ) = σ 2 , P { ∣ X − μ ∣ ⩾ ϵ } ⩽ σ 2 ϵ 2 E(X)=μ,D(X)=σ^2,P\{|X-μ|⩾ ϵ\}⩽ \dfrac{σ^2}{ϵ^2} E(X)=μ,D(X)=σ2,P{∣X−μ∣⩾ϵ}⩽ϵ2σ2​
结果分析，将切比雪夫不等式变形为 P { ∣ X − μ ∣ < ϵ } > 1 − σ 2 ϵ 2 P\{|X-μ|< ϵ\}>1-\dfrac{σ^2}{ϵ^2} P{∣X−μ∣<ϵ}>1−ϵ2σ2​，取$ϵ=3\sigma$则有 P { ∣ X − μ ∣ < 3 σ } > 1 − 1 9 ≈ 88.0 % P\{|X-μ|< 3σ\}>1-\frac{1}{9}\approx 88.0\% P{∣X−μ∣<3σ}>1−91​≈88.0%，即随机变量有近90%的可能性落在区间$(\mu -3\sigma ,\mu +3\sigma )$内。

变异系数(Coefficient of Variance,CV)： 标准差与期望的比值$$CV=\frac{\sqrt{D(X)}}{E(X)}=\frac{\sigma (X)}{E(X)}$$变异系数是个无量纲的量，从而消除了量纲对波动的影响。

分位数和中位数(Quantile and median)

分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点
P { x ⩽ x α } = α P\{x⩽ x_α\}=α P{x⩽xα​}=α此时$x_{\alpha }$称为 $\alpha$ 分位点。常用的有中位数（即二分位数）、四分位数、百分位数等。

协方差与相关系数(Covariance and correlation coefficient)

协方差(covariance)：由方差性质(3)的意义，定义$$\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)=E[(X-E(X))(Y-E(Y))]$$为 $X,Y$ 的协方差。
协方差的基本性质：(其中 a , b 为常数)
(1) 若 $X,Y$ 相互独立，则 $\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)=0$
(2) $\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)=\mathrm{C}\mathrm{o}\mathrm{v}(Y,X)$
(3) $D(X)=E[(X-E(X){)}^2]=\mathrm{C}\mathrm{o}\mathrm{v}(X,X)$
(4) $\mathrm{C}\mathrm{o}\mathrm{v}(aX,bY)=ab\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)$
(5) $\mathrm{C}\mathrm{o}\mathrm{v}(X_1+X_2,Y)=\mathrm{C}\mathrm{o}\mathrm{v}(X_1,Y)+\mathrm{C}\mathrm{o}\mathrm{v}(X_2,Y)$
(6) $D(X+Y)=D(X)+D(Y)+2\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)$
(7) $\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)=E(XY)-E(X)E(Y)$

相关系数(correlation coefficient)：协方差反映了随机变量X与Y的相关性（这种关系是什么关系？）。但协方差是有量纲的数字特征，为了消除其量纲的影响，考虑单位化的随机变量，令$$X^{\ast }=\frac{X-E(X)}{\sqrt{D(X)}},Y^{\ast }=\frac{Y-E(Y)}{\sqrt{D(Y)}}$$
引入一个新概念 $${\rho }_{XY}=\mathrm{C}\mathrm{o}\mathrm{v}(X^{\ast },Y^{\ast })=\frac{\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$$称为$X,Y$的相关系数

进一步考虑 $X,Y$之间的关系，考虑 $X,Y$之间的线性关系， 即 $\hat{Y}=a+bX$(a,b为常数) 近似的表示 $Y$，均方误差$e=E[(Y-\hat{Y}{)}^2]=E[(Y-(a+bX){)}^2]$
求 min ⁡ { e } \min\{e\} min{e}，令 $\frac{\partial e}{\partial a}=0,\frac{\partial e}{\partial b}=0$，解得 $b_0=\frac{\mathrm{C}\mathrm{o}\mathrm{v}(X,Y)}{D(X)},a_0=E(Y)-b_{0}E(X)$
带入可得 min ⁡ { e } = D ( Y ) ( 1 − ρ X Y 2 ) \min\{e\}=D(Y)(1-ρ^2_{XY}) min{e}=D(Y)(1−ρXY2​)

相关系数的性质：
(1) ${\rho }_{XY}⩽1$
(2) ${\rho }_{XY}=1⟺\exists a,b\in \mathbb{R},Y=aX+b$

相关系数的实际意义
相关系数是一个用来表征两个随机变量之间线性关系密切程度的特征数，有时也称为“线性相关系数”。
当${\rho }_{XY}$较大时，表明X与Y的线性关系程度较好；
当${\rho }_{XY}$较小时，表明X与Y的线性关系程度较差。
特别地，
当$|{\rho }_{XY}|=1$时，表明X与Y之间以概率1存在线性关系；
当${\rho }_{XY}=0$时，表明X与Y之间没有线性关系，称两个变量不相关。
X,Y相互独立$⟹$ X,Y不相关；但X,Y不相关不能判断X,Y相互独立

矩 (Moment)

参考链接：https://www.zhihu.com/question/23236070/answer/143316942

物理意义：数学中矩的概念来自物理学。在物理学中，矩是表示距离和物理量乘积的物理量，表征物体的空间分布。由其定义，矩通常需要一个参考点（基点或参考系）来定义距离。如力和参考点距离乘积得到的力矩（或扭矩），原则上任何物理量和距离相乘都会产生力矩，质量，电荷分布等。
如对空间密度积分${\nu }_k=\int r^k\rho (r)\mathrm{d}r$，如果点表示质量，则第零矩是总质量，一阶矩是重心，二阶矩是转动惯量。

数学意义：矩是物体形状识别的重要参数指标。在统计学中，矩是对变量分布和形态特点的一组度量。定义在实数域的实函数相对于值c的k阶矩为：$${\nu }_k={\int }_{-\infty }^{+\infty }(x-c{)}^{k}f(x)\mathrm{d}x$$如果点表示概率密度，则第零阶矩表示总概率（=1）。

(1) k阶(原点)矩(origin moment)：随机变量$X$的k阶(原点)矩定义为$${\mu }_k=E(X^k)$$

连续型：${\mu }_k={\int }_{-\infty }^{+\infty }{x}^{k}f(x)\mathrm{d}x={\int }_{-\infty }^{+\infty }{x}^k\mathrm{d}F(x)$，其中$f(x)$为概率密度函数。
离散型：${\mu }_k=\sum _{i=1}^{\infty }{x}_i^k{p}_i$，其中 P { X = x i } = p i P\{X=x_i\}=p_i P{X=xi​}=pi​为概率分布函数。
(2) k 阶中心矩(central moment)：移除均值后计算的矩被称为中心矩。 对于二阶及更高阶的矩，通常使用中心矩（围绕平均值的矩，均值是一阶矩），而不是原点矩，因为中心矩能更清楚的体现关于分布形状的信息。$${\nu }_k=E[(X-E(X){)}^k]$$

连续型：${\nu }_k={\int }_{-\infty }^{+\infty }[x-E(X){]}^{k}f(x)\mathrm{d}x$，其中$f(x)$为概率密度函数。
离散型：${\nu }_k=\sum _{i=1}^{\infty }[x_i-E(X){]}^k{p}_i$，其中 P { X = x i } = p i P\{X=x_i\}=p_i P{X=xi​}=pi​为概率分布函数。
期望和方差：随机变量的数学期望（expectation）即为其一阶原点矩 $E(X)$
方差（variance）即为二阶中心矩 $Var(X)=E[x-E(X){]}^2$

(3) $(k+l)$ 阶混合矩(mixed moment)：二维随机变量$(X,Y)$的$(k+l)$ 阶混合（原点）矩为$${\mu }_{kl}^{\prime }=E(X^k{Y}^l)$$

连续型：${\mu }_{kl}^{\prime }={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{x}^k{y}^{l}f(x,y)\mathrm{d}x\mathrm{d}y$，其中$f(x,y)$为概率密度函数。
离散型：${\mu }_{kl}^{\prime }=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{x}_i^k{y}_j^l{p}_{ij}$，其中 P { X = x i , Y = y j } = p i j P\{X=x_i,Y=y_j\}=p_{ij} P{X=xi​,Y=yj​}=pij​为概率分布函数。
(4) $(k+l)$ 阶混合中心距(mixed central moment)：随机变量$(X,Y)的(k+l)$ 阶中心矩被定义为$${\mu }_{kl}^{\prime }=E[(X-E(X){)}^k(Y-E(Y){)}^l]$$

连续型：${\mu }_{kl}^{\prime }={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }[x-E(X){]}^k[y-E(Y){]}^{l}f(x,y)\mathrm{d}x\mathrm{d}y$，其中$f(x,y)$为概率密度函数。
离散型：${\mu }_{kl}^{\prime }=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }[x_i-E(X){]}^k[y_j-E(Y){]}^l{p}_{ij}$，其中 P { X = x i , Y = y j } = p i j P\{X=x_i,Y=y_j\}=p_{ij} P{X=xi​,Y=yj​}=pij​为概率分布函数。

(1+1) 阶混合中心矩即为协方差。

矩母函数(moment generating function, MFG)：在统计学中，矩母函数是一个关于随机变量的实值函数，它可以替代密度函数来描述分布。也就是说，出了概率密度函数外，我们也可以通过矩母函数来描述分布。对于某些概率密度函数和累计密度函数比较复杂的情况，我们使用矩母函数分析分布会大大降低复杂性，尤其是对于随机变量的加权求和来说，矩母函数可以提供非常简单的计算。当然，矩母函数出了是基于实值函数，也可以是基于向量和矩阵的，扩展性很好。但是，并不是所有的分布都存在矩母函数。

定义随机变量 $e^{tX}$的数学期望为随机变量$X$的矩母函数：$$M_X(t)=E(e^{tX}),t\in \mathbb{R}$$

连续型：$M_X(t)={\int }_{-\infty }^{+\infty }\exp (tx)f(x)\mathrm{d}x$，其中$f(x)$为概率密度函数。
离散型：$M_X(t)=\sum \exp (t{x}_i)p_i$，其中 P { X = x i } = p i P\{X=x_i\}=p_i P{X=xi​}=pi​为概率分布函数。
另外，矩母函数的对数为累积量生成函数$R_X(t)=\ln M_X(t)$
矩母函数的性质
(1) 随机变量的矩母函数与概率分布具有一一对应关系，即
$M_Y(t)=M_X(t)⟺F_X(x)=F_Y(y)$
(2) 若随机变量$X_1,X_2,\cdots ,X_n$相互独立，则$Y=X_1+X_2+\cdots ,X_n$的矩母函数
$M_Y(t)=M_{X_1}(t)M_{X_1}(t)\cdots M_{X_1}(t)$
(3) 若 $Y=a+bX$，则矩母函数 $M_Y(t)=e^{at}{M}_X(bt)$

矩母函数的特征：以连续随机变量为例，离散型随机变量可做相同变换。
(1) 由泰勒级数 $e^x=1+x+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}+\cdots$，得
$M_X(t)=E(e^{tX})={\int }_{-\infty }^{+\infty }[1+tx+\frac{(tx{)}^2}{2!}+\cdots +\frac{(tx{)}^n}{n!}+\cdots ]f(x)\mathrm{d}x$，即$$M_X(t)=1+t{M}_1+\frac{t^2}{2!}{M}_2+\cdots +\frac{t^n}{n!}{M}_n+\cdots$$其中$M_i$为随机变量$X$的 $i$ 阶中心矩
(2) $M_X(-t)$ 是双侧拉普拉斯变换(Laplace Transform)
(3) 不管概率分布是不是连续，矩母函数都可以用黎曼-斯蒂尔切斯积分给出：$$M_X(t)={\int }_{-\infty }^{+\infty }{e}^{tx}\mathrm{d}F(x)$$其中，$F(x)$是累积分布函数(Cumulative Distribution Function, CDF)。

特征函数(characteristic function)：定义复随机变量 $e^{itX}$的数学期望为随机变量$X$的特征函数：$${\phi }_X(t)=E(e^{itX}),t\in \mathbb{R}$$特征函数与矩母函数的关系${\phi }_X(t)=M_X(it)$，由此可知特征函数与矩母函数有相同的性质

求随机变量的矩：如果随机变量$X$矩母函数存在，则各阶矩存在且可由矩量母函数表示$$E(X^k)=M_X^{(k)}(0)=\frac{{\mathrm{d}}^k{M}_X}{\mathrm{d}{t}^k}{|}_{t=0}$$特别的有$E(X)=M_X^{\prime }(0),Var(X)=M_X^{\prime \prime }(0)-[M_X^{\prime }(0){]}^2$

偏度和峰度(Skewness and kurtosis)

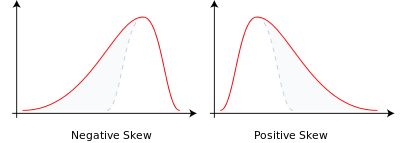
偏度(skewness)：随机变量的偏度（衡量分布不对称性）定义为
$S(X)=\frac{{\nu }_3}{{\nu }_2^{3/2}}=\frac{E[X-E(X){]}^3}{[Var(x){]}^{3/2}}$
任何对称分布偏态为0
$S<0$，向左偏斜（分布尾部在左侧较长，失效率数据常向左偏斜，如极少量的灯泡会立即烧坏）
$S>0$，向右偏斜分布（分布尾部在右侧较长，工资数据往往以这种方式偏斜，大多数人所得工资较少）
偏度无量纲，是描述分布偏离对称程度的一个特征数。

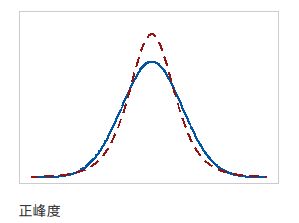
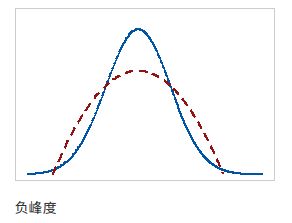
峰度(kurtosis)：一般随机变量的峰度定义为其四阶中心矩与方差平方的比值再减3，减3是为了让正态分布峰度为0，这也被称为超值峰度。
$K(X)=\frac{{\nu }_4}{{\nu }_2^2}-3=\frac{E[x-E(X){]}^4}{Va{r}^2(X)}-3$
完全符合正态分布的数据峰度值为0，且正态分布曲线被称为基线。峰度无量纲，是相对于正态分布而言的超出量。
$K>0$，标准化后的分布比标准正态分布剑鞘
$K<0$，标准化后的分布比标准正态分布平坦

协方差矩阵与多维正态分布(Covariance matrix and multivariate normal distribution)

协方差矩阵(Covariance matrix)：设n维随机变量$\mathbf{X}=(X_1,X_2,\cdots ,X_n)$，记$c_{ij}=\mathrm{C}\mathrm{o}\mathrm{v}(X_i,X_j)(i,j=1,2,\cdots ,n)$，则称$C=(c_{i}j{)}_{n\times n}$为随机向量 $\mathbf{X}$ 的协方差矩阵。
协方差矩阵的性质：
(1) $C=C^T$, 即协方差阵为对称阵
(2) $C⩾0$ , 即协方差阵为非负定矩阵
定理 ：设 $(X,Y)\sim N({\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2,\rho )$，则
(1) $X,Y$的相关系数 ${\rho }_{XY}=\rho$
(2) $X,Y$的协方差矩阵为$C=\left(\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2\end{array}\right)$
(3) $X,Y$相互独立
$⟺{\rho }_{XY}=\rho =0$
$⟺X,Y$互不相关
二维正态随机变量密度函数的矩阵表示法
f ( x ) = 1 2 π ∣ C ∣ 1 / 2 exp ⁡ { − 1 2 ( x − μ ) C − 1 ( x − μ ) T } f(\mathbf{x})=\dfrac{1}{2π|C|^{1/2}}\exp\{-\dfrac{1}{2}(\mathbf{x-μ})C^{-1}(\mathbf{x-μ})^T\} f(x)=2π∣C∣1/21​exp{−21​(x−μ)C−1(x−μ)T}
其中 $\mathbf{x}=(x,y),\mu =({\mu }_1,{\mu }_2),C$为协方差阵

n维正态随机变量：设 $C$ 为 n 阶正定对称阵，$\mu =({\mu }_1,{\mu }_2,\cdots ,{\mu }_n)$为n维已知向量，记 $\mathbf{x}=(x_1,x_2,\cdots ,x_n)\in {\mathbb{R}}^n$，若n维正态随机向量$\mathbf{X}=(X_1,X_2,\cdots ,X_n)$的密度函数为
f ( x ) = 1 ( 2 π ) n / 2 ∣ C ∣ 1 / 2 exp ⁡ { − 1 2 ( x − μ ) C − 1 ( x − μ ) T } f(\mathbf{x})=\dfrac{1}{(2π)^{n/2}|C|^{1/2}}\exp\{-\dfrac{1}{2}(\mathbf{x-μ})C^{-1}(\mathbf{x-μ})^T\} f(x)=(2π)n/2∣C∣1/21​exp{−21​(x−μ)C−1(x−μ)T}
则称 $\mathbf{X}$ 服从 n 维正态分布, 记为 $\mathbf{X}=(X_1,X_2,\cdots ,X_n)\sim N(\mu ,C)$

n 维正态分布的性质：$\mathbf{X}=(X_1,X_2,\cdots ,X_n)\sim N(\mu ,C)$
(1) $f(\mathbf{x})>0$
(2) ${\int }_{-\infty }^{+\infty }\cdots {\int }_{-\infty }^{+\infty }f(x_1,x_2,\cdots ,x_n)\mathrm{d}{x}_1\mathrm{d}{x}_2\cdots \mathrm{d}{x}_n=1$
(3) ${\mu }_i=E(x_i)(1=1,2,\cdots ,n)$
(4) $C=(c_{ij}{)}_{n\times n}$是$(X_1,X_2,\cdots ,X_n)$的协方差矩阵，且
$$\begin{gathered} D(X_i)=c_{ii}(1=1,2,\cdots ,n) \\ \mathrm{C}\mathrm{o}\mathrm{v}(X_i,X_j)=c_{ij}(1=1,2,\cdots ,n) \end{gathered}$$
(5) $X_i\sim N({\mu }_i,c_{ii})(1=1,2,\cdots ,n)$
(6) 若 $X_1,X_2,\cdots ,X_n$相互独立，且各$X_i\sim N({\mu }_i,{\sigma }_i^2)$，则
$(X_1,X_2,\cdots ,X_n)\sim N(\mu ,C)$，其中$\mu =({\mu }_1,{\mu }_2,\cdots ,{\mu }_n),C=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\sigma }_1^2,{\sigma }_1^2\cdots ,{\sigma }_n^2)$

重要定理 $\mathbf{X}=(X_1,X_2,\cdots ,X_n)\sim N(\mu ,C)$
(1) 其任意 $k(1⩽k⩽n)$维子向量均服从k维正态分布
(2) $\mathbf{X}=(X_1,X_2,\cdots ,X_n)\sim N(\mu ,C)⟺X_1,X_2,\cdots ,X_n$的任一非零线性组合$l_1{X}_1+l_2{X}_2+\cdots l_n{X}_n$服从一维正态分布
(3) 正态随机向量的线性变换不变性： 令$Y=XA$，其中$A=(a_{ij}{)}_{n\times m}$，则$Y=(Y_1,Y_2,\cdots ,Y_m)$ 仍服从多维正态分布
(4) $X_1,X_2,\cdots ,X_n$相互独立
$⟺X_1,X_2,\cdots ,X_n$两两不相关
$⟺C=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(c_{11},c_{22},\cdots ,c_{nn})$(即C为对角阵)

大数定律和中心极限定理(Law of Large Numbers & Central Limit Theorem)

依概率收敛 (convergence in probability)：回顾概率的概念是如何产生的?

设$n$次独立重复试验中事件$A$发生的次数为$n_A$则当$n$越来越大时，有
∀ ϵ > 0 , lim ⁡ n → ∞ P { ∣ n A n − p ∣ ⩾ ϵ } = 0 ∀ ϵ>0,\lim\limits_{n\to∞}P\{|\dfrac{n_A}{n}-p|⩾ ϵ\}=0 ∀ϵ>0,n→∞lim​P{∣nnA​​−p∣⩾ϵ}=0这种收敛性称为依概率收敛。

定义：设 $Y_1,Y_2,\cdots ,Y_n,\cdots$为一随机变量序列，c为一常数，若对于$\forall ϵ>0$均有 lim ⁡ n → ∞ P { ∣ Y n − c ∣ ⩾ ϵ } = 0 \lim\limits_{n\to∞}P\{|Y_n-c|⩾ ϵ\}=0 n→∞lim​P{∣Yn​−c∣⩾ϵ}=0成立，则称随机变量序列依概率收敛于c，记为 $$Y_n\stackrel{P}{\to }c(n\to \infty )$$

性质：若 $X_n\stackrel{P}{\to }a,Y_n\stackrel{P}{\to }b(n\to \infty )$，函$g(x,y)$在点$(a,b)$处连续，那么
$g(X_n,Y_n)\stackrel{P}{\to }g(a,b)(n\to \infty )$
特别的，若 $X_n\stackrel{P}{\to }a(n\to \infty )$，函数$f(x)$在点$a$处连续，那么$f(X_n)\stackrel{P}{\to }f(a)(n\to \infty )$

大数定律(Law of Large Numbers)

Bernoulli 大数定律 设 $n_A$ 是 $n$ 次独立重复试验中事件 $A$ 发生的次数，且 $P(A)=p$，则对于$\forall ϵ>0$有
lim ⁡ n → ∞ P { ∣ n A n − p ∣ ⩾ ϵ } = 0 \lim\limits_{n\to∞}P\{|\dfrac{n_A}{n}-p|⩾ ϵ\}=0 n→∞lim​P{∣nnA​​−p∣⩾ϵ}=0，即$\frac{n_A}{n}\stackrel{P}{\to }p(n\to \infty )$ 频率稳定于概率

Chebyshev 大数定律 设 $X_1,X_2,\cdots ,X_n,\cdots$为相互独立的随机变量序列，且具有相同的数学期望 $\mu$ 和方差${\sigma }^2$，则对于$\forall ϵ>0$有
lim ⁡ n → ∞ P { ∣ 1 n ∑ i = 1 n X i − μ ∣ ⩾ ϵ } = 0 \lim\limits_{n\to∞}P\{|\dfrac{1}{n}\displaystyle\sum_{i=1}^{n}X_i-μ|⩾ ϵ\}=0 n→∞lim​P{∣n1​i=1∑n​Xi​−μ∣⩾ϵ}=0，即$\frac{1}{n}\sum _{i=1}^n{X}_i\stackrel{P}{\to }\mu (n\to \infty )$ 平均值稳定于期望

Sinchin 大数定律 设 $X_1,X_2,\cdots ,X_n,\cdots$为独立同分布(independent identically distri- buted;IID)的随机变量序列，且其期望为 $\mu$ 和方差${\sigma }^2$，则对于$\forall ϵ>0$有
lim ⁡ n → ∞ P { ∣ 1 n ∑ i = 1 n X i − μ ∣ ⩾ ϵ } = 0 \lim\limits_{n\to∞}P\{|\dfrac{1}{n}\displaystyle\sum_{i=1}^{n}X_i-μ|⩾ ϵ\}=0 n→∞lim​P{∣n1​i=1∑n​Xi​−μ∣⩾ϵ}=0，即$\frac{1}{n}\sum _{i=1}^n{X}_i\stackrel{P}{\to }\mu (n\to \infty )$

大数定律的意义
(1) 给出了“频率稳定性”的严格数学解释.
(2) 提供了通过试验来确定事件概率的方法.
(3) 是数理统计中参数估计的重要理论依据之一.
(4) 是Monte Carlo方法¹的主要数学理论基础.

中心极限定理(Central Limit Theorem)

有许多随机变量，它们是由大量的相互独立的随机变量的综合影响所形成的，而其中每个个别的因素作用都很小，这种随机变量往往服从或近似服从正态分布，或者说它的极限分布是正态分布，中心极限定理正是从数学上论证了这一现象，它在长达两个世纪的时期内曾是概率论研究的中心课题。

独立同分布的中心极限定理设 $X_1,X_2,\cdots ,X_n,\cdots$为独立同分布的随机变量序列，且其期望为 $\mu$ 和方差${\sigma }^2$，则随机变量之和 $Y_n=\sum _{i=1}^n{X}_i$ 的标准化变量$$Z_n=\frac{Y_n-E(Y_n)}{\sqrt{D(Y_n)}}=\frac{\sum _{i=1}^n{X}_i-n\mu }{\sqrt{n}\sigma }$$的分布函数$F_n(x)$对于 $\forall x\in \mathbb{R}$，有$$\begin{array}{rl}\underset{n\to \infty }{\lim }{F}_n(x)& =\underset{n\to \infty }{\lim }P\left\{\frac{\sum _{i=1}^n{X}_i-n\mu }{\sqrt{n}\sigma }⩽x\right\}\\ & ={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }}{e}^{-t^2/2}\mathrm{d}t=\Phi (x)\end{array}$$
故可认为$\underset{n\to \infty }{\lim }\sum _{i=1}^n{X}_i\sim N(n\mu ,n{\sigma }^2)$，上式可改成当 $\underset{n\to \infty }{\lim }\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$或$\underset{n\to \infty }{\lim }\bar{X}\sim N(\mu ,{\sigma }^2/n)$

李雅普诺夫(Lyapunov)中心极限定理设 随机变量$X_1,X_2,\cdots ,X_n,\cdots$相互独立，他们具有数学期望 $E(X_k)={\mu }_k$ 和方差$D(X_k)={\sigma }_k^2$
记$B_n^2=\sum _{k=1}^n{\sigma }_k^2$，若$\exists \delta >0,\frac{1}{B_n^{2+\delta }}\sum _{k=1}^{n}E(|X_k-{\mu }_k{|}^{2+\delta })\to 0(n\to \infty )$
则随机变量之和 $Y_n=\sum _{k=1}^n{X}_k$ 的标准化变量$$Z_n=\frac{Y_n-E(Y_n)}{\sqrt{D(Y_n)}}=\frac{\sum _{k=1}^n{X}_k-\sum _{k=1}^n{\mu }_k}{B_n}$$的分布函数$F_n(x)$对于 $\forall x\in \mathbb{R}$，有$$\begin{array}{rl}\underset{n\to \infty }{\lim }{F}_n(x)& =\underset{n\to \infty }{\lim }P\left\{\frac{\sum _{k=1}^n{X}_k-\sum _{k=1}^n{\mu }_k}{B_n}⩽x\right\}\\ & ={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }}{e}^{-t^2/2}\mathrm{d}t=\Phi (x)\end{array}$$
故可认为 $\underset{n\to \infty }{\lim }\sum _{k=1}^n{X}_k\sim N(\sum _{k=1}^n{\mu }_k,B_n^2)$

棣莫弗-拉普拉斯(De Moivre-Laplace)中心极限定理：若随机变量序列 ${\eta }_n\sim B(n,p)(n=1,2,\cdots )$，则对于 $\forall x\in \mathbb{R}$，有$$\begin{gathered} \underset{n\to \infty }{\lim }P\left\{\frac{{\eta }_n-np}{\sqrt{np(1-p)}}⩽x\right\} \\ ={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }}{e}^{-t^2/2}\mathrm{d}t=\Phi (x) \end{gathered}$$
故可认为 $\underset{n\to \infty }{\lim }{\eta }_n\sim N(np,np(1-p))$，这个定理是CLT定理的一种特殊情况，说明了正态分布是二项分布的极限分布。

中心极限定理的意义：在实际问题中，如果某随机指标满足
(1) 该指标是由大量相互独立的随机因素迭加而成
(2) 每个因素作用都是微小的，且没有一个因素起到突出的作用
则这个随机指标近似地服从正态分布。

在实际问题中，所考虑的随机变量可以表示成多个独立的随机变量之和，如在任意指定时刻，一城市的耗电量是大量用户耗电量的总和；一个物理实验的测量误差是由许多观察不到的、可叠加的微小误差所合成的；它们往往近似服从正态分布。

附录

常见的离散型随机变量

分布	概率分布	累积分布函数	期望	方差	矩母函数
伯努利分布 $B(1,p)$	$p(1-p)$		$p$	$p(1-p)$	$1-p+p{e}^t$
二项分布 $B(n,p)$	${\complement }_n^k{p}^k(1-p{)}^{n-k}$ $(k=1,2,\cdots ,n)$	$\sum _{i=1}^k{\complement }_n^i{p}^i(1-p{)}^{n-i}$	$np$	$np(1-p)$	$(1-p+p{e}^t{)}^n$
几何分布 $Geom(p)$	$p(1-p{)}^{k-1}$ $(k\in \mathbb{N})$	$1-(1-p{)}^k$	$\frac{1}{p}$	$\frac{1-p}{p^2}$	$\frac{p{e}^t}{1-(1-p)e^t}$
泊松分布 $P(\lambda )$	$\frac{{\lambda }^k{e}^{-\lambda }}{k!}$ $(k\in \mathbb{N})$	$e^{-\lambda }\sum _{i=1}^k\frac{{\lambda }^i}{i!}$	$\lambda$	$\lambda$	$\exp (\lambda (e^t-1))$

常见的连续型随机变量

分布	概率密度	累积分布函数	期望	方差	矩母函数
均匀分布 $U(a,b)$	$\frac{1}{b-a}$ $(x\in [a,b])$	$\frac{x-a}{b-a}$	$\frac{a+b}{2}$	$\frac{(b-a{)}^2}{12}$	$\frac{e^{bt}-e^{at}}{t(b-a)}$
指数分布 $Exp(\theta )$	$\frac{1}{\theta }{e}^{-x/\theta }$ $(x>0)$	$1-e^{-x/\theta }$	$\theta$	${\theta }^2$	$\frac{1}{1-\theta t}$
正态分布 $N(\mu ,{\sigma }^2)$	$\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$ $(\mu \in \mathbb{R},\sigma >0)$		$\mu$	${\sigma }^2$	$\exp (\mu t+\frac{1}{2}{\sigma }^2{t}^2)$
伽马分布 $Gamma(k,\theta )$	$\frac{{\theta }^k}{\Gamma (k)}{x}^{k-1}{e}^{-\theta x}$ $(x>0)$ $\Gamma (k)={\int }_0^{\infty }{x}^{k-1}{e}^{-x}\mathrm{d}x$		$k\theta$	$k{\theta }^2$	$(1-\theta t{)}^{-k}$ $(t<1/\theta )$

---

1. Monte Carlo方法或称为计算机随机模拟方法、计算机仿真方法,是科学与工程中的一种重要工具。Monte Carlo 方法的原理主要基于大数定律. ↩︎