离散数学基础版1.0

最新推荐文章于 2023-08-25 03:58:38 发布

Seirohappy

最新推荐文章于 2023-08-25 03:58:38 发布

阅读量840

点赞数

分类专栏：机器学习数学语言

本文链接：https://blog.csdn.net/qq_41554955/article/details/116395275

版权

机器学习数学语言专栏收录该内容

4 篇文章 0 订阅

订阅专栏

离散数学基础版1.0

1.集合

1.1集合的定义：

集合的定义有三种：列举法，谓词法，韦恩图法.
“列举法"形如：A={0,1,2,3}
"谓词法"形如：A={ x $\in$ N|x mod 2=1}
"韦恩图法"形如：在这里插入图片描述

1.1.2集合的用途：

描述对象，每个对象对应的属性不一样，用不同的集合表示不同的对象，在机器学习中用来做标签。

答：(1).4个元素，分别是0，1，{0，1}，{1，2}，
（2).优点：一个集合可以储存不同类型的元素（单个字符，一个集合），可以表示一个多属性的对象。
（3）.若在程序中使用元组，要增删改的消耗大，所以对于集合的元组元组无法进行写操作，因此不支持append、extend、insert等操作，集合中的每个元组可以读，元组的读取操作（与列表一致，使用索引）

2基数：

2.1基数的定义:

基数表示集合的大小，例如一个集合A的基数表示为|A|,读作cadinalty of A.
在这里插入图片描述

（1）.0；空集里面没有元素。
（2）.1;该集合有一个元素，该元素是一个空集。

3.笛卡尔积

3.1笛卡尔积的定义:

两个集合X和Y的笛卡尔积，表示为X $\times$ Y，第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员。

3.2笛卡尔积的表示：

（1）.矩阵法：

3.3笛卡尔积的有序性，所以不支持结合律：

有些地方为了说明元素的有序性，笛卡尔积是有序性的，使用<x,y>而不是（x,y）;对于表示向量时，表示向量是 $\left |x_{1},...,x_{n} \right |$ ，而不是 $\left (x _{1},...,x_{n} \right )$ 。
笛卡尔积不支持结合律，所以不一定满足(A x B) x C=A x (B x C)
若A = { a }，B={b}，C={c}:
(1). $A\times B=\left \{ \left ( a,b \right ) \right \}$ ;
(2). $\left ( A\times B \right ) \times C=\left \{ \left ( a,b \right ) ,c \right \}$ ;
(3). $A\times \left ( B\times C \right ) =\left \{ a,\left ( b,c \right ) \right \}$ ;

3.4笛卡尔积对并运算和交运算满足分配律。

4. 数据集

4.1什么是数据集：

若C是基数为3的集合，S为基数为4的集合，W为基数为5的集合，则则几个集合的笛卡尔积后的新集合R的基数为 $3\times4\times 5=60$ （C,S,W的笛卡尔积元素个数为60）,数据集是笛卡尔集中的任意个元素，其大小小于等于笛卡尔积元素个数。

4.2数据集的表示：

在这里插入图片描述

4.3列向量表示一个对象

在机器学习中，通常用一个列向量表示一个对象，这种情况下, 矩阵表示法中应使用 $D=\left \{x_{0},x_{1}...,x_{n} \right \}$ 即不用使用转置符号。

5.幂集

5.1幂集的概念：

若A为为任意集合，以A的子集为元素所组成的集合，称为A的幂集，例如A={1，2，3},则A的幂集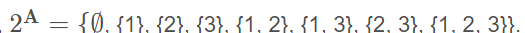，在这里插入图片描述

6.二元关系

二元关系来描述两个值的关系，例如大小关系是一种二元关系，若第一个值设为X，另一个是Y，（1）当X=Y时，表示的就是二维直角坐标系的表示过45度这条直线，（2）当X<Y时，就是二维直角坐标系中表示过45度这条直线的左上，（3）X>Y时，就是二维直角坐标系中表示过45度这条直线的右下。

6.1关系的拓展：

三元关系，四元关系，…,n元关系，多少“元”表示的有多少个变量，描述的是，这些变量的关系。
例如:一个三元关系: $\left \{ \left ( x,y,z \right ) ,x^{2}+y^{2}+z^{2}=1\right \}$

7.函数

函数是为了讨论输入到输出的映射，数学中我们接触到很多函数模型，这里不必多说。
在这里插入图片描述

算，学习器讨论的也是输入到输出的映射，我们通过输入数据，通过关系的映射求得输出数据。

8.元组

8.1元组=对象的类

元组的各个部分，即可以是一个集合，也可以是一个基本元素。
在这里插入图片描述

可以完整的表达，因为“元组=类”，在程序设计中，元组应封装成一个类，不仅能表示实例对象的数据，也能覆盖任何操作。
代码如下：
#include <iostream>
#include <vector>
#include <tuple>
using namespace std;

//描述一个人
void getDescription(string name,int age){
    cout<<name<<"的年龄是:"<<age<<endl;
}

int main()
{
  //一个元组表示一个人
    tuple<string,int,void(*)(string,int)> person("Amy",10,getDescription);
    
 //得到这个元组的数据，操作这个元组的方法
    get<2>(person)(get<0>(person),get<1>(person));

    return 0;
}

打印结果：
在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/2021050411035099.png
Definition 7:A binary tree is a tuple $T_{b}=(V,r,c)$ ,where $V=\left \{ v_{1}...v_{n} \right \}$ is the value of the node，r is root，c: $V\cup \left \{\phi \right \} \times \sum {^{*}} \longrightarrow V\cup \left \{ \phi \right \}$ satisfying.
在这里插入图片描述
Definition 8 :An undirected weighted graph is a tuple $G_{w}=(V,w)$ ,w : $\times V->\mathbb{R}^{+} \cup \left \{ 0\right \}$ is the edge weight function,and $w(v_{i},v_{j})=w(v_{j},v_{i})$ .

Definition 9:Let $\sum=\left \{ {l,r} \right \}$ be the alphbet and $\phi$ be a null node. A binary tree is a triple T = ( V , r , c ) , where $V=\left \{ v_{1}...v_{n} \right \}$ is the set of nodes, ${\in}V$ is the root,and we say there is a relationship c,c: $V\cup \left \{\phi \right \} \times \sum {^{*}} \longrightarrow V\cup \left \{ \phi \right \}$ satisfying.
(a). $\forall v\in V,\exists 1 s\in\sum {^{*}} st.c(r,s)=v$
在这里插入图片描述

在这里插入图片描述
Definition 10:A deterministic finite state automata binary tree is a tuple $T_{b}=(\sum,V,q_{0},T,f)$ ,where $\sum$ is {l,r}, $V=\left \{ v_{1}...v_{n} \right \}$ , $q_{0}$ is the root of binary tree,T is the end node meaning is null,f is the transition function,f: $V\cup \left \{\phi \right \} \times \sum {^{*}} \longrightarrow V\cup \left \{ \phi \right \}$ satisfied .
(a). $\forall v\in V,\exists 1 s\in\sum {^{*}} st.f(r,s)=v$
在这里插入图片描述
Definition 11:The tree is a This is an n-tree,a node of tree can have up to n children.A deterministic finite state automata tree is a tuple $T=(\sum,V,q_{0},T,f)$ ，where $\sum$ ={0,1,…,n-1}, $V=\left \{ v_{1}...v_{n} \right \}$ , $q_{0}$ is the root of binary tree,T is the end node meaning is null,f is the transition function,f: $V\cup \left \{\phi \right \} \times \sum {^{*}} \longrightarrow V\cup \left \{ \phi \right \}$ satisfied .
(a). $\forall v\in V,\exists 1 s\in\sum {^{*}} st.c(v,s)=r$

Seirohappy

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
离散数学基础版1.0

离散数学基础版1.01.集合1.1集合的定义：集合的定义有三种：列举法，谓词法，韦恩图法.“列举法"形如：A={0,1,2,3}"谓词法"形如：A={ x∈N|x mod 2=1}"韦恩图法"形如：1.1.2集合的用途：描述对象，每个对象对应的属性不一样，用不同的集合表示不同的对象，在机器学习中用来做标签。答：(1).4个元素，分别是0，1，{0，1}，{1，2}，（2).优点：一个集合可以储存不同类型的元素（单个字符，一个集合），可以表示一个多属性的对象。（3）.若在程序中使用元组
复制链接

扫一扫