【数据结构】图—普里姆（Prim）算法（原理和C程序解释）

---

---

一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树（不存在回路）的n-1条边。将生成树的各边的权值相加，就是代价，我们将连通网的最小代价生成树称为最小生成树。

查找无向连通网的最小生成树，有两种经典算法—普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法，本文介绍普里姆算法。

理解本文需要先了解图的一些构造方法，参考【数据结构】图的创建与遍历

---

一、定义

普利姆算法定义如下：

假设$N=(V,E)$是连通网，$TE$是$N$上最小生成树中边的集合。算法从 U = { u 0 } ( u 0 ∈ V ) , T E = { } U = \{u_0\} \quad (u_0 \in V), \quad TE = \{\} U={ u0​}(u0​∈V),TE={ }开始。重复执行以下操作：在所有$u\in U,v\in V-U$的边$(u,v)\in E$中找到一条代价最小的边$(u_0,v_0)$并入集合$TE$，同时$v_0$并入$U$，直至$U=V$为止。此时$TE$中必有$n-1$条边，则$T=(V,TE)$为$N$的最小生成树。

---

二、实现思路

下图是一个连通网，我们以此来介绍普利姆算法的实现过程。

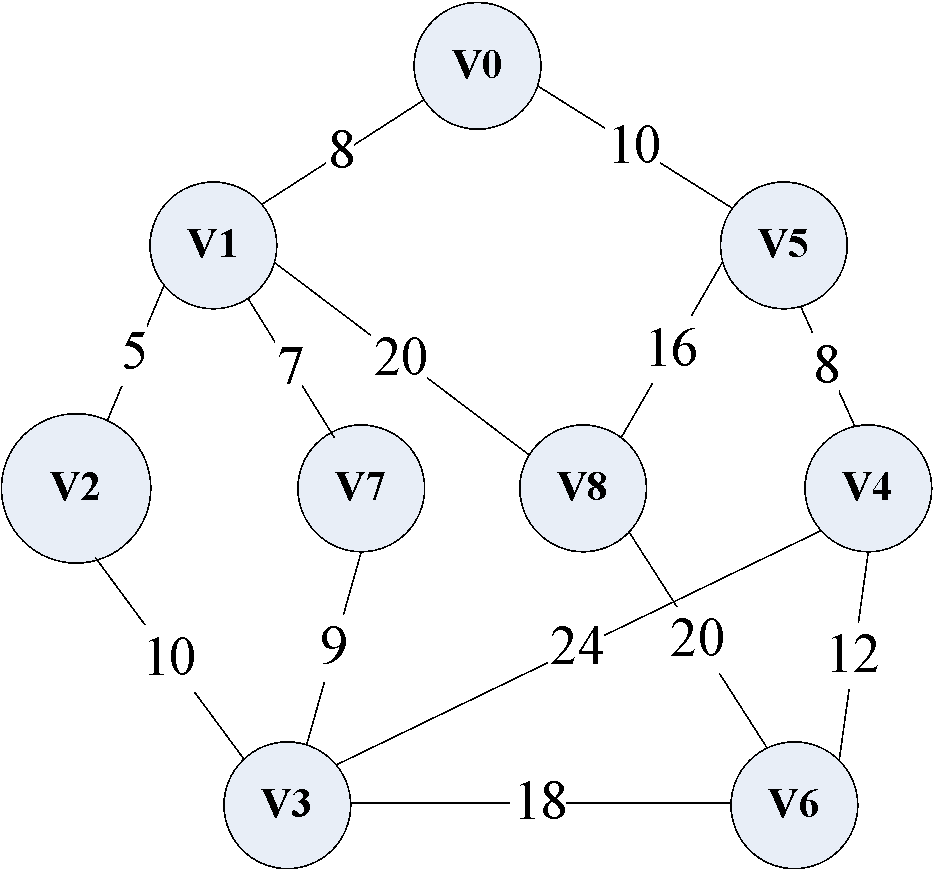
此连通网$N=(V,E)$，V是所有顶点的集合，E是所有边的集合。

U = { v 0 } ( v 0 ∈ V ) U = \{v_0\} \quad (v_0 \in V) U={ v0​}(v0​∈V)，$U$是生成树的点集合，以$v_0$为起点，开始寻找最短路径。

T E = { } TE = \{\} TE={ }是生成树的边集合，初始为空。

---

每次寻找离生成树最近的顶点，将其纳入生成树中，直至包含所有顶点：

（1）

U = { v 0 , v 1 } U = \{v_0, v_1\} U={ v0​,v1​}， T E = { ( v 0 , v 1 ) } TE = \{(v_0,v_1)\} TE={ (v0​,v1​)}。

（2）

U = { v 0 , v 1 , v 2 } U = \{v_0, v_1, v_2\} U={ v