图像特征的分类:边缘、角点、纹理。
角点检测(准确来说角点不是特征,但检测出来的角点可以用来提取和表示总结为特征)也被称为特征点检测,Harris是基于角点的特征描述子,主要用于图像特征点的匹配,属于图像的局部特征。
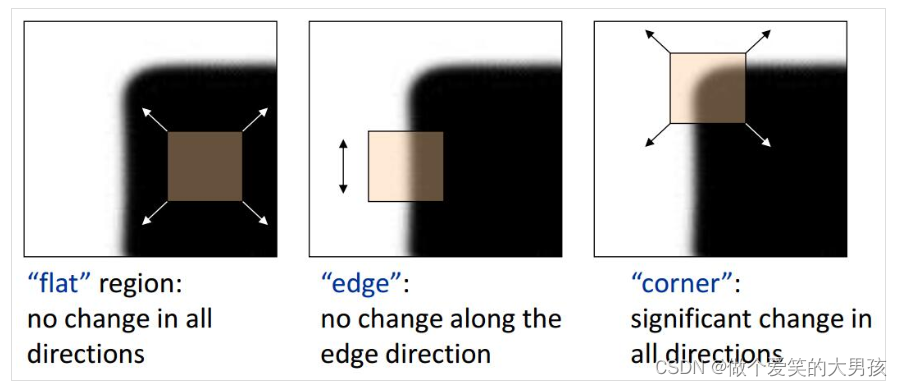
- 在局部小范围里,如果在各个方向上移动窗口,窗口区域内的灰度发生较大变化,就认为在窗口内遇到了角点,如下图右边第三幅图所示。
- 在局部小范围里,如果窗口在某个方向移动时,窗口内图像的灰度发生了较大的变化,而在另一些方向上没有发生变化,那么就认为窗口内的图像可能就是边缘区域,如下图第二幅图所示。
下面我们描述下Harris角点检测的原理。
对于局部区域来说,局部窗可以向四周移动。我们假设当前窗内的每个像素坐标为 ( x i , y j ) \left(x_i,y_j\right) (xi,yj),其中 ( x i , y j ) ∈ W \left(x_i,y_j\right)\in W (xi,yj)∈W,如果窗口为3x3大小,那么 i = 1 , 2 , 3 ; j = 1 , 2 , 3 i=1,2,3;j=1,2,3 i=1,2,3;j=1,2,3。当我们令窗偏移 ( u , v ) \left(u,v\right) (u,v)像素时,则我们定义差分平方的加权求和(SSD)为: E ( u , v ) = ∑ ( x i , y j ) ∈ W ω ( x i , y j ) [ I ( x i + u , y j + v ) − I ( x i , y j ) ] 2 E(u,v)=\displaystyle\sum_{(x_i,y_j)\in W} \omega(x_i,y_j)[I(x_i+u,y_j+v)-I(x_i,y_j)]^2 E(u,v)=(xi,yj)∈W∑ω(xi,yj)[I(xi+u,yj+v)−I(xi,yj)]2
其中 ω ( x i , y j ) , i = 1 , 2 , 3 ; j = 1 , 2 , 3 \omega(x_i,y_j),i=1,2,3;j=1,2,3 ω(xi,yj),i=1,2,3;j=1,2,3表示每个像素的权重,常用的权重核为高斯核,也可以设置全都是1。
我们用图详细描述下上面的这个过程。
取7x7图像局部区域如下:
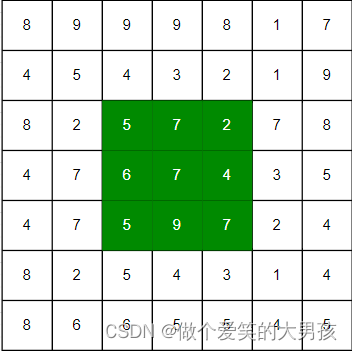
在其中我们又取一个3x3的窗口(用绿色标出)。
上面的
ω
(
x
i
,
y
j
)
,
i
=
1
,
2
,
3
;
j
=
1
,
2
,
3
\omega(x_i,y_j),i=1,2,3;j=1,2,3
ω(xi,yj),i=1,2,3;j=1,2,3可以理解为就是一个3x3的高斯核(RBF,径向基函数)。具体计算如下:
一维正态分布函数(也叫高斯函数),它的公式是:
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
/
2
σ
2
f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-(x-\mu)^2/2\sigma^2}
f(x)=σ2π1e−(x−μ)2/2σ2
其中,
μ
\mu
μ是x的均值,
σ
\sigma
σ是x的方差,在计算平均值时,中心点就是原点,所以
μ
=
0
\mu=0
μ=0。
根据一维高斯函数,可以推导得到二维高斯函数:
G
(
x
,
y
)
=
1
2
π
σ
2
e
−
(
x
2
+
y
2
)
/
2
σ
2
G(x,y)=\frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2}
G(x,y)=2πσ21e−(x2+y2)/2σ2
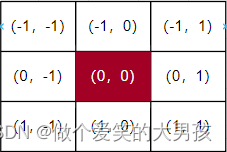
通过这个函数,我们就可以计算高斯核中每一个像素点位置的权重。假定中心点坐标是(0,0),那么距离它最近的8个点坐标如下:
然后通过上面的二维高斯函数计算权重矩阵,公式中x和y已知,
σ
\sigma
σ未知,所以需要设定
σ
\sigma
σ的值。这里假定
σ
=
1.5
\sigma=1.5
σ=1.5,则权重矩阵如下:
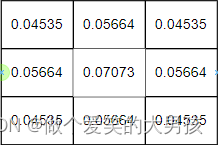
这九个点的权重和等于0.47871,我们要计算的是每个像素点的加权平均,所以必须让它们的权重之和等于1,因此上面9个值还要分别除以0.47871,得到最终的权重矩阵
ω
(
x
,
y
)
\omega(x,y)
ω(x,y)。
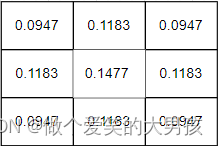
再次观察
E
(
u
,
v
)
E(u,v)
E(u,v)的公式,现在我们已经知道了
ω
(
x
i
,
y
i
)
\omega(x_i,y_i)
ω(xi,yi),这里我们假设
u
=
2
,
v
=
2
u=2,v=2
u=2,v=2,那么
[
I
(
x
i
+
u
,
y
j
+
v
)
−
I
(
x
i
,
y
j
)
]
2
[I(x_i+u,y_j+v)-I(x_i,y_j)]^2
[I(xi+u,yj+v)−I(xi,yj)]2在图像局部区域中如下红色部分表示:
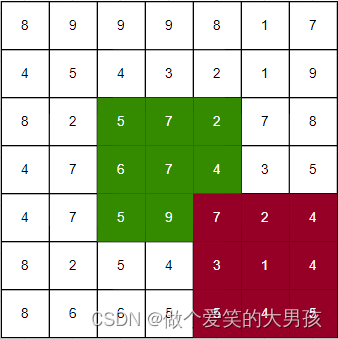
相当于将以前的窗口行和列都加2。
这时我们将
ω
\omega
ω中各点的权重和其红色区域中对应的像素点相乘然后相加就可以得到
E
(
2
,
2
)
E(2,2)
E(2,2)的值。
我们的目标:就是研究找像素点,该像素无论在哪个方向上,SSD都会有很大的值。
数学推导
对SSD公式进行泰勒展开,
o
(
I
)
o(I)
o(I)表示高阶小项:
I
(
x
+
u
,
y
+
v
)
=
I
(
x
,
y
)
+
∂
I
∂
x
u
+
∂
I
∂
y
v
+
o
(
I
)
I(x+u,y+v)=I(x,y)+\frac{\partial I}{\partial x}u+\frac{\partial I}{\partial y}v+o(I)
I(x+u,y+v)=I(x,y)+∂x∂Iu+∂y∂Iv+o(I)
去掉高阶小项,令
I
x
=
∂
I
∂
x
I_x=\frac{\partial I}{\partial x}
Ix=∂x∂I,
I
y
=
∂
I
∂
y
I_y=\frac{\partial I}{\partial y}
Iy=∂y∂I,表示像素在x方向和y方向的梯度。可以近似为:
I
(
x
+
u
,
y
+
v
)
≈
I
(
x
,
y
)
+
[
I
x
I
y
]
[
n
k
]
I(x+u,y+v)\approx I(x,y)+\lbrack I_x \quad I_y\rbrack{n\brack k}
I(x+u,y+v)≈I(x,y)+[IxIy][kn]
这时SSD近似等于:
E
(
u
,
v
)
≈
∑
(
x
,
y
)
∈
W
ω
(
x
,
y
)
[
[
I
x
I
y
]
[
n
k
]
]
2
E(u,v)\approx \displaystyle\sum_{(x,y)\in W}\omega(x,y)\lbrack \lbrack I_x \quad I_y\rbrack{n\brack k}\rbrack^2
E(u,v)≈(x,y)∈W∑ω(x,y)[[IxIy][kn]]2。
因为:
[
[
I
x
I
y
]
[
n
k
]
]
2
=
[
u
v
]
[
I
x
2
I
x
I
y
I
y
I
x
I
y
2
]
[
u
v
]
\lbrack \lbrack I_x \quad I_y\rbrack{n\brack k}\rbrack^2=\lbrack u\quad v\rbrack \begin{bmatrix} I_x^2 & I_xI_y \\ I_yI_x & I_y^2 \end{bmatrix}{u\brack v}
[[IxIy][kn]]2=[uv][Ix2IyIxIxIyIy2][vu]
我们发现
[
u
v
]
\lbrack u\quad v\rbrack
[uv]是可以单独拿出来到
∑
\displaystyle\sum
∑外面的,因此近似的SSD可以写为:
E
(
u
,
v
)
≈
[
u
v
]
(
∑
(
x
,
y
)
∈
W
ω
(
x
,
y
)
[
I
x
2
I
x
I
y
I
y
I
x
I
y
2
]
)
[
u
v
]
E(u,v)\approx \lbrack u \quad v\rbrack(\displaystyle\sum_{(x,y)\in W}\omega(x,y) \begin{bmatrix} I_x^2 & I_xI_y \\ I_yI_x & I_y^2 \end{bmatrix}){u\brack v}
E(u,v)≈[uv]((x,y)∈W∑ω(x,y)[Ix2IyIxIxIyIy2])[vu]。
我们将中间括号里面的部分称为自相关系数矩阵A。之后,对角点特征的分析就转换为了对自相关系数矩阵A的分析。
A
=
∑
(
x
,
y
)
∈
W
ω
(
x
,
y
)
[
I
x
2
I
x
I
y
I
y
I
x
I
y
2
]
A=\displaystyle\sum_{(x,y)\in W}\omega(x,y) \begin{bmatrix} I_x^2 & I_xI_y \\ I_yI_x & I_y^2 \end{bmatrix}
A=(x,y)∈W∑ω(x,y)[Ix2IyIxIxIyIy2]
我们的目标:寻找像素点,该像素点无论在哪个方向上,SSD都会有很大的值。即对于角点,
I
x
I_x
Ix和
I
y
I_y
Iy的变化范围都很大。对于平坦区域,
I
x
I_x
Ix和
I
y
I_y
Iy的变化范围都很小。
我们分析
E
(
u
,
v
)
E(u,v)
E(u,v)的形式可得,
E
(
u
,
v
)
E(u,v)
E(u,v)随
(
u
,
v
)
(u,v)
(u,v)而变化,其值紧和A有关,故我们需要研究A是否存在某种特性,使得
(
u
,
v
)
(u,v)
(u,v)在某个局部区域变化时,
E
(
u
,
v
)
E(u,v)
E(u,v)都能达到很大的值。
A进一步等于:
A
=
[
A
1
,
1
A
1
,
2
A
2
,
1
A
2
,
2
]
A=\begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \end{bmatrix}
A=[A1,1A2,1A1,2A2,2]
SSD化为二次型的标准型,其中
λ
1
\lambda_1
λ1和
λ
2
\lambda_2
λ2为特征向量:
E
(
u
,
v
)
=
[
u
v
]
A
[
u
v
]
=
[
u
′
v
′
[
λ
1
0
0
λ
2
]
]
[
u
′
v
′
]
E(u,v)=\lbrack u \quad v\rbrack A{u\brack v}=\lbrack u' \quad v' \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}\rbrack {u'\brack v'}
E(u,v)=[uv]A[vu]=[u′v′[λ100λ2]][v′u′]
令
E
(
u
,
v
)
E(u,v)
E(u,v)为常数,得到该标准型的椭圆形式,其中二次方项的系数分别为
λ
1
\lambda_1
λ1和
λ
2
\lambda_2
λ2,因此得到椭圆的形状为(设较大的特征值为
λ
m
a
x
\lambda_{max}
λmax,较小的特征值为
λ
m
i
n
\lambda_{min}
λmin):
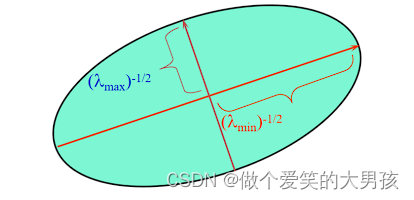
当
(
u
,
v
)
(u,v)
(u,v)沿着
λ
m
a
x
\lambda_{max}
λmax表示的方向变化时,可以用最快速度达到我们设定的
E
(
u
,
v
)
E(u,v)
E(u,v)常数,当
(
u
,
v
)
(u,v)
(u,v)沿着
λ
m
i
n
\lambda_{min}
λmin表示的方向变化时,会以最慢的速度达到我们设定的
E
(
u
,
v
)
E(u,v)
E(u,v)常数。
现在我们恢复
E
(
u
,
v
)
E(u,v)
E(u,v)的自由变化,
E
(
u
,
v
)
E(u,v)
E(u,v)的值是一个随着
u
u
u和
v
v
v变化时也在变化的值了。当两个
λ
\lambda
λ越大时,
u
u
u和
v
v
v变大后
E
(
u
,
v
)
E(u,v)
E(u,v)才会越大。因此我们希望
λ
m
i
n
\lambda_{min}
λmin和
λ
m
a
x
\lambda_{max}
λmax都要足够大才可以。
- 当特征值都很大时, I x I_x Ix和 I y I_y Iy在各个方向都能快速变到很大。我们可以想象出,图像在x方向和y方向整体变化都很大,因此这就是个角点。
- 当特征值一个很大一个很小时, I x I_x Ix或 I y I_y Iy只在某个方向能快速变到很大,我们可以想象出,图像仅在某个方向变化很大,因此这就是边缘区域。
- 当特征值都很小时,该局部区域里
I
x
I_x
Ix和
I
y
I_y
Iy都很小,因此这属于平坦区域,没有特征点。
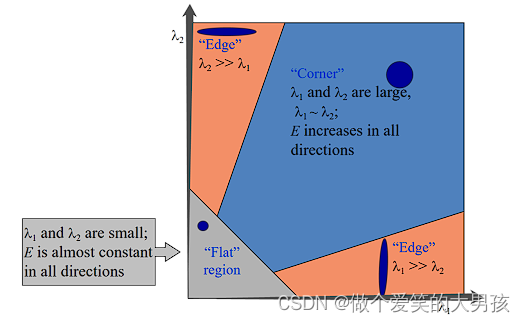
使用特征值判断角点不是很方便,因此定义角点响应函数R: R = λ 1 λ 2 − k ( λ 1 + λ 2 ) 2 = d e t ( M ) − k ( t r a c e ( M ) ) 2 R=\lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2=det(M)-k(trace(M))^2 R=λ1λ2−k(λ1+λ2)2=det(M)−k(trace(M))2
det表示矩阵求行列式的值,trace表示矩阵的迹。 k k k一般取值(0.04-0.06)。
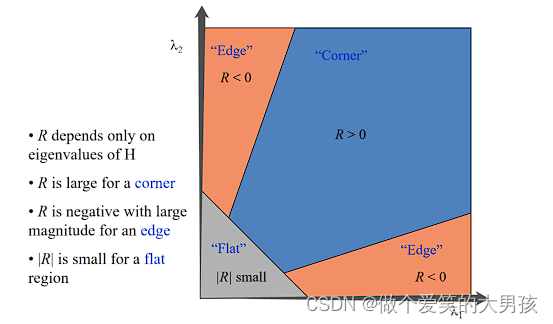
我们检测出来以后可以对所有角点的R响应进行排序,得到R值最大的n个角点作为特征点;以及对一个局部区域取R最大值作为角点。
上面的计算过程中我们会计算图像的梯度,在实际运算中,图像梯度的计算经常会使用Sobel算子对一个局部区域3x3进行卷积。
S o b l e x Soble_x Soblex和 S o b e l y Sobel_y Sobely分别是卷积核:
S o b e l x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] Sobel_x=\begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} Sobelx= −1−2−1000121
S o b e l y = [ 1 2 1 0 0 0 − 1 − 2 − 1 ] Sobel_y=\begin{bmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix} Sobely= 10−120−210−1
通过卷积操作,这样我们就可以得到 I x I_x Ix和 I y I_y Iy,之后再得到每个像素处的 I x 2 、 I y 2 、 I x I y I_x^2、I_y^2、I_xI_y Ix2、Iy2、IxIy,然后对这些图像进行高斯卷积。
最后根据它们计算R响应值就行了。
程序代码
int main()
{
cv::Mat src = cv::imread("triangle.png");
cv::Mat gray;
cv::cvtColor(src, gray, CV_BGR2GRAY);
cv::Mat dst = cv::Mat::zeros(gray.size(), CV_32FC1);
//角点检测代码
cv::cornerHarris(gray, dst, 2, 3, 0.04, BORDER_DEFAULT);
//将dst内的值归一化到(0-255)之间(浮点数)
cv::normalize(dst, dst, 0, 255, NORM_MINMAX, CV_32FC1, cv::Mat());
//上面得到的浮点数缩放为8位uchar类型
cv::convertScaleAbs(dst, dst);
cv::Mat result = src.clone();
//角点检测结果
for (int r = 0; r < result.rows; r++)
{
uchar * curRow = dst.ptr(r);
for (int c = 0; c < result.cols; c++)
{
if ((int)*curRow > 150)
{
cv::circle(result, cv::Point(c, r), 10, cv::Scalar(0, 255, 0), 2, 1, 0);
}
curRow++;
}
}
cv::imshow("input", src);
cv::imshow("output", result);
cv::waitKey(0);
cv::destroyAllWindows();
return 0;
}
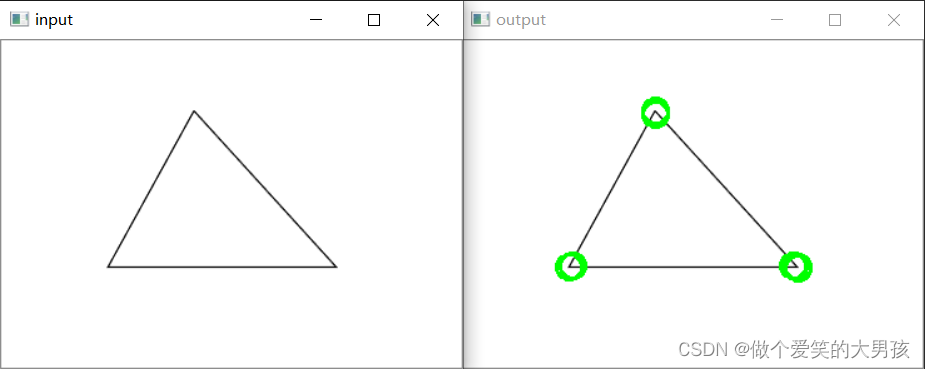
结果展示:
void cv::cornerHarris (InputArray src,
OutputArray dst,
int blockSize,
int ksize,
double k,
int borderType = BORDER_DEFAULT
)
src:单通道的八位或者浮点型图像
dst:存储harris检测结果的图像,大小和src一样,类型位CV_32FC1
blockSize:邻域的大小。也就是上文中窗口的大小。
ksize:Sobel核的大小
k:就是我们在计算R时的k值
borderType:边界扩展的方法。因为在对每一个像素做Sobel操作时,涉及到边界的像素填充。
参考文章:https://dezeming.top/
https://docs.opencv.org/
https://senitco.github.io/2017/06/18/image-feature-harris/






















 807
807











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








