【机器学习与差分隐私代码实现】差分隐私代码实现系列（十二）

写在前面的话

书上学来终觉浅，绝知此事要躬行。

回顾

1、稀疏向量技术对数据集上的敏感度为1的查询流进行操作。它释放流中第一个通过测试的查询的标识，而不是其他任何内容。SVT的优点是，无论考虑多少查询，它都会产生固定的总隐私成本。

2、 在这种情况下，我们希望通过放弃对明显低于阈值的查询的数字答案，而仅报告这些查询确实低于阈值，从而获得本质的分析。（如果我们这样选择的话，我们也将能够获得阈值以上查询的数字值，而只需花费额外的费用）。该技术很简单：添加噪音并仅报告噪声值是否超过阈值。

3、该AboveThreshold算法通过有时返回错误的索引来保护差分隐私。有时，返回的索引可能用于结果未超过阈值的查询，有时，索引可能不是查询结果超过阈值的第一个索引。

4、为什么AboveThreshold做得更好？正如我们在指数机制中看到的那样，顺序组合将允许AboveThreshold发布比实际信息更多的信息。特别是，我们的算法的朴素版本可以释放每个超过阈值的查询的索引（不仅仅是第一个查询），加上嘈杂的查询答案本身，并且它仍然可以保留$nϵ$-差分隐私。AboveThreshold隐瞒所有这些信息的事实允许对隐私成本进行更严格的分析。

机器学习与差分隐私

机器学习与差分隐私（认证鲁棒性和隐私保护）这篇博客中对两者之间的关系和发展进行了恰当的描述，大家感兴趣可以去看看。

《Deep Learning with Differential Privacy》中的MA也有不少博客对其进行分析，这里我也不多赘述。这篇博客主要是想通过代码从本质上来谈一谈机器学习和差分隐私之间的联系，而不是仅仅停留在论文中。

在本篇博客中，我们将探讨如何构建差分隐私机器学习分类器。

将重点介绍一种监督学习问题：给定一组标记的训练示例 { ( x 1 , y 1 ) , … , ( x n , y n ) } \{(x_1, y_1), \dots, (x_n, y_n)\} {(x1​,y1​),…,(xn​,yn​)}，其中$x_i$称为特征向量，$y_i$称为标签，训练一个模型$\theta$，该模型可以预测训练集中不存在的新特征向量的标签。

每个$x_i$ 通常都是描述训练示例特征的实数向量，并且$y_i$ 是从一组预定义的类（通常表示为整数）中提取的，可以从中得出示例。二进制分类器有两个类（通常为 1 和 0，或 1 和 -1）。

使用 Scikit-Learn 进行逻辑回归

为了训练模型，我们将使用一些可用的数据来构建一组训练示例（如前所述），但我们也会留出一些数据作为测试示例。

训练模型后，我们想知道它在训练集中不存在的示例上的工作效果如何，即在以前从未见过的新示例上效果良好的模型可以很好地进行分析。一个不能很好地进行分析的模型已经过度拟合了训练数据。

为了测试泛化，我们将使用测试示例，我们为它们提供了标签，因此我们可以通过要求模型对每个样本进行分类，然后将预测的类与数据集中的实际标签进行比较来测试模型的泛化准确性。

我们将数据拆分为包含 80% 示例的训练集和包含 20% 示例的测试集。

数据集如下：

划分过程如下：

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import pandas as pd
import numpy as np
from collections import defaultdict

# Some useful utilities

def laplace_mech(v, sensitivity, epsilon):
    return v + np.random.laplace(loc=0, scale=sensitivity / epsilon)

def gaussian_mech(v, sensitivity, epsilon, delta):
    return v + np.random.normal(loc=0, scale=sensitivity * np.sqrt(2*np.log(1.25/delta)) / epsilon)

def gaussian_mech_vec(v, sensitivity, epsilon, delta):
    return v + np.random.normal(loc=0, scale=sensitivity * np.sqrt(2*np.log(1.25/delta)) / epsilon, size=len(v))

def pct_error(orig, priv):
    return np.abs(orig - priv)/orig * 100.0

def z_clip(xs, b):
    return [min(x, b) for x in xs]

def g_clip(v):
    n = np.linalg.norm(v, ord=2)
    if n > 1:
        return v / n
    else:
        return v

training_size = int(X.shape[0] * 0.8)

X_train = X[:training_size]
X_test = X[training_size:]

y_train = y[:training_size]
y_test = y[training_size:]

y_test.shape

构建二元分类器的一种简单方法是使用逻辑回归。

scikit-learn 库有一个用于执行逻辑回归的内置模块，称为LogisticRegression，并且很容易使用我们的数据构建模型。

from sklearn.linear_model import LogisticRegression
model = LogisticRegression().fit(X_train,y_train)
model

接下来，我们可以使用模型的predict方法预测测试集的标签。

model.predict(X_test)

那么，我们的模型正确了多少个测试示例呢？我们可以将预测的标签与数据集中的实际标签进行比较;如果我们将正确预测的标签数量除以测试示例的总数，我们可以测量正确分类的示例的百分比。

np.sum(model.predict(X_test) == y_test)/X_test.shape[0]

我们的模型为测试集中 84% 的示例预测了正确的标签。对于此数据集，这是一个相当不错的结果。

什么是模型？

模型到底是什么？它如何编码用于进行预测的信息？

有许多不同类型的模型，但我们将在这里探讨的是线性模型。对于具有$k$维特征向量$x_1,\dots ,x_k$的未标记示例，线性模型通过首先计算数量来预测标签：

$$w_1{x}_1+\cdots +w_k{x}_k+bias$$
然后取它的符号（即，如果上面的数量为负，我们预测标签-1;如果它是正的，我们预测1）。

然后，模型本身可以由包含值$w_1,\dots ,w_k$和$bias$值的向量表示。该模型被称为线性的，因为我们在预测标签时计算的数量是1次的多项式（即线性）。值$w_1,\dots ,w_k$ 通常称为模型的权重或系数，$bias$通常称为偏差项或截距。

这实际上也是scikit-learn表示其逻辑回归模型的方式！我们可以使用模型的coef_属性来检查已训练模型的权重：

model.intercept_[0], model.coef_[0]

请注意，我们将始终具有与特征$x_i$完全相同的权重数量$w_i$，因为我们必须将每个特征乘以相应的权重。这意味着我们的模型具有与我们的特征向量完全相同的维度。

现在我们有了一种方法来获取权重和偏差项，我们可以实现自己的函数来执行预测：

def predict(xi, theta, bias=0):
    label = np.sign(xi @ theta + bias)
    return label

np.sum(predict(X_test, model.coef_[0], model.intercept_[0]) == y_test)/X_test.shape[0]

我们在这里将偏差术语设置为可选，因为在许多情况下，没有它也可以做得很好。为了让事情变得更简单，我们不会费心在自己的算法中训练偏差项。

使用梯度下降训练模型

训练过程实际上是如何运作的？scikit-learn库有一些非常复杂的算法，但我们也可以通过实现一个简单的称为梯度下降的算法来做到这一点。

**大多数机器学习的训练算法都是根据损失函数定义的，它指定了一种测量模型在预测时有多"坏"的方法。**训练算法的目标是最小化损失函数的输出，具有低损失的模型将擅长预测。

机器学习领域已经开发了许多不同的常用损失函数。对于每个正确预测的示例，简单的损失函数可能返回 0，对于每个错误预测的示例返回 1;当损失变为 0 时，这意味着我们已经正确预测了每个示例的标签。

二元分类中比较常用的损失函数称为逻辑损失，逻辑损失为我们提供了一个衡量标准，即我们距离预测正确标签还有多远（这比简单的0 vs 1方法更具信息性）。

逻辑损失由以下 Python 函数实现：

def loss(theta, xi, yi):
    exponent = - yi * (xi.dot(theta))
    return np.log(1 + np.exp(exponent))

我们可以使用损失函数来衡量特定模型的好坏。让我们用一个权重都为零的模型来尝试一下。这个模型不太可能很好地工作，但它是一个起点，我们可以从中训练出更好的模型。

theta = np.zeros(X_train.shape[1])
loss(theta, X_train[0], y_train[0])

我们通常通过简单地对训练数据中所有示例的损失进行平均来衡量我们的模型在整个训练集上有多好。

在本例中，我们弄错了每个示例，因此整个训练集上的平均损失正好等于我们上面计算的损失，仅举一例。

np.mean([loss(theta, x_i, y_i) for x_i, y_i in zip(X_train, y_train)])

我们训练模型的目标是将损失降至最低。所以关键问题是：我们如何修改模型以减小损失？

梯度下降是一种通过根据损失的梯度更新模型来使损失变小的方法。

梯度就像一个多维导数：对于具有多维输入的函数（如上面的损失函数），梯度体现函数的输出相对于输入的每个维度的变化速度。

如果梯度在特定维度中为正，则意味着如果我们增加该维度的模型权重，则该函数的值将增加;我们希望损失减少，因此我们应该通过朝着梯度的反方向来修改我们的模型，即做与梯度相反的事情。由于我们沿梯度相反的方向移动模型，因此这称为梯度下降。

当我们迭代地执行这个下降过程的许多步骤时，我们慢慢地越来越接近模型，从而最大限度地减少损失。此算法称为梯度下降。让我们看看这在Python中看起来如何;首先，我们将定义梯度函数。

def gradient(theta, xi, yi):
    exponent = yi * (xi.dot(theta))
    return - (yi*xi) / (1+np.exp(exponent))

梯度下降的单一步骤

接下来，让我们执行梯度下降的单个步骤。我们可以将gradient函数应用于训练数据中的单个示例，这应该为我们提供足够的信息来改进该示例的模型。我们通过从当前theta模型中减去梯度来"下降"梯度。

theta = theta - gradient(theta, X_train[0], y_train[0])
theta

现在，如果我们从训练数据中调用相同的示例，则其标签被正确预测！这意味着我们的更新确实改进了模型，因为它现在能够对此示例进行分类。

y_train[0], predict(theta, X_train[0])

我们将多次测量模型的准确性，因此让我们定义一个用于测量准确性的帮助器函数。它的工作方式与上述 sklearn 模型的精度测量相同。我们可以通过降低一个示例的梯度来使用它在theta上，看看我们的模型在测试集上有多好。

def accuracy(theta):
    return np.sum(predict(X_test, theta) == y_test)/X_test.shape[0]

accuracy(theta)

我们改进的模型现在可以正确预测测试集的 75% 的标签！这是一个很好的进步，我们已经大大改进了模型。

梯度下降算法

我们需要进行两项更改才能得出基本的梯度下降算法。首先，我们上面的单个步骤仅使用了训练数据中的单个示例;我们希望在更新模型时考虑整个训练集，以便改进所有示例的模型。其次，我们需要执行多次迭代，以尽可能接近最小化损失。

**我们可以通过计算所有训练示例的平均梯度来解决第一个问题，并将其用于下降步骤，而不是我们之前使用的单例梯度。**我们的avg_grad函数计算整个训练示例数组和相应标签的平均梯度。

def avg_grad(theta, X, y):
    grads = [gradient(theta, xi, yi) for xi, yi in zip(X, y)]
    return np.mean(grads, axis=0)

avg_grad(theta, X_train, y_train)

为了解决第二个问题，我们将定义一个迭代算法，该算法将梯度降序多次。

def gradient_descent(iterations):
    theta = np.zeros(X_train.shape[1])

    for i in range(iterations):
        theta = theta - avg_grad(theta, X_train, y_train)

    return theta

theta = gradient_descent(10)
accuracy(theta)

经过10次迭代，我们的模型达到了近78%的准确率，还不错！

我们的梯度下降算法看起来很简单（确实如此！）但不要让它的简单性愚弄你，这种基本方法是最近在大规模深度学习中取得的许多成功背后的原因，我们的算法在设计上非常接近于在流行的机器学习框架中实现的算法，如Tensorflow。

请注意，我们没有完全达到我们之前训练的 sklearn 模型的 84% 准确率。别担心，我们的算法绝对有能力做到这一点！我们只需要更多的迭代，以接近最小的损失。

通过100次迭代，我们越来越接近82%的准确率。

但是，当我们要求如此多的迭代时，该算法需要很长时间才能运行。更糟糕的是，我们越接近最小化损失，就越难改进，所以我们在100次迭代后可能会达到82%的准确率，但可能需要1000次迭代才能达到84%。

这指出了机器学习的根本紧张关系，**一般来说，更多的训练迭代可以提高准确性，但更多的迭代需要更多的计算时间。**大多数用于使大规模深度学习变得实用的"技巧"实际上都是为了加快梯度下降的每次迭代，以便在相同的时间内执行更多的迭代。

还有一件有趣的事情需要注意：损失函数的值确实会随着我们执行的梯度下降的每次迭代而下降 。

因此，随着我们执行更多的迭代，我们慢慢地接近最小化损失。另请注意，训练和测试损失彼此非常接近，这表明我们的模型不会过度拟合训练数据。

def gradient_descent_log(iterations):
    theta = np.zeros(X_train.shape[1])

    for i in range(iterations):
        theta = theta - avg_grad(theta, X_train, y_train)
        print(f'Training loss: {np.mean(loss(theta, X_train, y_train))}')
        print(f'Testing loss: {np.mean(loss(theta, X_test, y_test))}\n')

    return theta

gradient_descent_log(5);

梯度下降与差分隐私

我们如何使上述算法差分隐私？我们希望设计一种算法来确保训练数据的差分隐私，以便最终模型不会显示有关单个训练示例的任何信息。

算法中唯一使用训练数据的部分是梯度计算。使算法具有差分隐私的一种方法是在每次迭代时在更新模型之前向梯度本身添加噪声。这种方法通常称为噪声梯度下降，因为我们直接将噪声添加到梯度中。

我们的梯度函数是一个向量值函数，因此我们可以使用gaussian_mech_vec它来向其输出添加噪声：

def noisy_gradient_descent(iterations, epsilon, delta):
    theta = np.zeros(X_train.shape[1])
    sensitivity = '???'

    for i in range(iterations):
        grad = avg_grad(theta, X_train, y_train)
        noisy_grad = gaussian_mech_vec(grad, sensitivity, epsilon, delta)
        theta = theta - noisy_grad

    return theta

上面的代码只缺少一个部分，**梯度函数的灵敏度是多少？**回答这个问题是算法工作的核心困难。

这里有两个主要挑战。

首先，梯度是平均查询的结果，它是每个示例的许多梯度的平均值。

正如我们之前所看到的，最好将此类查询拆分为总和查询和计数查询。这并不难做到，我们可以计算每个示例梯度的总和，而不是它们的平均值，并在以后除以噪声计数。

其次，我们需要绑定每个示例梯度的灵敏度。

有两种基本方法：我们可以分析梯度函数本身（就像我们在之前的查询中所做的那样）来确定其最坏情况下的全局灵敏度，或者我们可以通过剪裁梯度函数的输出来强制执行灵敏度（就像我们在样本和聚合中所做的那样）。

我们将从第二种方法开始，通常称为渐变剪切 。因为它在概念上更简单，并且在其应用程序中更通用。

渐变剪切

回想一下，当我们实现采样和聚合时，我们通过剪裁其输出，对灵敏度未知的函数$f$强制执行所需的灵敏度。$f$的敏感度为：

$$|f(x)-f(x^{\prime })|$$
使用参数$b$进行剪裁后，这将变为：

$$|\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(f(x),b)-\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(f(x^{\prime }),b)|$$
在最坏的情况下，$\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(f(x),b)=b$和$\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(f(x^{\prime }),b)=0$，因此裁剪结果的灵敏度正好是$b$（剪裁参数的值）。

我们可以使用相同的技巧来绑定梯度函数的L2灵敏度。

我们需要定义一个函数来"裁剪"向量，使其在所需范围内具有 L2 范数。我们可以通过缩放向量来实现这一点：如果我们按元素除以向量的L2范数，那么生成的向量的L2范数将为1。

如果我们想针对特定的剪切参数$b$，我们可以将缩放的向量乘以$b$以将其放大以具有 L2 范数$b$。

我们希望避免修改已经将 L2 范数低于$b$的向量;在这种情况下，我们只返回原始向量。我们可以与参数ord=2一起使用np.linalg.norm来计算向量的 L2 范数。

def L2_clip(v, b):
    norm = np.linalg.norm(v, ord=2)
    
    if norm > b:
        return b * (v / norm)
    else:
        return v

现在，我们已准备好分析裁剪渐变的灵敏度。我们将梯度表示为$\nabla (\theta ;X,y)$（对应于我们的 Python 代码gradient）：

$$\Vert \mathsf{L}2\_\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(\nabla (\theta ;X,y),b)-\mathsf{L}2\_\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(\nabla (\theta ;X^{\prime },y)){\Vert }_2$$
在最坏的情况下，$\mathsf{L}2\_\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(\nabla (\theta ;X,y),b)$的 L2 范数为$b$和$\mathsf{L}2\_\mathsf{c}\mathsf{l}\mathsf{i}\mathsf{p}(\nabla (\theta ;X^{\prime },y))$全为零 - 因此差分的 L2 范数等于$b$。因此，剪切渐变的 L2 灵敏度受剪切参数$b$的限制！

现在，我们可以继续计算裁剪梯度的总和，并根据我们通过裁剪强制执行的 L2 灵敏度$b$添加噪声。

def gradient_sum(theta, X, y, b):
    gradients = [L2_clip(gradient(theta, x_i, y_i), b) for x_i, y_i in zip(X,y)]

    return np.sum(gradients, axis=0)

现在，我们已准备好完成噪声梯度下降算法。要计算噪声平均梯度，我们需要：

1、根据噪声的灵敏度将噪声添加到梯度的总和中$b$

2、计算训练示例数的噪声计数（灵敏度 1）

3、将 （1） 中的噪声和除以 （2） 中的噪声计数

def noisy_gradient_descent(iterations, epsilon, delta):
    theta = np.zeros(X_train.shape[1])
    sensitivity = 5.0
    
    noisy_count = laplace_mech(X_train.shape[0], 1, epsilon)

    for i in range(iterations):
        grad_sum        = gradient_sum(theta, X_train, y_train, sensitivity)
        noisy_grad_sum  = gaussian_mech_vec(grad_sum, sensitivity, epsilon, delta)
        noisy_avg_grad  = noisy_grad_sum / noisy_count
        theta           = theta - noisy_avg_grad

    return theta
 
theta = noisy_gradient_descent(10, 0.1, 1e-5)
accuracy(theta)

此算法的每次迭代都满足$(ϵ,\delta )$-差分隐私，我们执行一个额外的查询来确定满足$ϵ$-差分隐私的噪声计数。

如果我们执行$k$迭代，则通过顺序组合，算法满足$(kϵ+ϵ,k\delta )$-差分隐私。我们还可以使用高级组合来分析总隐私成本;更好的是，我们可以将算法转换为 Rényi 差分隐私或零集中差分隐私，并获得隐私成本的严格限制。

梯度的灵敏度

我们之前的方法非常通用，因为它不对梯度的行为做出任何假设。

然而，有时我们确实对梯度的行为有所了解。特别是，一大类有用的梯度函数（包括我们在这里使用的逻辑损失的梯度）是利普希茨连续，这意味着它们具有有界的全局灵敏度。从形式上讲，可以证明：

$$\text{If}\Vert x_i{\Vert }_2\le b\text{then}\Vert \nabla (\theta ;x_i,y_i){\Vert }_2\le b$$
这一事实允许我们裁剪训练示例的值（即梯度函数的输入），而不是梯度函数的输出，并获得梯度的L2灵敏度的边界。

裁剪训练示例而不是梯度有两个优点。首先，估计训练数据的比例（从而选择一个好的裁剪参数）通常比估计训练期间将要计算的梯度的尺度更容易。

其次，它在计算上更有效：我们可以裁剪一次训练示例，并在每次训练模型时重用裁剪的训练数据。使用渐变剪切，我们需要在训练期间修剪每个梯度。

此外，我们不再被迫计算每个示例的梯度，以便我们可以裁剪它们，相反，我们可以一次计算所有梯度，这可以非常有效地完成（这是机器学习中常用的技巧，但我们不会在这里讨论它）。

但请注意，许多有用的损失函数，特别是那些从深度学习中的神经网络派生的函数，没有有界的全局灵敏度。对于这些损耗函数，我们被迫使用渐变裁剪。

我们可以通过对算法进行一些简单的修改来裁剪训练示例而不是梯度。首先，我们在开始训练之前使用L2_clip裁剪训练示例。其次，我们只需删除用于裁剪渐变的代码即可。

def gradient_sum(theta, X, y, b):
    gradients = [gradient(theta, x_i, y_i) for x_i, y_i in zip(X,y)]

    return np.sum(gradients, axis=0)
def noisy_gradient_descent(iterations, epsilon, delta):
    theta = np.zeros(X_train.shape[1])
    sensitivity = 5.0
    
    noisy_count = laplace_mech(X_train.shape[0], 1, epsilon)
    clipped_X = [L2_clip(x_i, sensitivity) for x_i in X_train]

    for i in range(iterations):
        grad_sum        = gradient_sum(theta, clipped_X, y_train, sensitivity)
        noisy_grad_sum  = gaussian_mech_vec(grad_sum, sensitivity, epsilon, delta)
        noisy_avg_grad  = noisy_grad_sum / noisy_count
        theta           = theta - noisy_avg_grad

    return theta
    
theta = noisy_gradient_descent(10, 0.1, 1e-5)
accuracy(theta)

可以对该算法进行许多改进，这可以提高隐私成本和准确性。许多都来自机器学习文献。一些示例包括：

1、通过将每次迭代$ϵ$作为算法的一部分，将总隐私成本限定为$ϵ$。

2、通过高级组合定理、RDP 或 zCDP 为大量迭代提供更好的组合。

3、小型分组：使用一小部分训练数据而不是整个训练集来计算每次迭代的梯度（这减少了计算梯度所需的计算）。

4、与minibatching相结合的平行组合定理。

5、随机抽样批次与小批次相结合。

6、其他超参数，如学习速率$\eta$。

噪音对训练的影响

到目前为止，我们已经看到迭代次数对我们获得的模型的准确性有很大的影响，因为更多的迭代可以让你更接近最小的损失。

由于我们的差分隐私算法会在梯度上增加噪声，这也会影响准确性，噪声会导致我们的算法在训练期间向错误的方向移动，并且实际上会使模型变得更糟。

可以合理地预期，$ϵ$的值越小，模型的精度就越低（因为这是我们迄今为止看到的每个差分隐私算法的趋势）。

这是事实，但也有一个稍微更微妙的权衡，这是由于我们在执行算法的多次迭代时需要考虑的组成：更多的迭代意味着更大的隐私成本。

在标准梯度下降算法中，迭代次数越多，通常会产生更好的模型。在我们的差分隐私版本中，更多的迭代可能会使模型变得更糟，因为我们必须为每次迭代使用较小的$ϵ$，因此噪声的规模会上升。在差分隐私机器学习中，在使用的迭代次数和添加的噪声规模之间取得适当的平衡是很重要的（有时是非常具有挑战性的）。

让我们做一个小实验，看看$ϵ$ 的设置如何影响模型的准确性。我们将为$ϵ$的多个值训练一个模型，每次使用 20 次迭代，并根据训练时使用的$ϵ$值绘制每个模型的准确性图。

delta = 1e-5

epsilons = [0.001, 0.003, 0.005, 0.008, 0.01, 0.03, 0.05, 0.08, 0.1]
thetas   = [noisy_gradient_descent(10, epsilon, delta) for epsilon in epsilons]
accs     = [accuracy(theta) for theta in thetas]
plt.xlabel('Epsilon')
plt.ylabel('Accuracy')
plt.plot(epsilons, accs);

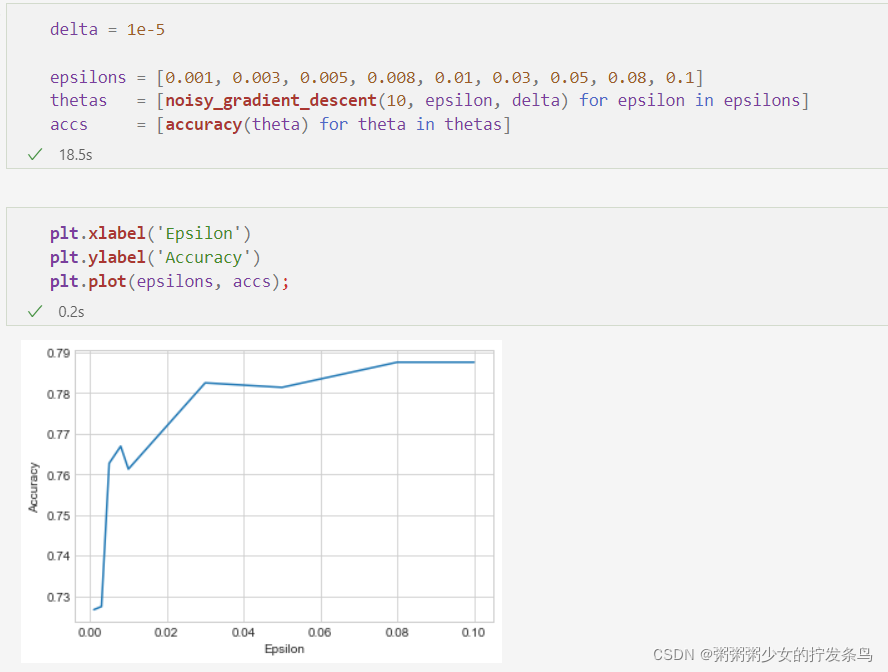
该图显示，$ϵ$的非常小的值会导致模型的精度大大降低。请记住，我们在绘图中指定的$ϵ$是每次迭代$ϵ$，因此组合后的隐私成本要高得多。

总结

1、梯度下降是一种通过根据损失的梯度更新模型来使损失变小的方法。梯度就像一个多维导数：对于具有多维输入的函数（如上面的损失函数），梯度体现函数的输出相对于输入的每个维度的变化速度。如果梯度在特定维度中为正，则意味着如果我们增加该维度的模型权重，则该函数的值将增加;我们希望损失减少，因此我们应该通过朝着梯度的反方向来修改我们的模型，即做与梯度相反的事情。由于我们沿梯度相反的方向移动模型，因此这称为梯度下降。

2、一般来说，更多的训练迭代可以提高准确性，但更多的迭代需要更多的计算时间。大多数用于使大规模深度学习变得实用的"技巧"实际上都是为了加快梯度下降的每次迭代，以便在相同的时间内执行更多的迭代。

3、我们的目的是使得最终模型不会显示有关单个训练示例的任何信息。算法中唯一使用训练数据的部分是梯度计算。使算法具有差分隐私的一种方法是在每次迭代时在更新模型之前向梯度本身添加噪声。这种方法通常称为噪声梯度下降，因为我们直接将噪声添加到梯度中。

4、这里有两个主要挑战。首先，梯度是平均查询的结果，它是每个示例的许多梯度的平均值。正如我们之前所看到的，最好将此类查询拆分为总和查询和计数查询。这并不难做到，我们可以计算每个示例梯度的总和，而不是它们的平均值，并在以后除以噪声计数。其次，我们需要绑定每个示例梯度的灵敏度。有两种基本方法：我们可以分析梯度函数本身（就像我们在之前的查询中所做的那样）来确定其最坏情况下的全局灵敏度，或者我们可以通过剪裁梯度函数的输出来强制执行灵敏度（就像我们在样本和聚合中所做的那样）。

5、渐变剪裁算法的每次迭代都满足$(ϵ,\delta )$-差分隐私，我们执行一个额外的查询来确定满足$ϵ$-差分隐私的噪声计数。如果我们执行$k$迭代，则通过顺序组合，算法满足$(kϵ+ϵ,k\delta )$-差分隐私。我们还可以使用高级组合来分析总隐私成本;更好的是，我们可以将算法转换为 Rényi 差分隐私或零集中差分隐私，并获得隐私成本的严格限制。

6、我们之前的方法非常通用，因为它不对梯度的行为做出任何假设。然而，有时我们确实对梯度的行为有所了解。特别是，一大类有用的梯度函数（包括我们在这里使用的逻辑损失的梯度）是利普希茨连续，这意味着它们具有有界的全局灵敏度。

7、裁剪训练示例而不是梯度有两个优点。首先，估计训练数据的比例（从而选择一个好的裁剪参数）通常比估计训练期间将要计算的梯度的尺度更容易。其次，它在计算上更有效：我们可以裁剪一次训练示例，并在每次训练模型时重用裁剪的训练数据。使用渐变剪切，我们需要在训练期间修剪每个梯度。此外，我们不再被迫计算每个示例的梯度，以便我们可以裁剪它们，相反，我们可以一次计算所有梯度，这可以非常有效地完成（这是机器学习中常用的技巧，但我们不会在这里讨论它）。

8、可以合理地预期，$ϵ$的值越小，模型的精度就越低（因为这是我们迄今为止看到的每个差分隐私算法的趋势）。这是事实，但也有一个稍微更微妙的权衡，这是由于我们在执行算法的多次迭代时需要考虑的组成：更多的迭代意味着更大的隐私成本。在标准梯度下降算法中，迭代次数越多，通常会产生更好的模型。在我们的差分隐私版本中，更多的迭代可能会使模型变得更糟，因为我们必须为每次迭代使用较小的$ϵ$，因此噪声的规模会上升。在差分隐私机器学习中，在使用的迭代次数和添加的噪声规模之间取得适当的平衡是很重要的（有时是非常具有挑战性的）。