【差分隐私和数据的适配性】差分隐私代码实现系列（十四）

最新推荐文章于 2025-05-07 14:29:02 发布

粥粥粥少女的拧发条鸟

最新推荐文章于 2025-05-07 14:29:02 发布

阅读量2.2k

点赞数

分类专栏：差分隐私文章标签：机器学习人工智能算法

本文链接：https://blog.csdn.net/qq_41691212/article/details/122906066

版权

差分隐私专栏收录该内容

38 篇文章

订阅专栏

差分隐私代码实现系列（十四）

写在前面的话
回顾
合成数据
直方图
添加差分隐私
生成表格数据
生成更多列
总结

写在前面的话

书上学来终觉浅，绝知此事要躬行。

回顾

1、本地模型也有一个明显的缺点：在中心差分隐私下，对于与相同查询相同的隐私成本，本地模型中查询结果的准确性通常要低几个数量级。这种准确性的巨大损失意味着只有少数查询类型适用于本地差分隐私，即使对于这些查询类型，也需要大量的参与者。

2、当答案本身较小时，本地模型的误差会变大。在误差上，随机响应比中心模型中的拉普拉斯机制差几个数量级。即使本地模型有更好的算法，但是在提交数据之前必须添加噪声的固有局限性意味着本地模型算法的准确性始终比最佳中心模型算法差。

3、已经提出了用于在本地模型中执行直方图查询的其他方法，包括前面论文中详细介绍的一些方法。这些可以在一定程度上提高准确性，但是在局部模型中必须确保每个样本的差分隐私的基本限制意味着，即使是最复杂的技术也无法与我们在中心模型中看到的机制的准确性相匹配。

合成数据

数据对于隐私保护的重要性不言而喻，什么样的数据能用差分隐私，怎么用成为关键问题之一。

在这篇博文中，将研究使用差分隐私算法生成合成数据的问题。严格来说，这种算法的输入是原始数据集，其输出是具有相同形状（即相同列数和相同行数）的合成数据集。

此外，我们希望合成数据集中的值与原始数据集中的相应值具有相同的属性。

例如，如果我们将美国人口普查数据集作为原始数据，那么我们希望我们的合成数据具有与原始数据相似的参与者年龄分布，并保留列之间的相关性（例如，年龄和职业之间的联系）。

用于生成此类合成数据的大多数算法都依赖于原始数据集的合成表示形式，该表示形式与原始数据不具有相同的形状，但允许回答有关原始数据的查询。

例如，如果我们只关心不同年龄范围的查询，那么我们可以生成一个年龄直方图 - 原始数据中有多少参与者具有每个可能的年龄 - 并使用直方图来回答查询。

此直方图是一种合成表示形式，适用于回答某些查询，但它的形状与原始数据不同，因此它不是合成数据。

某些算法只是使用合成表示形式来回答查询。其他人使用合成表示来生成合成数据。我们将介绍一种合成表示，直方图以及从中生成合成数据的几种方法。

直方图

我们已经看到了许多直方图，它们是差分隐私分析的主要内容，因为可以立即应用并行组合。我们还看到了范围查询的概念，尽管我们并不经常使用该名称。

作为获取合成数据的第一步，我们将为原始数据集的一列设计一个合成表示形式，该列能够回答范围查询。

范围查询计算数据集中值位于给定范围内的行数。例如，"有多少参与者年龄在 21 岁到 33 岁之间？"是一个范围查询。

def range_query(df, col, a, b):
    return len(df[(df[col] >= a) & (adult[col] < b)])

range_query(adult, 'Age', 21, 33)

在这里插入图片描述
我们可以定义一个直方图查询，该查询为0到100之间的每个年龄定义一个直方图条柱，并使用范围查询计算每个条柱中的人数。

结果看起来非常类似于调用plt.hist数据的输出，因为我们基本上是手动计算相同的结果。

bins = list(range(0, 100))
counts = [range_query(adult, 'Age', b, b+1) for b in bins]
plt.xlabel('Age')
plt.ylabel('Number of Occurrences')
plt.bar(bins, counts);

在这里插入图片描述
我们可以将这些直方图结果用作原始数据的合成表示！要回答范围查询，我们可以将属于该范围的条柱的所有计数相加。

def range_query_synth(syn_rep, a, b):
    total = 0
    for i in range(a, b):
        total += syn_rep[i]
    return total
    
range_query_synth(counts, 21, 33)

在这里插入图片描述
请注意，无论我们是对原始数据还是合成表示形式发出范围查询，我们都会得到完全相同的结果。我们没有丢失原始数据集中的任何信息（至少为了回答年龄范围查询的目的）。

添加差分隐私

我们可以很容易地使我们的合成数据满足差分隐私。我们可以将拉普拉斯噪声分别添加到直方图中的每个计数中，通过并行组合，这满足 $\epsilon$ -差分隐私。

epsilon = 1
dp_syn_rep = [laplace_mech(c, 1, epsilon) for c in counts]

我们可以使用与以前相同的函数，使用我们的差分隐私合成表示来回答范围查询。

通过后处理，这些结果还满足 $\epsilon$ -差分隐私。

此外，由于我们依赖于后期处理，因此我们可以根据需要回答任意数量的查询，而不会产生额外的隐私成本。

range_query_synth(dp_syn_rep, 21, 33)

在这里插入图片描述
结果有多准确？对于小范围，我们从合成表示中获得的结果与通过将Laplace机制直接应用于我们要回答的范围查询的结果可以获得的结果具有非常相似的准确性。例如：

true_answer = range_query(adult, 'Age', 30, 31)
print('Synthetic representation error: {}'.format(pct_error(true_answer, range_query_synth(dp_syn_rep, 30, 31))))
print('Laplace mechanism error: {}'.format(pct_error(true_answer, laplace_mech(true_answer, 1, epsilon))))

在这里插入图片描述
随着范围变大，计数越大，因此我们预计误差会有所改善。

我们已经一遍又一遍地看到这一点，更大的组意味着更强的信号，这导致较低的相对误差。

通过拉普拉斯机制，我们正好看到了这种行为。然而，通过我们的合成表示，我们将来自许多较小组的噪声结果加在一起。因此随着信号的增长，噪声也会增加！

因此，无论范围的大小如何，我们在使用合成表示时都会看到大致相同的相对误差大小，与拉普拉斯机制恰恰相反！

true_answer = range_query(adult, 'Age', 30, 71)
print('Synthetic representation error: {}'.format(pct_error(true_answer, range_query_synth(dp_syn_rep, 30, 71))))
print('Laplace mechanism error: {}'.format(pct_error(true_answer, laplace_mech(true_answer, 1, epsilon))))

在这里插入图片描述
这种差异证明了我们的合成表示的缺点：它可以回答它所涵盖范围的任何范围查询，但它可能无法提供与Laplace机制相同的精度。

我们的合成表示的主要优点是能够在没有额外隐私预算的情况下回答无限多个查询，主要缺点是准确性的损失。

生成表格数据

下一步是从我们的合成表示到合成数据。

为此，我们希望将合成表示视为概率分布，该概率分布估计从中获取原始数据的基础分布，并从中抽取样本。因为我们只考虑一个列，而忽略所有其他列，所以这被称为边际分布（特别是单向边际分布【1-way marginal】）。

我们的策略很简单：我们对每个直方图条柱都有计数;我们将对这些计数进行规范化，使它们的总和为 1，然后将它们视为概率。

一旦我们有了这些概率，我们就可以通过随机选择直方图的一个条柱，按概率加权，从它所代表的分布中抽样。我们的第一步是准备计数，方法是确保没有计数为负数，并将它们规范化为 1：

dp_syn_rep_nn = np.clip(dp_syn_rep, 0, None)
syn_normalized = dp_syn_rep_nn / np.sum(dp_syn_rep_nn)
np.sum(syn_normalized)

在这里插入图片描述
请注意，如果我们绘制归一化计数 - 我们现在可以将其视为每个相应直方图条柱的概率，因为它们的总和为1 - 我们看到一个看起来非常像原始直方图的形状（反过来，看起来很像原始数据的形状）。这都是可以预料的 - 除了它们的规模，这些概率只是计数。

plt.xlabel('Age')
plt.ylabel('Probability')
plt.bar(bins, syn_normalized);

在这里插入图片描述
最后一步是根据这些概率生成新样本。我们可以使用np.random.choice，它允许传入与第一个参数中给定的选择相关联的概率列表（在参数中）。它准确地实现了采样任务所需的加权随机选择。我们可以根据需要生成任意数量的样本，而无需额外的隐私成本，因为我们已经将计数设置为差分隐私。

def gen_samples(n):
    return np.random.choice(bins, n, p=syn_normalized)

syn_data = pd.DataFrame(gen_samples(5), columns=['Age'])
syn_data

在这里插入图片描述
我们希望，我们以这种方式生成的样本将根据与原始数据相同的基础分布进行粗略分布。这意味着我们可以使用生成的综合数据来回答使用原始数据可以回答的相同查询。特别是，如果我们在大型合成数据集中绘制年龄直方图，我们将看到与原始数据相同的形状。

syn_data = pd.DataFrame(gen_samples(10000), columns=['Age'])
plt.xlabel('Age')
plt.ylabel('Number of Occurrences')
plt.hist(syn_data['Age'], bins=bins);

在这里插入图片描述
我们还可以回答过去看到的其他查询，例如平均值和范围查询：

print('Mean age, synthetic: {}'.format(np.mean(syn_data['Age'])))
print('Mean age, true answer: {}'.format(np.mean(adult['Age'])))
print('Percent error: {}'.format(pct_error(np.mean(syn_data['Age']), np.mean(adult['Age']))))

在这里插入图片描述

print('Mean age, synthetic: {}'.format(range_query(syn_data, 'Age', 20, 65)))
print('Mean age, true answer: {}'.format(range_query(adult, 'Age', 20, 65)))
print('Percent error: {}'.format(pct_error(range_query(adult, 'Age', 20, 65), 
                                           range_query(syn_data, 'Age', 20, 65))))

在这里插入图片描述
我们的均值查询具有相当低的误差（尽管仍然比我们直接应用拉普拉斯机制所能达到的误差要大得多）。

但是，我们的范围查询有非常大的错误！这仅仅是因为我们没有完全匹配原始数据的形状 - 我们只生成了10，000个样本，而原始数据集有超过30，000行。我们可以执行额外的差异私有查询来确定原始数据中的行数，然后生成具有相同行数的新综合数据集，这将改善我们的范围查询结果。

n = laplace_mech(len(adult), 1, 1.0)
syn_data = pd.DataFrame(gen_samples(int(n)), columns=['Age'])

print('Mean age, synthetic: {}'.format(range_query(syn_data, 'Age', 20, 65)))
print('Mean age, true answer: {}'.format(range_query(adult, 'Age', 20, 65)))
print('Percent error: {}'.format(pct_error(range_query(adult, 'Age', 20, 65), 
                                           range_query(syn_data, 'Age', 20, 65))))

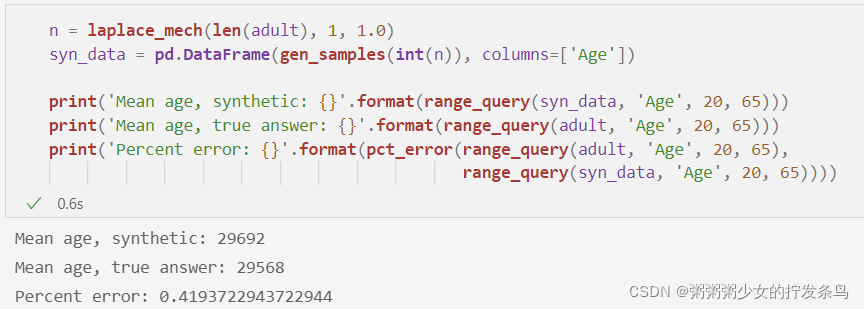
在这里插入图片描述
现在我们看到我们预期的较低误差。

生成更多列

到目前为止，我们已经生成了与原始数据集的行数相匹配的综合数据，并且对于回答有关原始数据的查询非常有用，但它只有一列！我们如何生成更多列？

有两种基本方法。

我们可以对每个 $k$ 列重复上面遵循的过程（生成 $k$ 1 向边际【1-way marginals】），并得出 $k$ 单独的合成数据集，每个数据集都有一列。然后，我们可以将这些数据集分解在一起，以构造具有 $k$ 列的单个数据集。这种方法很简单，但是由于我们孤立地考虑每个列，因此我们将失去原始数据中存在的列之间的相关性。例如，在数据中，年龄和职业可能是相关的（例如，管理人员年龄大于年轻的可能性更大）;如果我们孤立地考虑每一列，我们会得到正确的18岁和经理人数，但我们可能对18岁的经理人数非常错误。

另一种方法是将多个列放在一起考虑。例如，我们可以同时考虑年龄和职业，并计算有多少18岁的经理，有多少19岁的经理，等等。这种修改过程的结果是双向边际分布。我们最终将考虑年龄和职业的所有可能组合 - 这正是我们之前构建应急表时所做的！例如：

ct = pd.crosstab(adult['Age'], adult['Occupation'])
ct.head()

在这里插入图片描述
现在，我们可以完全按照之前的做法 - 在这些计数中添加噪声，然后对它们进行规范化并将它们视为概率！现在，每个计数对应于一对值 - 年龄和职业 - 因此，当我们从构建的分布中采样时，我们将同时获得两个值。

dp_ct = ct.applymap(lambda x: max(laplace_mech(x, 1, 1), 0))
dp_vals = dp_ct.stack().reset_index().values.tolist()
probs = [p for _,_,p in dp_vals]
vals = [(a,b) for a,b,_ in dp_vals]
probs_norm = probs / np.sum(probs)
list(zip(vals, probs_norm))[0]

在这里插入图片描述
检查概率的第一个元素，我们发现我们有0.07%的机会生成代表17岁文书工作者的行。现在，我们已准备好生成一些行！我们将首先在vals列表中生成一个索引列表，然后通过索引到vals;我们必须这样做，因为np.random.choice不会接受第一个参数中的元组列表。

indices = range(0, len(vals))
n = laplace_mech(len(adult), 1, 1.0)
gen_indices = np.random.choice(indices, int(n), p=probs_norm)
syn_data = [vals[i] for i in gen_indices]

syn_df = pd.DataFrame(syn_data, columns=['Age', 'Occupation'])
syn_df.head()

在这里插入图片描述
同时考虑两列的缺点是我们的准确性会更低。当我们向正在考虑的集合中添加更多列时（即，构建一个 $n$ 向边际，增加 $n$ 的值），我们看到与对列联表相同的效果 - 每个计数变小，因此信号相对于噪声变小，并且我们的结果不那么准确。我们可以通过在新的合成数据集中绘制年龄直方图来看到这种效果;请注意，它具有大致正确的形状，但它不如原始数据或我们用于年龄列本身的差异私有计数那么平滑。

plt.xlabel('Age')
plt.ylabel('Number of Occurrences')
plt.hist(syn_df['Age'], bins=bins);

在这里插入图片描述
当我们仅对年龄列尝试特定查询时，我们会看到相同的准确性损失：

real_answer = range_query(adult, 'Age', 20, 30)
syn_answer = range_query(syn_df, 'Age', 20, 30)
print('Percent error using synthetic data:', pct_error(real_answer, syn_answer))