【数据结构与算法】最小生成树-Prim算法(2)

最小生成树-Prim算法(2)

  前文介绍了有关图的基本知识，本文将以无向图和邻接矩阵为例，用Prim算法实现最小生成树。

1. 问题引入

  假设目前有v0，v1…v8一共9个村庄，村庄之间的数字表示两村之间的距离，比如10表示v0和v1两个村庄相隔10km。如果我们要为这9个村庄铺路，要求任意两个村庄都能够连通，并且铺路花费成本最低。如果你是规划的工程师，该怎么进行规划呢？这就是一种很典型的最小生成树问题。

2. 什么是最小生成树

  最小生成树其实包含了三个概念。最小、生成和树

2.1 树

 树的含义就是，如果有n个结点，应该只有n-1条边把这些结点连接到了一起

  比如上图就是树结构，除了根节点A以外，每个结点都有一条输入的线。所以10个结点，总共有9条线。
  这其实也就意味是，n个结点，少于n-1条线的时候无法构成树；多于n-1条线的时候，必然会产生环。

2.2 生成树

  生成树的概念是，对于一个连通图来说，包含这个连通图的全部n个结点；有n-1条线连接这n个结点，并且没有环；生成树中的任意两个结点之间都是连通的。

2.3 最小生成树

  最小生成树就是在生成树的概念上，加入了所有连接线的权值和最小这一约束条件。
  综合一下，最小生成树的约束条件有：（1）必须只使用该图中的边来构造最小生成树；（2）必须使用且仅使用（n-1）条边来连接图中的n个顶点；（3）不能使用产生回路的边；（4）要求树的（n-1）条边的权值之和是最小的。

3. Prim算法实现过程

  Prim算法是一种贪心算法，从某一个结点开始搜索，搜索与这个结点相连的边，选择权值最小的一条边进行连接。于是就有了两个结点，继续搜索与这两个结点相连的全部结点，连接权值最小的边，不断循环，直到所有的结点都被连接起来。
  举例如下^[2]:
  (1)假如有如图a所示的图，要对其进行搜索，产生最小生成树

（2）选定0为起点，搜索与0相连的点，有1,2和3，权值分别是1,5,6其中与结点1的连线权值最小，所以连接0和2

(3)继续搜索与0和2相连接的结点，发现有1,3,4,5。从0和2出发，有6条线可以进行连接，分别是(0-1)6,(0-3)5,(1-2)5,(2-3)5,(2-4)6,(2-5)4，其中2和5之间的连线4是最短的，连接2和5

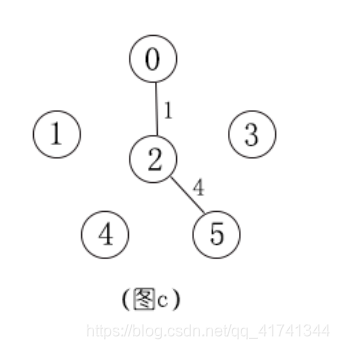
(3)继续搜索0,2,5和其余未连接的点，发现有8条可以连接其余点的线，其中(3-5)2这条线的权值最小。

(4)继续搜索，当所有的点都被连接上的时候，搜索结束，产生最小生成树。

  这就是prim算法的思路，从结点出发进行搜索，不断寻找最优的下一个结点，以完成构成最小生成树。

4. Prim算法代码实现

4.1 构成Prim算法的关键结构

  从上文Prim算法的实现思路上来讲，其实我们储存三个数据

1. 目前哪些点已经被连接上了
2. 目前连接上的点连接外部点的最短线段是谁
3. 已连接的点集与外部点集之间的最短线段权值是几

4.2 Prim算法关键结构定义

  还是以这个图为例，假设我们定义了如下变量

int adjvex[MaxVex]; //用来保存当前已经连接好的树与其余没有连接好的结点间构成最短距离的结点对
int lowcost[MaxVex];  //用来储存当前已经连接好的树与其他没有连接好的结点间的最短距离

4.2.1 int adjvex[MaxVex];

  adjvex是一个边集，i和adjvex[i]表示一条线段，是当前以及连接好的点集与外部点集之间的最短距离

  比如图c，以及连接好的点集0,2,5与外部点集1,3,4,5进行连接
0,2,5构成的点集与1之间能连线的是(0-1)6和(2-1)5，因为(2-1)5更短，所以我们会保存这条边
  其余的点也是类似的。所以，当0,2,5被连接好的时候，与其余点的最短距离数组adjvex应该是

0	1	2	3	4	5
0	2	0	5	5	2

  adj[1] = 2表示，当前点集(0,2,5)与结点1相连，最短的边是（1-2）

4.2.2 int lowcost[MaxVex];

  adjvex其实已经完成了4.1说提到的第两个问题，能够表示当前点集与外部进行连接，最短线段是那条(i-adjvex[i]);
  而lowcost数组记录的，其实就是线段(i-adjvex[i])的权值。当权值被标记为0的时候，意味着这个点已经被连接了(权值0表示自己连接自己)

4.3 Prim算法实现

  Prim算法实现包含了三个步骤

• (1) 加入
    当前点集加入一个新结点(第一次会直接加入结点0)。并在adjvex数组的相应位置标记0
• (2) 更新
    更新新结点与外部结点之间的最短距离，分别更新到adjvex数组和lowcost数组中
• (3) 查找
    从当前记录的lowcost数组中，遍历已连接结点与外部所有结点的最短距离，选择权值最小的那个，作为下一个连接结点。并把lowcost的相应位置标记为0。

4.4 代码实现

&  基于无向图和邻接矩阵进行实现

#include<iostream>
using namespace std;
//--------------------------------邻接矩阵结构------------------------------------------------

typedef int VertexType; //结点类型
typedef int EdgeType;  //边类型
const int MaxVex = 100;  //最大顶点数
const int Infinity = 65535; //表示无穷

typedef struct
{
	VertexType vexs[MaxVex];//定义顶点
	EdgeType arc[MaxVex][MaxVex]; //定义边(弧)
	int numVertexes, numEdges; //当前定义数和边数
}MGraph;



//--------------------------------邻接矩阵结构定义结束-----------------------------------------


//--------------------------------------基于邻接矩形无向图的创建---------------------------------

void CreateGraph(MGraph* g)
{
	//输入个数信息
	cout << "请输入顶点数和边数" << endl;
	cout << "顶点:" << ends;

	cin >> g->numVertexes;
	cout << "边数:" << ends;
	cin >> g->numEdges;

	//输入顶点信息
	cout << "请输入顶点信息:" << endl;
	for (int i = 0; i < g->numVertexes; i++)
	{
		cin >> g->vexs[i];
	}

	//边信息的初始化
	for (int i = 0; i < g->numVertexes; i++)
	{
		for (int j = 0; j < g->numEdges; j++)
		{
			if (i == j)
			{
				g->arc[i][j] = 0;
			}
			else
			{
				g->arc[i][j] = Infinity;
			}
		}
	}

	//建立邻接矩形
	for (int i = 0; i < g->numEdges; i++)
	{
		cout << "请输入边(vi,vj)对应的下标i，j和权w" << endl;
		int row, col, w;
		cin >> row >> col >> w;
		g->arc[row][col] = w;
		g->arc[col][row] = g->arc[row][col]; //因为无向图，所以是对称矩阵

	}







}

//--------------------------------------基于邻接矩形无向图的创建结束-------------------------------

//-----------------------------------------基于邻接矩形和prim算法的最小生成树------------------------

void MiniSpanTree_Prim(MGraph g)
{
	//01 创建需要的变量
	int adjvex[MaxVex]; //用来保存当前已经连接好的树与其余没有连接好的结点间构成最短距离的结点对
	int lowcost[MaxVex];  //用来储存当前已经连接好的树与其他没有连接好的结点间的最短距离

	adjvex[0] = 0; //表示从结点0开始进行搜索
	lowcost[0] = 0;  //lowcost储存的距离分为三种
					//(1)Inf,表示目前adjvex中的相应结点对没有连接关系
	                  //(2)普通数字，lowcost[j]表示adjvex[j]和j之间的距离
					//（3）表示两个结点已经连接上了，j和adjvex[j]两个结点都属于生成树了

	//02 初始化，从结点0开始，先计算结点0和其余各个点之间的距离
	for (int i = 1; i < g.numVertexes; i++)
	{
		adjvex[i] = 0; //构成边集 i和adjvex[i]是一条边的两个结点
	}
	for (int i = 1; i < g.numVertexes; i++) //距离数组初始为结点0和其余各个结点的距离
	{
		lowcost[i] = g.arc[0][i];
	}

	//03 
	int k=0;
	for (int i = 1; i < g.numVertexes; i++)//这个外循环的意义在于，防止图不是联通图，有多个子图，会有多个最小生成树
	{
		int min = Infinity;

		//03-1 搜索结点
		for (int j = 1; j < g.numVertexes; j++)
		{
			if (lowcost[j] != 0 && lowcost[j] < min) //搜索树和外部结点之间的最短距离，并记录那个结点
			{
				min = lowcost[j];
				k = j; //保存距离最小的位置
			}
		}

		//03-2 输出边
		cout << adjvex[k] << "-" << k << endl;
		lowcost[k] = 0; //表示k和adjvex[k]两个结点成功连接

		//03-3 更新边集和距离集合


		//刚刚结点k与生成树完成了连接，搜索结点k与其余各个未连接的结点之间的距离，如果k和j连接的线段比现在存的
		//j和adjvex[j]之间的距离lowcost[j]要短，那么就让adjvex[j]=结点k，并将lowcost[j]更新为k和j之间的距离
		for (int j = 1; j < g.numVertexes; j++)
		{
			if (lowcost[j] != 0 && g.arc[k][j] < lowcost[j])
			{
				adjvex[j] = k;
				lowcost[j] = g.arc[k][j];
				
			}
		}


	}


}

//---------------------------------------基于邻接矩形和prim算法的最小生成树结束---------------------
int main()
{

	MGraph m;
	CreateGraph(&m);
	MiniSpanTree_Prim(m);
	return 0;
}

5.参考资料

【1】大话数据结构
【2】https://blog.csdn.net/aa793336532/article/details/71680311
【3】https://www.bilibili.com/video/BV1Eb41177d1