【现代信号处理】 10 - 自适应应用与LMS变种

自适应应用与LMS变种

1. 自适应应用的基本框架

  如果信号处理中没有自适应的话，我们的框架是这样的。输入一个信号Z，经过滤波器，得到信号Y。

  但是现在的问题是Z是随时变的，Y也是随时变的，一个固定的滤波器没有办法解决问题。因此我们引入了自适应模块。

  引入了自适应模块以后，通过滤波器以后得到的估计就不一定是最优估计了，我们与真实值进行比较，得到了误差e，然后把误差送人自适应滤波器中，得到一个新的系数ω，从而调整滤波器，通过不断的对滤波进行更新，使得最终的误差变小。

  误差大的原因主要来自于两个方面，一方面可能是滤波器还没用调整好，训练时间不够。另一方面是因为数据Z在不断的变动，即使这样，也不代表之前训练的数据没有用，基于前面的数据进行调整，才能够得到更好的结果。

2. 自适应滤波与机器学习

  自适应滤波的思想与机器学习极其的相似。

  比如我们现在产生了一个误差，我们是通过误差去驱动自适应的，这个在机器学习中就是监督学习。监督学习就必须要给标准答案。监督学习的结果与标准答案之间会产生误差，通过误差来驱动学习，就是监督学习。

  如果还没训练好，还在不断的对滤波器进行调整，这个在机器学习中就是训练。

  调整好了，但是我们发现信号变了，我们需要去追踪信号的变化，这个在机器学习中就叫做迁移学习。比如我们做机器学习的时候，先去github先去找找open source的东西，看看有没有现成的model，然后以这个为基础和初值，继续训练，训练它没有训练过的东西，就叫做迁移学习。这就相当于在已经调整好的滤波器的基础上，去跟踪新信号的变化。

$$\begin{gathered} \text{Error-Driver}\Rightarrow \text{ Supervised Learning} \\ \text{Adaptive Adjustment}\Rightarrow \text{ Training} \\ \text{Tracking Variation}\Rightarrow \text{Transfert Learning} \end{gathered}$$

3. 自适应思想的应用

  自适应的根本就是在改变输入和输出的方式。

3.1 预测

  第一种应用，就是预测。

  信号Z_n作为输入，正常输出就是Y，另一边，对信号进行延时，通过构造预测器，产生预测信号\hat Y,与真值进行比较，得到误差，根据这个误差进行自适应，从而调整预测器。

  信号预测最重要的应用是做语音编码。前面讲过线性预测编码，通过莱文森迭代和维纳滤波来实现，但是要求系统必须是平稳的。而使用自适应滤波的方法，就没有平稳性的限制了。

3.2 系统辨识

  有一个等待辨识的系统，输入一个Z，输出是Y。我们构造一个系统的模板，自己实现一个系统，让他去接近与我们需要辨识的系统。可能与需要辨识的系统不一样，但是只要输入输出是一致的就行。

  我们的系统也会输出一个Y，两者进行比较，得到误差e，就可以让我们来自适应了，通过输入和误差，调整我们设计的系统。

  系统辨识的最主要的应用在自适应控制上。如果我们想对系统进行有效的控制，我们首先要做的就是被控制的系统是什么样子的。

  知道了控制系统是什么样子，才能够根据输出推断输入控制量是什么样子的。

3.3 逆滤波

  信号通过一个变化，又引入了一些噪声，通过滤波器，输出一个信号。然后我们试图用滤波以后的信号去恢复原始的信号，利用恢复过程中产生的误差去做自适应，调整滤波器。

  逆滤波是把被污染了、被畸变过的信号作为输入，试图去把这个信号进行恢复。

  逆滤波的应用就是通信。通信在信道发送的过程中，就会发生畸变，我们希望把这种畸变消除掉。这种操作就叫做均衡。

  因为信道很难是平稳不变的，因此一定有自适应的需求。移动通讯中，信道的均衡技术是核心技术。

3.4 干扰消除

  我们有一个信号和噪声的信号，我们又有一个驱动信号。

  我们试图以驱动信号作为起点，构造消除器。

  消除器信号与信号和噪声信号进行比较，得到的误差进行自适应。

  消除器是为了把信号和噪声复现出来。最终的输出会把这个复现的信号减掉，这样的话，其他的信号里面就没有这部分了。

  这个应用就是回声抵消。我们希望能够在电话系统中，复制出回声，然后把它减去。

4. LMS的变种

4.1 从步长角度考虑的变种

4.1.1 步长的重要性

$$\omega (k+1)=\omega (k)+\mu Z(k)e(k)$$

  在自适应滤波器中，我们通过输入和误差构建搜索方向，但是另外一个问题就是，步长怎么选。

  我们在前面其实已经得到了步长的限制条件了，因为我们有收敛的条件，所以要求底数小于1，因此就可以得到

$$0<\mu <\frac{2}{{\lambda }_{max}}$$

  步长的这个限制条件是下式得到的。

$$(1-\mu {\lambda }_k{)}^n$$

  实际上，我们在选择步长的时候，不能太大，大了不满足限制条件。同时也不能太小，太小的话，一方面搜索速度满，另外一方面，有可能陷入局部极小值。

  不收敛的意思有两种，一种是反复震荡，震荡幅度很大，步长太大可能存在这个问题。两个一种不收敛是指不收敛到我们需要的极值，步长小可能会出现这个问题，进入局部极小的坑里，就很难出来。

4.1.2 归一化LMS

4.1.2.1 概述

  实际上，关于自适应滤波器，有些人的观点认为，其步长也应该是自适应的，应该根据输入数据去调整步进值。

  于是就有了这样的式子

$$\omega (k+1)=\omega (k)+\frac{1}{{\sum }_{i=1}^N{Z}_i^2(k)}Z(k)e(k)$$

  这个式子中，我们把步长和输入数据联系到了一起，当输入数据比较长的时候，步子就比较小；当输入数据比较短的时候，步长就比较大。也就相当于实现了步长的自适应。这个LMS叫做归一化的LMS。

$$\omega (k+1)=\omega (k)+\frac{Z(k)}{{\sum }_{i=1}^N{Z}_i^2(k)}e(k)$$

4.1.2.2 感性理解

  我们先从感性上来理解这个式子在做什么。我们知道，误差e其实是个标量，也就是说，优化的方向只与Z有关，我们希望Z代表优化方向，e代表优化大小。因此，我们有理由要求Z是一个归一化的方向向量，我们不希望Z是个有大小的向量。本来我们的愿望是，希望步长也是个自适应的，但是我们有更好的选择，我们直接让Z除以他的模做归一化就好了。

4.1.2.3 公式证明

  我们再来从数据公式上对归一化的LMS进行证明。因为我们对步长有这样的要求，首先希望他尽可能小，不然会不收敛；然后，我们也希望步长不能太小，否则就会原地踏步。

  为了使得步子足够小，我们有这样的目标函数

$$\begin{gathered} \omega (k)\Rightarrow \omega (k+1) \\ min(\omega (k+1)-\omega (k){)}^2 \end{gathered}$$

  为了不固步自封，我们增加一个约束条件

$$\begin{gathered} min(\omega (k+1)-\omega (k){)}^2 \\ s.t.\omega (k+1{)}^{T}Z(k)=d(k) \end{gathered}$$

  这个约束条件的意思是这样的。我们计算出来一个新的权重，但是新的数据还没到来，我们就要求这个新计算得到的权，能够对老数据进行线性组合，得到对目标的估计。也就是要求新产生的方向，能够在当前数据和目标的基础上得到满足。

  我们来计算条件极值，在约束条件下，极小化均方误差。因为我们希望得到的结果是个+号项，所以这里求条件极值的时候写了个-λ。

$$\begin{gathered} L(\omega (k+1),\lambda )=||\omega (k+1)-\omega (k)|{|}^2-\lambda (\omega (k+1{)}^{T}Z(k)-d(k)) \\ ={\omega }^T(k+1)\ast \omega (k+1)-2\ast {\omega }^T(k+1)\ast \omega (k)+{\omega }^T(k)\ast \omega (k)-\lambda (\omega (k+1{)}^{T}Z(k)-d(k)) \end{gathered}$$

  求导

$$\begin{gathered} {\nabla }_{{\omega }_{k+1}}L=2\ast \omega (k+1)-2\ast \omega (k)-\lambda Z(k)=0 \\ \omega (k+1)=\omega (k)+\frac{\lambda }{2}Z(k) \end{gathered}$$

  接下来我们需要解决λ的问题了，我们需要用到我们的约束条件

$$\begin{gathered} \omega (k+1)\ast Z(k)=d(k)\Rightarrow (\omega (k)+\frac{\lambda }{2}Z(k){)}^T\ast Z(k)=d(k) \\ {\omega }^T(k)Z(k)+\frac{\lambda }{2}{Z}^T(k)\ast Z(k)=d(k) \\ \frac{\lambda }{2}=\frac{d(k)-{\omega }^T(k)Z(k)}{||Z(k)|{|}^2}=\frac{e(k)}{||Z(k)|{|}^2} \end{gathered}$$

  我们发现得到的式子上面部分就是误差。

  因此

$$\omega (k+1)=\omega (k)+\frac{\lambda }{2}Z(k)=\omega (k)+\frac{e(k)}{||Z(k)|{|}^2}\ast Z(k)$$

  所以，在感性认识的基础上，我们得到了数学公式的证明。

4.1.3 线性平滑LMS

  关于使用自适应的步长，我们还可以有其他的理解。

  其实我们觉得，我们对自适应步长的看法，还应该考虑其他问题。LMS的搜索方向是由新输入的数据决定的，但是很多时候，我们觉得，只调整Z的长度是不太够的，还应该调整Z的方向。按理来说，Z的方向就是梯度，还能怎么调整呢?但是，如果仔细考虑，如果输入数据Z是个野数据，那么优化的方向就完全跑偏了，这个似乎并不太安全。因此，我们有这样的式子。

  本来的迭代方程是这个样子的

$$\omega (k+1)=\omega (k)+g(k)g(k)=\mu Z(k)e(k)$$

  我们用这样子的思路来进行优化

$$\begin{gathered} \omega (k+1)=\omega (k)+g(k)g(k)=\mu Z(k)e(k) \\ g(k)=h(g(k-1),...,g(k-n),Z(k)e(k)) \end{gathered}$$

  也就是说，我们在进行迭代的时候，优化方向不仅仅考虑最新的数据的梯度，而是把前面已经发生的事情全都考虑一下。

  比如我们可以设立一个窗口，对窗口内的数据全部都取平均

$$\begin{gathered} g(k)=h(g(k-1),...,g(k-n),Z(k)e(k)) \\ =\frac{1}{n}\sum _{i=1}^{n}Z(k-i)e(k-i)+Z(k)e(k) \end{gathered}$$

  这么做的好处和坏处都非常的明显。

  好处是，万一得到的新数据是一个野数据，就有很好的容灾能力，因为前面已经形成了一个比较好的搜索方向，即使后面来了一个坏数据，也能得到修正。

  但是坏处是，我们搜索的速度会减慢，因为我们背负了历史的负担。

  更好的方法是，我们增加一个权重。
$$\begin{gathered} g(k)=h(g(k-1),...,g(k-n),Z(k)e(k)) \\ =\sum _{i=1}^n{\lambda }_{i}Z(k-i)e(k-i)+Z(k)e(k) \end{gathered}$$

  我们希望权重能够反映出时间的重要性，也就是越新的数据权重越高，我们可以让λ是一个0-1的数字，然后引入指数，这样就能够做到越久远的数据对系统影响越小。这个λ称为遗忘因子。
$$\begin{gathered} \omega (k+1)=\omega (k)+g(k) \\ g(k)=\sum _{i=1}^n{\lambda }^{i}Z(k-i)e(k-i)+Z(k)e(k)(i) \\ \lambda \in (0,1),\text{ Forgotten Factor} \end{gathered}$$

  类似式(i)的这种滤波器就叫做线性平滑滤波器

$$\text{Linear Smothing LMS}$$

4.1.4 非线性平滑LMS

  但是，线性平滑滤波器是否惧怕冲激噪声(或者说是重拖尾现象)。含有冲激噪声的数据做线性平滑LMS，可能效果很不好。我们可以类比最小二乘，最小二乘就十分害怕冲激噪声，为了抵消一个冲激噪声的影响，最小二乘曲线会发生很大的偏移

• 没有拖尾线性的最小二乘

• 有拖尾的最小二乘

  为了能够抵消冲激噪声，我们就不能用均值滤波的思路了，我们就要使用中值滤波的思路。中值滤波在图像处理中使用的很多，因为图像中会经常出现亮点。

  对矢量取中值，就是每一个分量都取中值。中值滤波的好处是稳健性强，但是缺点是效率很低。

$$\begin{gathered} \text{Impulse Noise}\Rightarrow \text{Heavy-Tailed Noise} \\ \omega (k+1)=\omega (k)+g(k) \\ g(k)=median(Z(k)e(k),Z(k-1)e(k-1),....,Z(k-n)e(k-n)) \end{gathered}$$

  中值滤波用到了排序算法。排序算法中最有效的就是快速排序。时间复杂度是O(nlogn)。

  中值滤波就是一种非线性平滑LMS

$$\text{Nonlinear Smothing LMS}$$

4.2 从效率角度考虑的变种

4.2.1 考量效率的必要性

  如果我们考虑的是效率至上的时候，LMS又可以进行变形。最关键的思想就是，尽可能不做乘法运算。这是因为乘法运算是件非常麻烦的事情。举个例子，在8086中，加法是4个时钟周期，乘法是65个时钟周期。这还不是浮点数乘法。在286中加入了协处理器，乘法加法就在一个时钟周期内就完成了。

  因此，如果效率至上的时候，我们可以不做乘法。就比如fft，本质就是ab+ac = a(b+c)，乘法能少做就少做。

  避免乘法运算的方法就是使用符号函数。符号在电路里就是极性，实现非常简单，因此可以代替一次乘法

4.2.2 sign LMS

  符号LMS是这么定义的

$$\omega (k+1)=\omega (k)+\mu Z(k)e(k)\Rightarrow \omega (k+1)=\omega (k)+\mu Z(k)sgn(e(k))$$

  这么做也是非常有意义的。比如，如果我们想把算法放到移动终端去，复杂度、重量、成本、体积、功耗就全部都非常重要了，能搞的多小，就搞多小。

4.2.3 double sign LMS

  比sign LMS更加节省计算时间的还有double sign LMS

$$\omega (k+1)=\omega (k)+\mu Z(k)e(k)\Rightarrow \omega (k+1)=\omega (k)+\mu sgn(Z(k))sgn(e(k))$$

4.3 小结–LMS、学习与机器学习

4.3.1 LMS与学习

  我们再回过来看这个g(k)

$$g(k)=\mu Z(k)e(k)$$

  我们这里来对LMS的变种做一个更加形象的对比。

  比如说我们的考试，如果我们考试成绩不好，可能有两个原因。一个原因是考试没有复习好，另外一个原因是题目出的太偏了。

  这个放到LMS中就是，如果我们得到的e(k)太大了，说明我们没有复习好，我们就要用更大的步长去努力学习。

  而如果是Z(k)太大了，这可能是一个冲激，也就是考试题目太偏了，这个时候我们不会放弃考试的主要考纲，而把中心放到偏题，怪题上。因此，我们会选择对Z(k)做校正。

  如果我们使用归一化的方法对Z(k)做校正，就是研究研究考试中比较常规的题目，偏题就不看了。如果我们使用线性平滑的方法，就是说把最近的考试试卷全部都拿出来看看，比较类似的题目就好好研究，每次考试中不同的东西就考虑考虑，到底需不需要加强这个知识点。

4.3.2 学习与机器学习

  其实我们现在的机器学习发展遇到了瓶颈，很大的一个原因是，没有好好研究人的学习过程。比如人学习的时候，老师总会给予一些提升，但是机器学习就没有这种思想。

  机器学习只会做误差的反向传播。比如我们考试的时候，题目答案是2，而我们计算了个20000，正常人第一反应都是，从第一步去看看，是不是题意理解错了。而机器学习是，先从最后一步看起，把2和20000做差，得到19998，进行反向传播，修正误差。然后再看倒数第二步，倒数第三步等等。人是不会这么学习的，这么学习学不到知识。反向传播轮数多了以后就没有信息量了。所以，机器学习的方法，就不是人学习的思路。没有办法得到有效的引导，非常机械的反向传播，学习效果就不是非常好。

  如果能从人学习的角度研究机器学习，可能会更好，就是综合前面的考试结果，综合分析。LMS的各种变种，其实都能够追溯到人的学习。

5. 机器学习与梯度优化

5.1 leaky LMS与冲量梯度下降

5.1.1 Leaky LMS

  Leaky LMS实际上是做一个凸组合

$$\begin{gathered} \omega (k+1)=\lambda \omega (k)+(1-\lambda )g(k) \\ \lambda \in (0,1) \end{gathered}$$

  我们在当前数值和前进的方向之间做一个折中，得到新的值。

  这是因为，我们知道选择比努力重要，方向比能力重要。也就是说，我们不管做什么，起点在哪很重要。如果起点就错了，可能努力多了也没有价值。

  为了防止起点出错，我们的方法就是不要对起点非常信任，我们用权重调整对起点的信任度和对方向的期望。起点和方向其实都有可能是错的，最好的方法就是不要相信任何人，我们就用一个凸组合，去调整信任度。

5.1.2 冲量梯度下降

  Leaky LMS的想法本身是非常朴素的，但是它提出了一个非常重要的思想，在梯度优化里面，leaky思想起到了非常关键的作用。人们因此引入了一个概念，momentum(动量，冲量)

  冲量梯度下降是怎么做的呢?实际上，冲量梯度下降认为，除了权重需要迭代以外，梯度也是需要迭代的。根据物理学定律，任何运动都是具有惯性的，冲量梯度下降相当于对惯性方向和新的梯度方向之间，做了个线性组合，然后得到新的前进方向。

$$\begin{gathered} \{\begin{array}{l}\omega (k+1)=\omega (k)+g(k)\\ g(k+1)=\lambda g(k)+(1-\lambda )\nabla J(Z(k+1))(0)\end{array} \\ \lambda \in (0,1) \end{gathered}$$
  冲量梯度下降得到的这个式子，与leaky LMS是非常相似的。不过一个是在权重上做，一个是在梯度上做。

  实际上，这里的梯度迭代可以看做是一个无限冲激响应滤波器(IIR),因为这个迭代会把全部的历史因素包含进来。不过因为有遗忘因子λ的影响，越老的数据，产生的权重影响越小，越新的数据，产生的权重影响越大。

  我们想把这个结果写的更清楚些，我们下面进行一些数学推导。

$$\{\begin{array}{l}\omega (k+1)=\omega (k)+g(k)\\ \omega (k)=\omega (k-1)+g(k-1)\end{array}$$
$$\Rightarrow \{\begin{array}{l}\omega (k+1)=\omega (k)+g(k)(1)\\ \lambda \omega (k)=\lambda \omega (k-1)+\lambda g(k-1)(2)\end{array}$$

  (1)-(2)可得

$$\begin{gathered} \omega (k+1)-\lambda \omega (k)=\omega (k)-\lambda \omega (k-1)+g(k)-\lambda g(k-1) \\ \Rightarrow \omega (k+1)=\omega (k)+\lambda (\omega (k)-\omega (k-1))+g(k)-\lambda g(k-1) \end{gathered}$$
  代入(0)

$$\omega (k+1)=\omega (k)+\lambda (\omega (k)-\omega (k-1))+(1-\lambda )\nabla J(Z(k))$$

  与正常的梯度下降相比，其实我们就是多了一项动量项,然后最后一个梯度项有所不同

$$\lambda (\omega (k)-\omega (k-1))\text{ Momentum}$$

  动量梯度下降实际上就是，新的方向是旧的方向与新的点的梯度的一个线性组合。ω(k)点的梯度方向与曲面的切线是垂直的。

  正则化和动量项对于神经网络来说都是必须要加的。

5.2 冲量梯度下降存在的缺点

  动量梯度下降后来被人证明，加了这个动量以后，可能会收敛不了，因为产生了一个著名的震荡。也就是有一个非常良好的凸函数，使用动量梯度下降，走几步以后就陷入了死循环

  因此人们认为，对于良性的凸函数都会有震荡，复杂的情况肯定也不好用，因此这种方法就跌落神坛。

5.3 内斯特洛夫加速冲量Nesterov Accelerating momentum

  后来有人对动量梯度下降做了调整，把这个震荡搞没了。

 这个调整的关键就是，使用的梯度不是冲量的起点，而是冲量的终点。

$$\omega (k+1)=\omega (k)+\lambda (\omega (k)-\omega (k-1))+(1-\lambda )\nabla J(Z(k)+\mu (Z(k)-Z(k-1))$$

  新得到的优化就叫做内斯特罗夫加速冲量Nesterov Accelerating momentum

  内斯特罗夫（凸优化优化最有名的人）的工作极其深刻。这里对工作是极其深刻的做一个定义，有三点要求

• 陈述是简单的
• 结果是直观的
• 论证是困难的

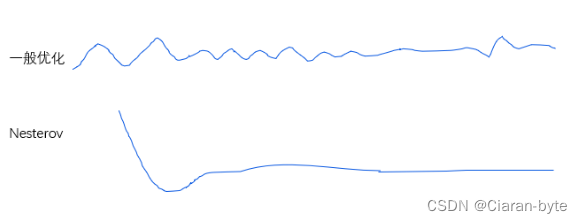
  内斯特罗夫论证是这么冲为什么是最好的。他发明了很多原创的概念。内斯特罗夫加速关键在于梯度的选取上。如果没有用内斯特罗夫，基本优化是震荡前行。用了内斯特罗夫以后，优化就变得平稳了

5.4 其他梯度优化方法

5.4.1 AdaGrad

  针对梯度的优化就有很多方法，比如 AdaGrad

$${\omega }_i(k+1)={\omega }_i(k)+\frac{1}{{\sum }_n{\omega }_i^2(k-n)}\nabla J_i$$
  这个机器学习中很常见，实际上就是把各个参数分开来看。这里面归一化使用是过去的若干时刻同一个位置的分量的大小来进行归一化。

  含义是，现在有很多个参数了，各个参数的调整各不相同，要是在过去几次迭代中，这个东西没怎么动，就给他调的大一点，要是过去几次迭代这个参数动的很厉害，就少调一点。

  这个方法是为了防止出现过拟合或者局部极小。但是实际使用是喜忧参半。因为如果参数不动，说明他可能不重要，也没有必要调整。而如果经常变动，说明他很重要，也没有必要压制他

5.4.2 Adam

  用adam，处处留缝。权值调整的时候留缝，具体调整的方向上，也要留缝。我们在权值和方向上都在兼顾历史与未来。这种方法比冲量走的更远，相当于把leaky LMS和动量梯度下降结合在了一起。

$$\Rightarrow \{\begin{array}{l}\omega (k+1)=\lambda \omega (k)+(1-\lambda )g(k)\\ g(k+1)=\mu g(k)+(1-\mu )\nabla J(Z(k+1))\end{array}$$

6. 结语

  我们如果要做信号处理，我们完全可以让系数自适应化，机器学习化，深度学习化。这里学到的基本思想去处理，应该能够做出比较容易去发表的工作。

  我们这节课介绍的方法有很多，好用才是好方法。