目录
前言
整周模糊度的求解是GNSS高精度定位中的关键性问题,正确快速地固定整周模糊度能使GNSS的定位精度到达厘米甚至毫米级。在GNSS相对定位过程中,通过卡尔曼滤波可以求解得双差整周模糊度参数的浮点解(即小数解)及其方差-协方差矩阵,而由于整周模糊度具有整数特性,那么不管是单差整周模糊度还是双差整周模糊度都理应是整数。如何利用整周模糊度参数的浮点解及其方差-协方差矩阵,正确求得整周模糊度参数的固定解(即整数解),就是模糊度固定要解决的问题(这实际上是一个数学问题)。
本篇整理了LAMBDA算法的理论及其在RTKLIB中的代码部分,由于LAMBDA算法在模糊度固定领域已经非常成熟,博主以往都将其黑箱处理,最近才开始深入学习,若博客中有描述有误的地方,烦请大佬指正,感激不尽!
参考文献:
[1] 李征航, 黄劲松. GPS测量与数据处理.第3版[M]. 武汉大学出版社, 2016.
[2] Jonge P D , Tiberius C . The LAMBDA method for integer ambiguity estimation: implementation aspects[J]. No of Lgr Series, 1998.
[3] Chang X W , Yang X , Zhou T . MLAMBDA: a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy, 2005, 79(9):552-565.
一、LAMBDA算法理论
最小二乘模糊度降相关平差法(Leastsquare AMBiguity Decorrelation Adjustment-LAMBDA)理论严密,搜索速度快,是一种被广泛采用的模糊度固定方法。该方法主要由两部分组成:(1)为降低模糊度参数之间相关性而进行的多维整数变换;(2)在转换后的空间内进行模糊度搜索,然后再将结果转换回模糊度空间中,进而求得模糊度整数解。
1、模糊度参数降相关
由于模糊度之间具有相关性,一个模糊度参数的变化会影响其他模糊度的搜索,使得搜索算法的计算量巨大。如果能够设法降低模糊度参数之间的相关性,使得某一模糊度的变化对其他模糊度的取值的影响尽可能小,就能大大加快模糊度的搜索过程。
LAMBDA算法通过对模糊度参数及其方差-协方差阵进行整数高斯变换(也称z变换),将他们从原空间变换到新的空间中去,实现模糊度的降相关:





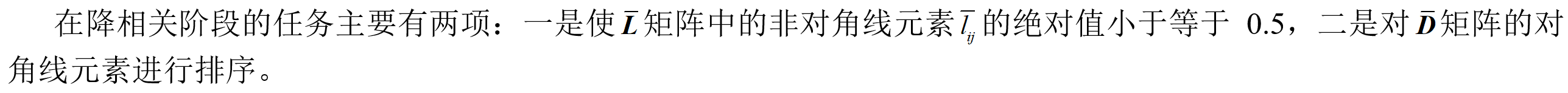
1)使L矩阵中非对角线元素绝对值小于0.5








2)使D矩阵中对角线元素降序排序





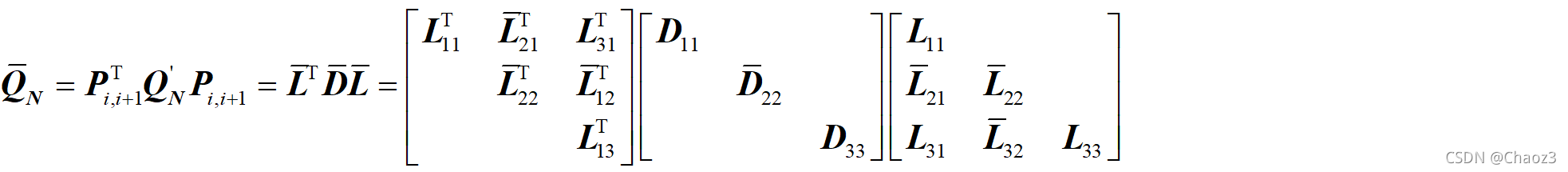


在实际计算中,通常从第n-1列的第一个非对角线元素(即第n行第n-1列的元素)开始,从上往下(第k行到第n行,k表示第一个非对角线元素),从右往左(第n-1列到第1列),交替进行降相关及调序操作,最终的整数变换矩阵即为所有降相关子矩阵Z及调序变换子矩阵P的乘积。
2、模糊度搜索
模糊度搜索与前述的降相关是LAMBDA算法的两个独立的部分,就算不做降相关操作,依然可以进行模糊度搜索,整数模糊度搜索条件(目标函数f):



代入目标函数得:
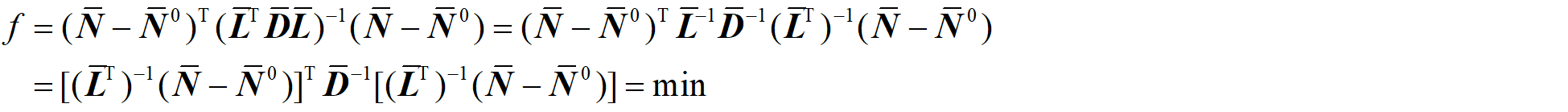






目标函数变为:

其中:








二、RTKLIB中的lambda()函数
RTKLIB中使用的LAMBDA算法,与第一节中所述的LAMBDA算法有些区别,但他们的核心思想是相同的,配合源码学习可帮助理解LAMBDA算法(对代码关键部分进行了注释)。
需要注意的是,RTKLIB中采用lambda算法降相关,mlambda算法搜索。
/* lambda/mlambda integer least-square estimation ------------------------------
* integer least-square estimation. reduction is performed by lambda,
* and search by mlambda. 用lambda算法降相关,mlambda算法搜索
* args : int n I number of float parameters
* int m I number of fixed solutions
* double *a I float parameters (n x 1)
* double *Q I covariance matrix of float parameters (n x n)
* double *F O fixed solutions (n x m)
* double *s O sum of squared residulas of fixed solutions (1 x m)
* return : status (0:ok,other:error)
* notes : matrix stored by column-major order (fortran convension)
*-----------------------------------------------------------------------------*/
extern int lambda(int n, int m, const double *a, const double *Q, double *F,
double *s)
{
int info;
double *L,*D,*Z,*z,*E;
if (n<=0||m<=0) return -1;
L=zeros(n,n); D=mat(n,1); Z=eye(n); z=mat(n,1); E=mat(n,m);
/* LD factorization 对双差模糊度方差-协方差阵Q进行LDLT分解 */
if (!(info=LD(n,Q,L,D))) {
/* lambda reduction lambda降相关 */
reduction(n,L,D,Z);
matmul("TN",n,1,n,1.0,Z,a,0.0,z); /* z=Z'*a */
/* mlambda search mlambda搜索 */
if (!(info=search(n,m,L,D,z,E,s))) {
/* 将在新空间中固定的模糊度逆变换回双差模糊度空间中 */
info=solve("T",Z,E,n,m,F); /* F=Z'\E */
}
}
free(L); free(D); free(Z); free(z); free(E);
return info;
}
降相关子函数reduction()
/* lambda reduction (z=Z'*a, Qz=Z'*Q*Z=L'*diag(D)*L) (ref.[1]) ---------------*/
static void reduction(int n, double *L, double *D, double *Z)
{
int i,j,k;
double del;
j=n-2; k=n-2;
//这里的调序变换类似插入排序的思路?
while (j>=0) {
//由于第k+1,k+2,...,n-2列都进行过降相关并且没有被上一次调序变换影响,
//因此只需对第0,1,...,k-1,k列进行降相关
if (j<=k) for (i=j+1;i<n;i++) gauss(n,L,Z,i,j);//从最后一列开始,各列非对角线元素从上往下依次降相关
del=D[j]+L[j+1+j*n]*L[j+1+j*n]*D[j+1];
if (del+1E-6<D[j+1]) { /* 检验条件,若不满足检验条件则开始进行调序变换 compared considering numerical error */
perm(n,L,D,j,del,Z);//调序变换
k=j; j=n-2;//完成调序变换后重新从最后一列开始进行降相关及排序,k记录最后一次进行过调序变换的列序号
}
else j--;
}
}
搜索子函数search()
搜索的目标函数为:

r的取值决定了超椭圆搜索区域的大小,若r取小了,最优解落在搜索区域外,无法搜索到最优解;若r取大了,搜索区域过大,搜索效率变低。LAMBDA算法里通过某种方式确定r的取值,后续的所有搜索都在固定半径的超椭圆区域中进行,这种固定半径搜索方式的效率依赖于r取值的合理性。
X.W.Chang等提出MLAMBDA算法,此方法在搜索的过程中不断地缩小搜索区域的半径r,大多数情况下的搜索效率都要高于LAMBDA的搜索方式。其原理如下:
由理论部分,对于任一模糊度有:




其伪代码(参考文献3)及代码(RTKLIB)如下:

static int search(int n, int m, const double *L, const double *D,
const double *zs, double *zn, double *s)
{
int i,j,k,c,nn=0,imax=0;
double newdist,maxdist=1E99,y;//maxdist,当前超椭圆半径
double *S=zeros(n,n),*dist=mat(n,1),*zb=mat(n,1),*z=mat(n,1),*step=mat(n,1);
k=n-1; dist[k]=0.0; //k表示当前层,从最后一层(n-1)开始计算
zb[k]=zs[k];//即zn
z[k]=ROUND(zb[k]); y=zb[k]-z[k]; step[k]=SGN(y); //四舍五入取整;取整后的数与未取整的数作差;step记录z[k]是四舍还是五入
for (c=0;c<LOOPMAX;c++) {
newdist=dist[k]+y*y/D[k];
if (newdist<maxdist) { //如果当前累积目标函数计算值小于当前超椭圆半径
if (k!=0) { //情况1:若还未计算至第一层,继续计算累积目标函数值
dist[--k]=newdist; //记录下当前层的累积目标函数值,dist[k]表示了第k,k+1,...,n-1层的目标函数计算和
for (i=0;i<=k;i++)
S[k+i*n]=S[k+1+i*n]+(z[k+1]-zb[k+1])*L[k+1+i*n];//
zb[k]=zs[k]+S[k+k*n]; //计算Zk,即第k个整数模糊度参数的备选组的中心
z[k]=ROUND(zb[k]); y=zb[k]-z[k]; step[k]=SGN(y); //四舍五入取整;取整后的数与未取整的数作差;记录是四舍还是五入
}
else { //情况2:若已经计算至第一层,意味着所有层的累积目标函数值计算完毕
//nn为当前候选解数,m为我们需要的固定解数,这里为2,表示需要一个最优解及一个次优解
//s记录候选解的目标函数值,imax记录之前候选解中的最大目标函数值的坐标
if (nn<m) { //若候选解数还没满
if (nn==0||newdist>s[imax]) imax=nn;//若当前解的目标函数值比之前最大的目标函数值都大,那么更新imax使s[imax]指向当前解中具有的最大目标函数值
for (i=0;i<n;i++) zn[i+nn*n]=z[i];//zn存放所有候选解
s[nn++]=newdist;//s记录当前目标函数值newdist,并加加当前候选解数nn
}
else { //若候选解数已满(即当前zn中已经存了2个候选解)
if (newdist<s[imax]) { //若 当前解的目标函数值 比 s中的最大目标函数值 小
for (i=0;i<n;i++) zn[i+imax*n]=z[i]; //用当前解替换zn中具有较大目标函数值的解
s[imax]=newdist; //用当前解的目标函数值替换s中的最大目标函数值
for (i=imax=0;i<m;i++) if (s[imax]<s[i]) imax=i; //更新imax保证imax始终指向s中的最大目标函数值
}
maxdist=s[imax]; //用当前最大的目标函数值更新超椭圆半径
}
z[0]+=step[0]; y=zb[0]-z[0]; step[0]=-step[0]-SGN(step[0]); //在第一层,取下一个有效的整数模糊度参数进行计算(若zb为5.3,则z取值顺序为5,6,4,7,...)
}
}
else { //情况3:如果当前累积目标函数计算值大于当前超椭圆半径
if (k==n-1) break; //如果当前层为第n-1层,意味着后续目标函数各项的计算都会超出超椭圆半径,因此终止搜索
else { //若当前层不是第n-1层
k++; //退后一层,即从第k层退到第k+1层
z[k]+=step[k]; y=zb[k]-z[k]; step[k]=-step[k]-SGN(step[k]); //计算退后一层后,当前层的下一个有效备选解
}
}
}
// 对s中的目标函数值及zn中的候选解进行排序(以s中目标函数值为排序标准,进行升序排序)
// RTKLIB中最终可以得到一个最优解一个次优解,存在zn中,两解对应的目标函数值,存在s中
for (i=0;i<m-1;i++) { /* sort by s */
for (j=i+1;j<m;j++) {
if (s[i]<s[j]) continue;
SWAP(s[i],s[j]);
for (k=0;k<n;k++) SWAP(zn[k+i*n],zn[k+j*n]);
}
}
free(S); free(dist); free(zb); free(z); free(step);
if (c>=LOOPMAX) {
fprintf(stderr,"%s : search loop count overflow\n",__FILE__);
return -1;
}
return 0;
}
























 682
682

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








