GNSS伪距及载波相位观测模型

前言

最小二乘与卡尔曼滤波是目前GNSS定位中主流的二类平差滤波方法，而构建观测模型是此二类方法的关键步骤。本篇从伪距和载波相位观测方程出发，推导了伪距单点定位，RTK相对定位，历元间三差相对定位中的观测模型。主要参考RTKLIB、《GPS测量与数据处理》及《GPS原理与接收机设计》书籍。

一、观测方程

1、伪距、载波相位观测方程

其中，p为伪距观测值(单位m)，r为真实卫地距(单位m)，c为光速(单位m/s)，光速乘的那部分为接收机钟差及卫星钟差(单位s)，I为电离层延迟(单位m)，T为对流层延迟(单位m),φ为载波相位观测值(单位rad)，λ为载波波长(单位m),N为整周模糊度(单位rad)。伪距观测及载波相位观测中都在方程尾引入了测量噪声项，代表了所有未直接体现在方程中的误差总和，为了方便公式书写，后续将其忽略。

2、单差、双差、三差观测方程

单差观测：
伪距观测及载波相位观测在流动站与基准站之间求一次差，可以消除卫星钟差，在短基线情况下（基站流动站之间的距离不超过10km），可以消去电离层和对流层延迟误差，忽略测量噪声项，得到如下观测方程：

双差观测：
单差观测在同系统卫星p与卫星q之间作二次差，可消去接收机钟差，得到双差观测方程：

三差观测：
双差观测在此历元与上一历元之间作三次差，可消去双差整周模糊度参数（常量），得到三差观测方程：

二、观测模型

1、伪距单点定位（SPP）最小二乘观测模型

伪距观测方程中的r为真实的卫地距，由于真实接收机位置未知，真实卫地距是无法计算的，我们只能给定一个大致的接收机位置[x, y, z]（ECEF_xyz坐标系下，后续默认都在此坐标系下），可求得卫星与接收机大致位置之间卫地距ρ：

真实卫地距r:

在真实位置处泰勒展开并取一阶项，可得：

则伪距观测方程可写为：

通过上式我们可以构建最小二乘的几个矩阵：

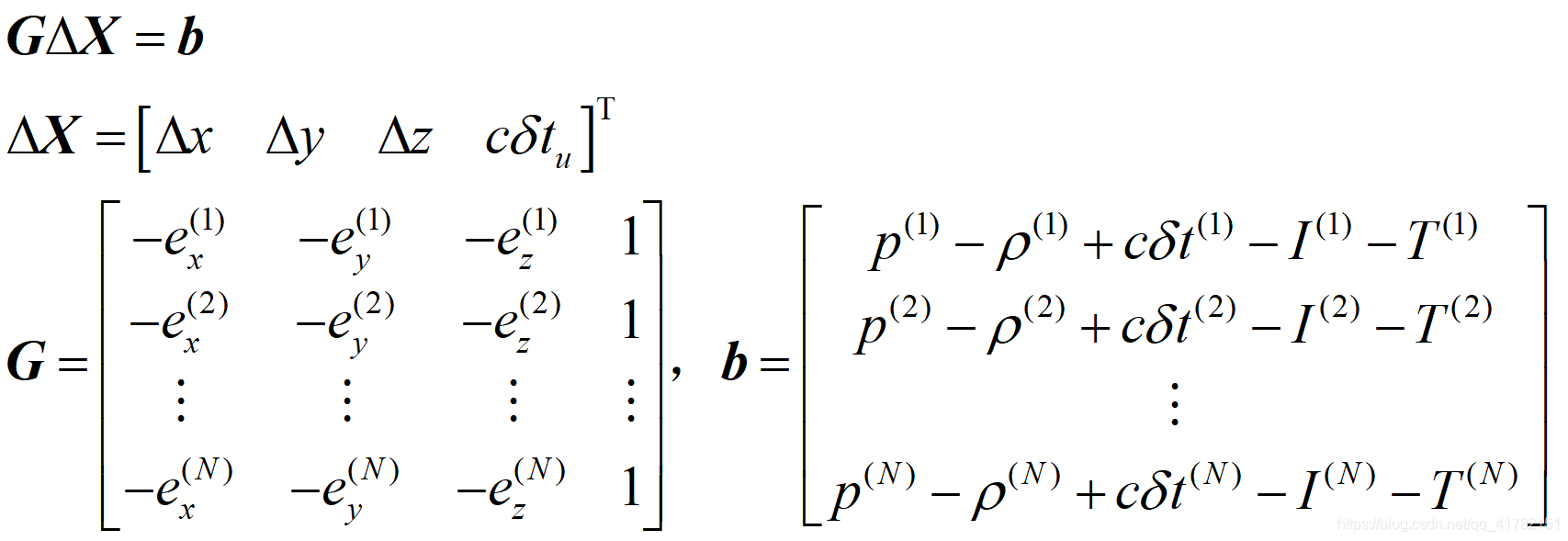
然后通过最小二乘求解公式完成一次位置的迭代更新：

上式中的P为伪距观测的权值矩阵，一般通过卫星高度角定权模型给出，迭代计算10次以下（RTKLIB）就可收敛得到伪距单点定位结果。

2、载波相位相对定位（RTK）卡尔曼滤波浮点解量测模型

浮点解求解使用伪距及载波相位双差观测，双差观测方程：

上式的r为真实双差卫地距，用下标i表示流动站，j表示基站（基站由于真实坐标已知，认为真实卫地距已知），上标p表示卫星p，q表示卫星q，代入真实卫地距线性化结果并站间作差星间作差可得：

上式代入双差观测方程：

通过上式我们可以构造卡尔曼滤波量测模型，根据状态参数的不同，主要有以下两种构造方式：

（1）以单差模糊度参数作为状态量（RTKLIB）

根据状态量的不同对双差观测方程进行适当的变换：

根据上式，可以构建卡尔曼滤波浮点解求解的量测模型（假设观测到N颗卫星，以第一颗卫星作为双差基准星）：

V(t)为双差观测量的误差，一般是通过伪距误差（事先设定的定值）及载波相位误差（事先设定的定值）通过双差变化得到。

（2）以双差模糊度误差作为状态量

将双差模糊度的误差（整数）分离出来，得到观测方程：

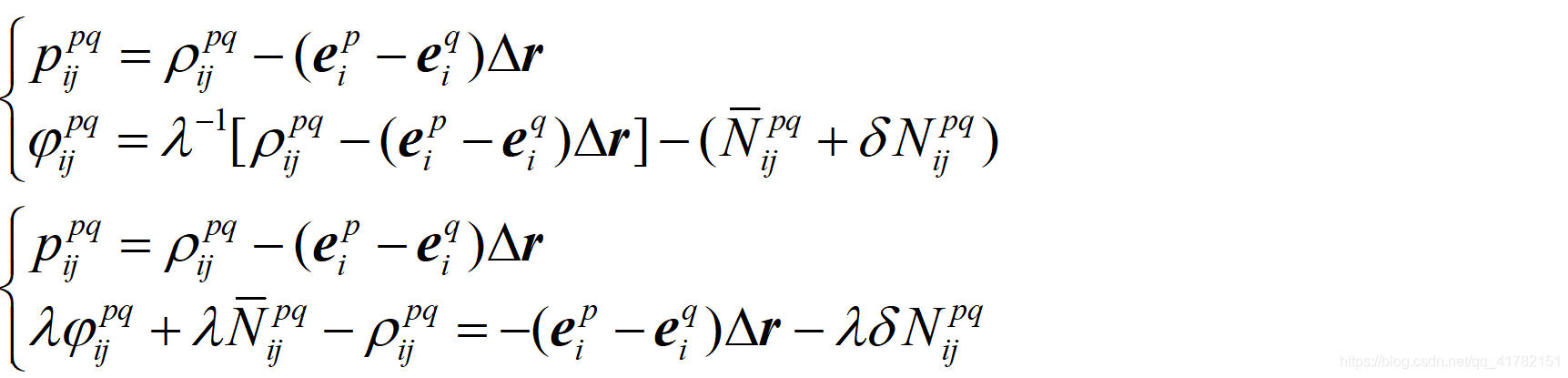
带-上标的N表示为上一历元双差模糊度的最优估计，根据上式，构建卡尔曼滤波浮点解求解的量测方程（假设观测到N颗卫星，以第一颗卫星作为双差基准星）：

然后通过卡尔曼滤波量测更新公式完成卡尔曼滤波浮点解的求解。

3、 历元间三差最小二乘观测模型

三差观测方程：

对于三差卫地距，在历元间作了一次差，我们认为上一历元的位置结果是精确的（即t1历元的双差卫地距是精确已知的），以t2历元的伪距单点定位位置解作为此历元接收机大致位置，代入t2历元双差卫地距的线性化结果，此时的真实三差卫地距写为：

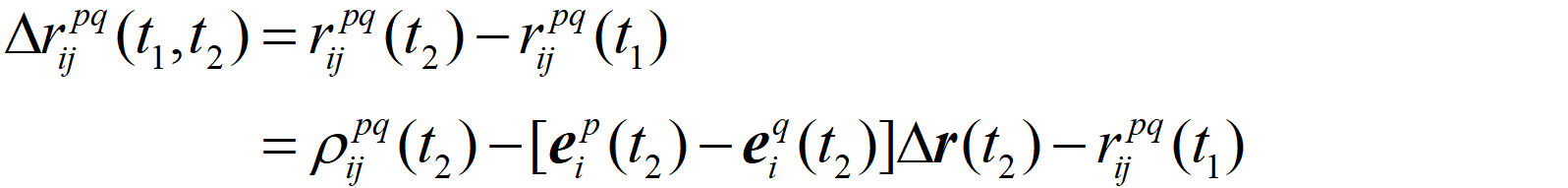
上式中的delta_r(t2)表示t2历元的真实位置与t2历元大致位置间的误差。将上式代入三差观测方程，可得:

移项得：

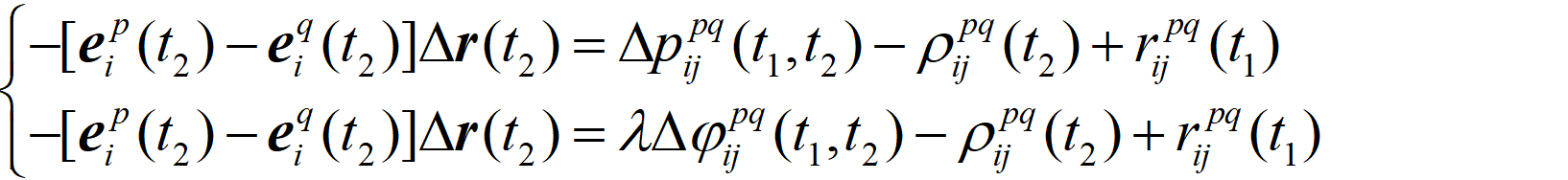
通过上式我们可以构建出最小二乘的各项矩阵：

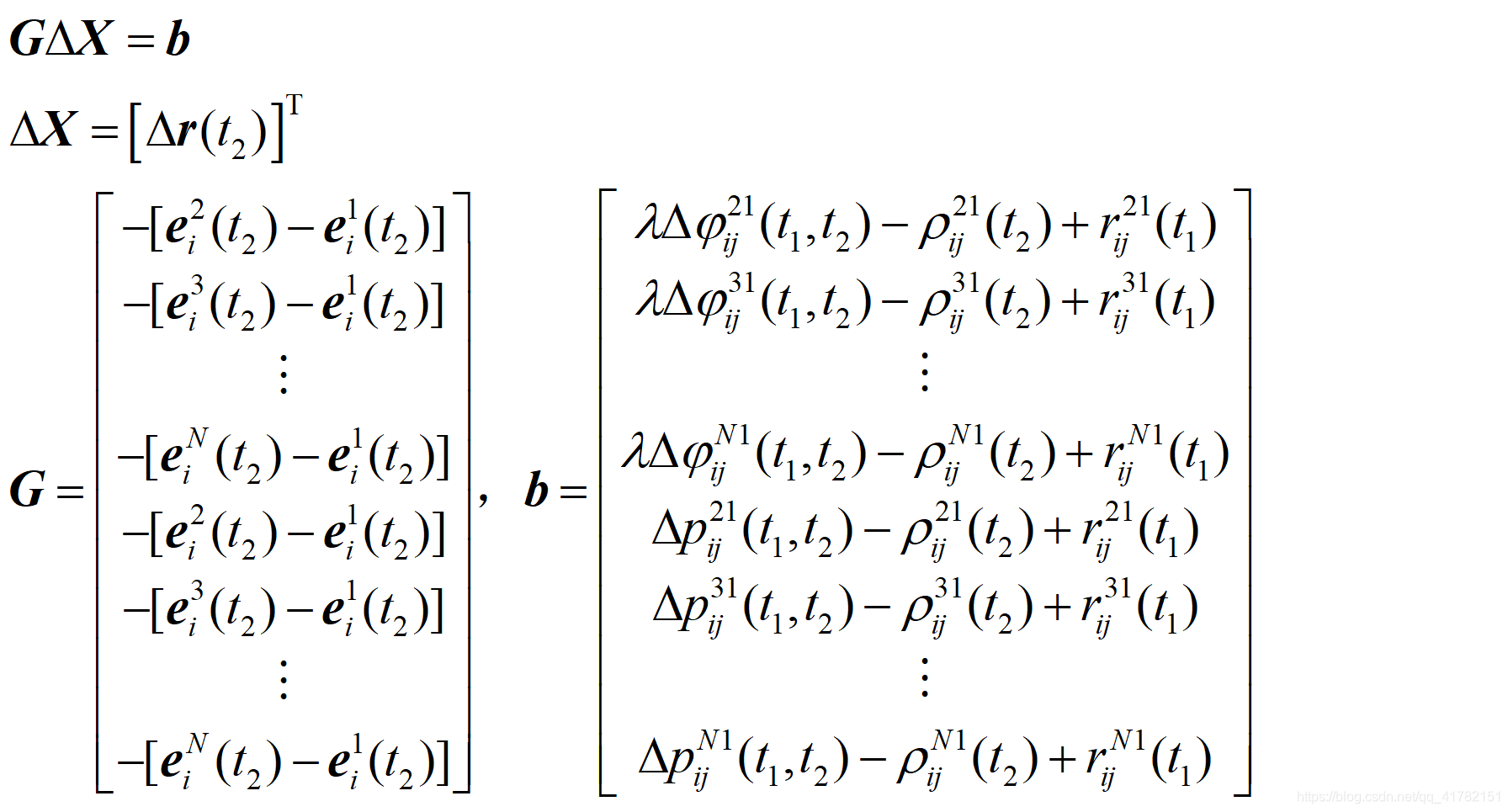
只做一次最小二乘迭代，得到此历元位置与此历元大致位置的位置误差，此位置误差再加上此历元大致位置与上一历元精确位置的误差，就得到了t1历元到t2历元的接收机位置变化量。若直接用上一历元的接收机精确位置作为此历元接收机的大致位置，那么三差求得的位置误差就是两历元间的接收机位置变化量。