边长为n的正方形最多可以放下多少个半径为r的圆？

今天看见数院群里有人在讨论一道有意思的题目，题意好像是这样的：在一个10x10的正方形里最多可以放多少个半径为1圆？在知乎里找到了10*10的正方形能放多少个直径为1的圆，那么最优的放置方法如下：

从图中可以看出，并不是每一排放10个，放10排是最优的。因为这样会造成中间的空隙很大。可以看出可能更优的放置方法是：交错着放，即（图中从下往上看）：第一排放10个，第二排放9个，第三排放10个。第二排的每一个都放在两个的中间，虽然这样第二排少放了一个，但是它给占用的高度更小了。如果一直这样放就有可能使得累计出来的高度多放一排。但是我们却不知道用减少个数来换取余留下来的高度是否是值得的。（比如下图所示：正方形边长是3，那么交错放，只能放3+2+3=8个，这样红线以下余留下来的高度不足以再放下一排）

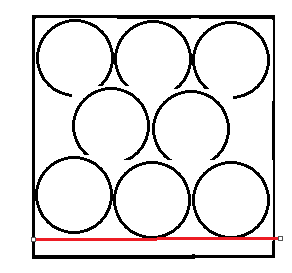
为了简化问题，只讨论正方形边长能被圆直径整除的情况。
应该怎样决策呢？现在已经确定最优的放法就是每一排要么放满n个，要么和上一排交错放，放n-1个或者n个，因为这样能最少的占用高度。
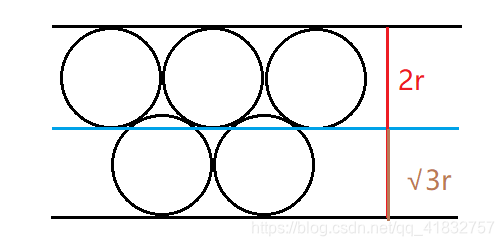
如果不交错放，那么它占用的高度就是2r。如果交错放，用勾股定理算出占用的高度是√3r。如下图所示：
这样很容易想到用动态规划来解决这个问题。因为它的决策阶段很明显被划分成了一排一排的，而每一排有2种决策方法。由于还要记录它决策过程中的高度。所以要用一维来方便计算出目前放置的高度。可以增加一个状态来表示交错放置了多少次。这样来定义状态：用f[i][j][k]来表示：前i行中，交错放置了j次，并且第i行的放置状态为k时，最多放置圆的个数。其中k只有两种取值，k=0时表示这一排放满s个，k=1时表示这一排放s-1个（其中s=n/2r）。判断是否是加错放只需要判断上一行的k和这一行的k是否不相等。同时呢，还需要计算它当前的高度，可以用g[i][j][k]来记录高度。

这样它们的这状态转移方程很容易写出来：
记每一排放满恰好能放s个。

f[i][j][0]=max(f[i-1][j-1][1]，f[i-1][j][0])+s
g[i][j][0]=g[i-1][j-1][1]+√3r ， 当f[i-1][j-1][0]<f[i-1][j][1]时
g[i][j][0]=g[i-1][j][0]+2r ， 当f[i-1][j-1][0]>f[i-1][j][1]时

解释：f[i][j][0]：前i排中交错放了j次，并且第i排放满时，最多放的个数。它可以由上一排也放满了时转移过来，因为这排和上一排都放了s个，所以加错次数不变，上一排k的状态是0，即：f[i-1][j][0]。也可以由上一行没有放满的状态，这时交错次数增加了1，上一排k的状态是1，所以由f[i-1][j-1][1]转移过来。这两者取一个最大值后加上这一排放置的个数就作为f[i][j][0]的值。高度g的计算是根据前后的k是否一样转移的（k相等，增加2r，否则增加√3r）。

同理有：
f[i][j][1]=f[i-1][j-1][0]+s-1
g[i][j][1]=g[i-1][j-1][0]+√3*r

解释：这里的转移状态只有一个，原因是当前第i排放的是s-1个，如果上一排还是放的s-1个，肯定不是最优的，因为这样不仅占用2r高，这排还少放一个，怎么也划不来。所以不用从f[i-1][j][1]转移过来。

最终答案就是所有g[i][j][k]<=n的状态中的max(f[i][j][k])

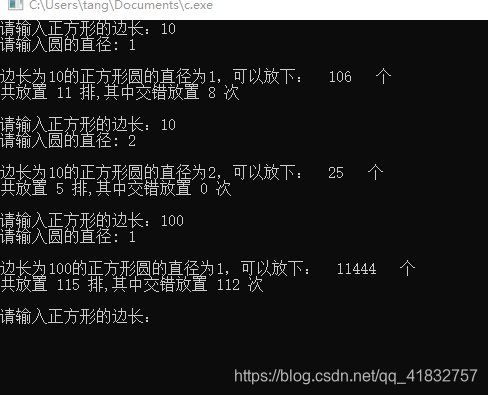
有了答案放置方法就可以倒推回去了，如10*10的正方形，直径是1的圆，最终答案是106。这个答案在f[11][8][0]里面，那么可以得出共放了11排，其中交错放置了8次。复原放法很简单，前9排交错放（共8次交错）。
即：第一排放10个，第二排放9个，第三排放10个，第四排放9个…，第九排放10个，之后的10-11排都放10个。

用c++实现如下：

#include<iostream>
#include<cstdio>
#include<math.h>
using namespace std;
const int N=500;
int f[N][N][2];
double g[N][N][2];
int main()
{
    while(true)
    {
        int n,d;
        cout<<"请输入正方形的边长：";
        cin>>n;
        cout<<"请输入圆的直径: ";
        cin>>d;
        cout<<endl;
        int nn=n;
        int D=d;
        if(d%2!=0)
            n*=2,d*=2;
        double r=d/2;
        int s=n/d;
        int ans=0;
        double sqrt3=sqrt(3);

        //cout<<n<<" "<<d<<" "<<sqrt3<<" "<<s<<endl;
        int ii,jj;
        for(int i=1; i<=n; i++)
        {
            for(int j=0; j<=i; j++)
            {

                if(j>0&&f[i-1][j-1][1]>f[i-1][j][0])
                {
                    f[i][j][0]=f[i-1][j-1][1]+s;
                    g[i][j][0]=g[i-1][j-1][1]+sqrt3*r;
                }
                else
                {
                    f[i][j][0]=f[i-1][j][0]+s;
                    g[i][j][0]=g[i-1][j][0]+2*r;
                }
                if(j>0)
                {

                    f[i][j][1]=f[i-1][j-1][0]+s-1;
                    g[i][j][1]=g[i-1][j-1][0]+sqrt3*r;
                }
                if(g[i][j][0]<=n)
                    if(ans<f[i][j][0])
                        ans=f[i][j][0],ii=i,jj=j;
                if(g[i][j][1]<=n)
                    if(ans<f[i][j][1])ans=f[i][j][1],ii=i,jj=j;
            }
        }

        printf("边长为%d的正方形圆的直径为%d，可以放下：  %d   个\n",nn,D,ans);
        printf("共放置 %d 排,其中交错放置 %d 次\n\n",ii,jj);
    }

}

经过测试，结果如下：