从正规式开始
一、先将正规式转换成NFA
通过下面的对应法则将正规式转换成NFA
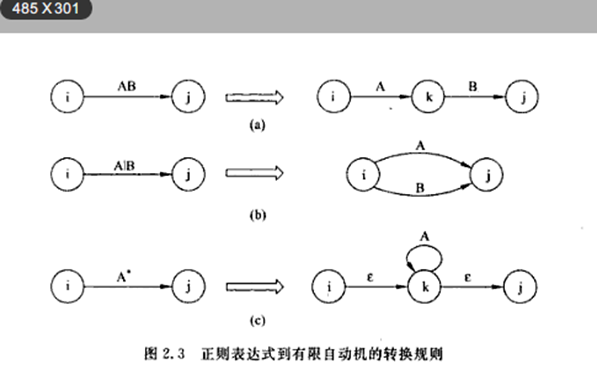
例如:
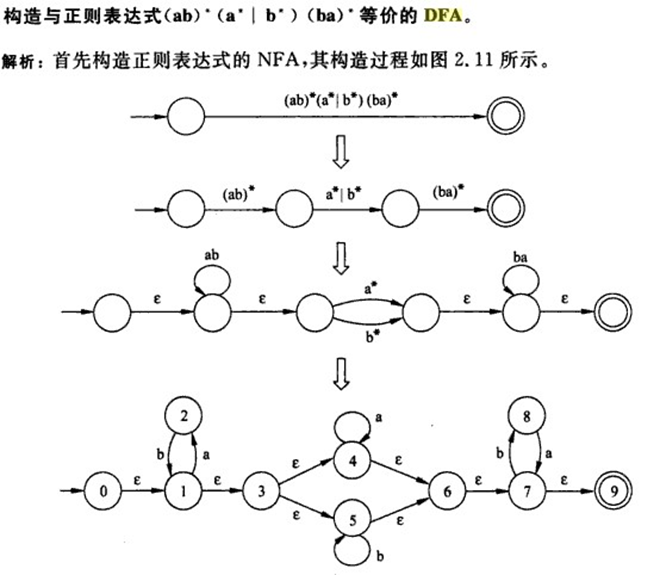
二、再将NFA转成DFA(子集法)
运用子集法的3个概念:
(1 )状态集的ε-闭包: 状态集I中的任何状态s经任意条ε弧而能到达的所有状态的集合,定义为状态集I的ε -闭包,表示为
ε
−
c
l
o
s
u
r
e
(
)
ε -closure()
ε−closure()。
(2)状态集的a弧转换: 状态集I中的任何状态s经过一条a弧而能到达的所有状态的集合,定义为状态集1的a弧转换,表示为move(l,a)。
(3)状态集的a弧转换的闭包a: l g = ε − c l o s u r e ( m o v e ( l , a ) ) lg= ε-closure(move(l,a)) lg=ε−closure(move(l,a))
上面的正规式转换成NFA:
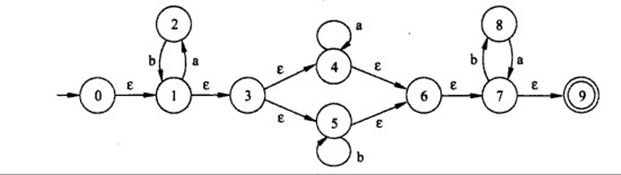
先从初态0开始求:
【因为每个状态通过一条ε弧到达自己本身,所以求得ε的闭包包含自己】
(1)求0的ε的闭包:经过任意条ε所能到达的状态,集合为{0,1,3,4,5,6,7,9}
(2)求0的a弧转换:1经过a弧到达2,4经过a弧到达4,其余没有经过一条a弧到达某个状态,所以集合为{2,4}
(3)求a弧转换的闭包:{2,4}分别经过任意条ε所能到达的状态,集合为{2,4,6,7,9}
(4)求0的b弧转换:5经过b到5,7经过b到8,,其余没有经过一条b弧到达某个状态,所以集合为{5,8}
(5)求b弧转换的闭包:{5,8}分别经过任意条ε所能到达的状态,集合为{5,6,7,8,9}
0的ε-闭包:{0,1,3,4,5,6,7,9}
0的a弧转换:{2,4}
0的a弧转换的ε-闭包:{2,4,6,7,9}
0的b弧转换:{5,8}
0的b弧转换的ε-闭包:{5,6,7,8,9}
现在列一个表格:
(1)表格的列数为输入字符的个数+1,此题为a,b两个输入字符,所以为3列。
(2)第一列第一行填写初态的ε-闭包(此题0的ε-闭包),第二列第一行填写初态的a弧转换的ε-闭包(此题0的a弧转换的ε-闭包),第三列第一行填写初态的b弧转换的ε-闭包(此题0的b弧转换的ε-闭包)…以此类推。
(3)第一列的第二行以下填入上一行第二列以后的没有出现过的状态集。(此题第一行第二列第三列都没有出现在第一列中,将他们填入第一列)
| I | I a I_a Ia | I b I_b Ib |
|---|---|---|
| {0,1,3,4,5,6,7,9} | {2,4,6,7,9} | {5,6,7,8,9} |
| {2,4,6,7,9} | ||
| {5,6,7,8,9} |
下图为填好的表:
【新的终态的判断方法就是包含原来终态的集合就为终态,例如此题原来终态为9,所以包含9的集合就为终态,[双圈代表终态];
新的初态就是包含原来初态的集合就为初态,例如此题原来初态为0,所以包含0的集合就为初态】

为表里的状态集重新标上号:

可以得到下面的图:
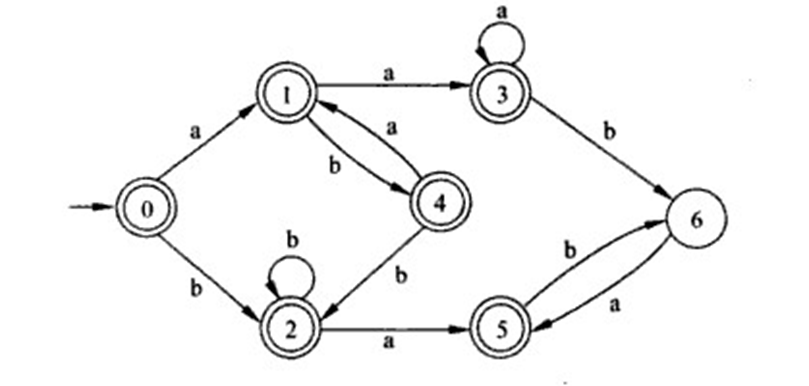
这个图是还不是最小化的DFA,还需要DFA最小化。但下面DFA最小化重新举例。
三、将DFA最小化
先了解几个概念:
1.多余状态:对于一个状态 S i S_i Si,若从开始状态出发,不可能到达改状态Si,则Si为多余(无用)状态。
2.死状态:对于一个状态Si,对于任意输入符号a,若转到它本身后,不可能从它到达终止状态,则称Si为死状态。
1,2都称为无关状态
3.等价状态:若Si为自动机的一个状态,我们把从Si出发能导出的所有符号串的集合记为L(Si)。
设有两个状态Si和Sj,若有
L
(
S
i
)
=
L
(
S
j
)
L(Si)=L(Sj)
L(Si)=L(Sj),则称Si和Sj是等价状态。
4.可区别状态:自动机中两个状态Si和Sj,如果它们不等价,则称它们可区别。
5.两个状态(Si和Sj)等价的判断条件:
(1)状态Si和Sj必须同时为终止状态或同时为非终止状态。即终止状态和非终止状态是可区别的。
(2)状态Si和Sj对于任意输入符a∈Σ,必须转到等价的状态里,否则Si和Sj是可区别的。
DFA的化简算法:对于DFA M=(S,Σ,f,S0,Z)
(1)首先将DFA的状态集进行初始化,分成Π=(Z,S-Z);
(2) 用下面的过程对Π构造新的划分Π new
for (Π中每个组G) do //每个组都是一个状态集
begin
把G划分成小组,G中的任意两个状态Si和Sj在同一组中,当且仅当对于Σ中任意输入符号a ,Si和Sj的a转换是到同一组中,move(Si,a) ∈Gi ,move(Sj,a) ∈Gi。这样,只要Si和Sj的a转换是到不同的组中,则说明Si和Sj是可区别的,可进行划分。在Π new中用刚完成的对G的划分代替原来的G。
end ; Π := Π new;
(3)重复执行(2),直到Π中每个状态集不能再划分(Π new= Π)为止;
(4)合并等价状态 ,在每个G中,取任意状态作为代表,删去其它状态;
(5)删去无关状态,从其它状态到无关状态的转换都成为无定义。
举例:
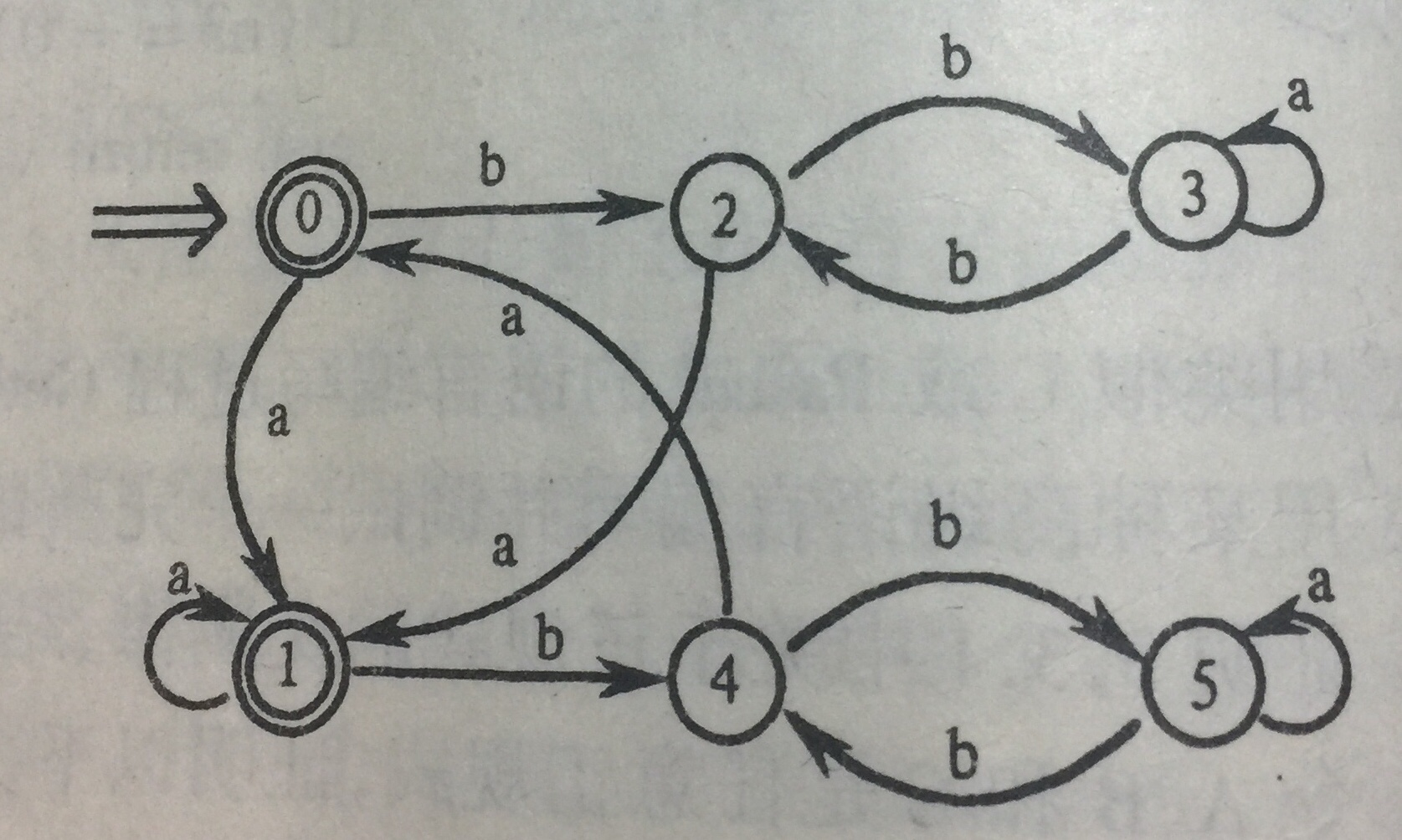
①首次划分: Π0=({2,3,4,5},{0,1})
②在G={2,3,4,5}中:f(2,a)=1,f(4,a)=0(转向终态集{0,1});f(3,a)=3,f(5,a)=5(转向非终态集{2,3,4,5}),故{2,4}和{3,5}是可区别的,得Π1=({2,4},{3,5},{0,1});
③在G={2,4}中,f(2,a)=1,f(4,a)=0(转向终态子集),而f(2,b)=3,f(4,b)=5(转向非终态子集{3,5}),所以不可区别,不再进行划分;
④考察G={3,5},f(3,a)=3,f(5,a)=5(转向非终态子集{3,5}),f(3,b)=2,f(5,b)=4(转向非终态子集{2,4}), 所以不可区别,不再进行划分;
⑤考察G={0,1},f(0,a)=f(1,a)=1(转向终态集{0,1}); f(0,b)=2,f(1,b)=4(转向非终态子集{2,4}),所以不可区别,不再进行划分;
⑦进一步进行考察,可以发现每个子集都不能再划分了;
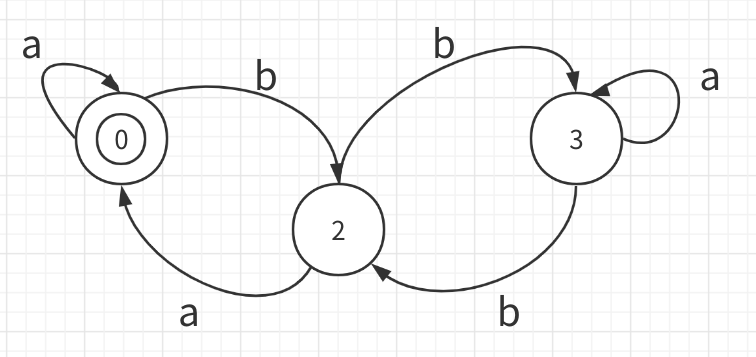
⑧消去等价状态:{0,1}用0表示,{2,4}用2表示,{3,5}用3表示,如右图所示
⑨去掉无关状态,因DFA M’中没有无关状态,所以下图即为最后结果。
























 3283
3283











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








