IoU（交并比）理解与计算

原创已于 2025-08-26 10:46:21 修改 · 399 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#python #图像处理

于 2025-07-11 14:54:31 首次发布

图像处理专栏收录该内容

5 篇文章

订阅专栏

1. 概述

IoU(Intersection over Union)被广泛应用于计算机视觉中的目标检测、图像分割等领域，用于评价预测的区域和真实标签的区域的重叠程度。简单来说，其核心思想就是两个包围框的交集和并集的比值，也就是所谓的交并比。

计算公式为：

$\text{IOU} = \frac{\text{Area of Intersection}}{\text{Area of Union}} = \frac{A \cap B}{A \cup B}$

需要稍微注意的地方在于，不同的坐标系中，获取连个包围框的交集的方法稍微有些不同，但整体上来说，

相交区域的左边界：两个矩形框左边界中的较右边
相交区域的右边界：两个矩形框右边界中的较左边
相交区域的上边界：两个矩形框上边界中的较下方
相交区域的下边界：两个矩形框下边界中的较上方

也就是说，尽量往靠近中心点附近找。

2. 在图像坐标系中

由于图像是离散的像素点组成，因此在计算面积求宽和高时，不能直接right - left和top - bottom，应该加上第一列/行。如四个像素点组成的矩形，仅用坐标相减时面积应该是1 * 1，因此，在这里，我们加上1，得到的面积为（1 + 1） * （1 + 1）。

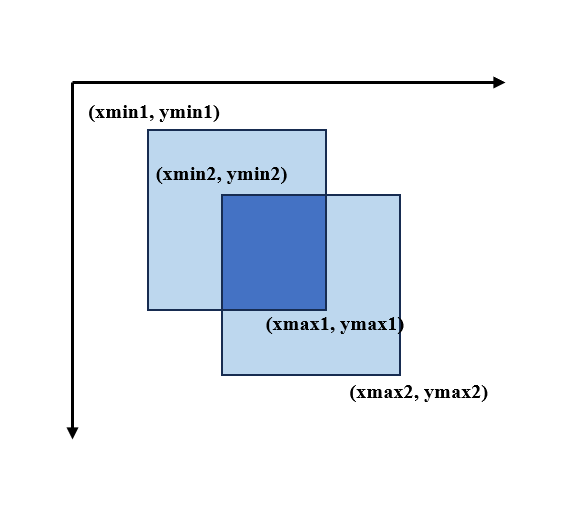
def IoU_image(box1:Union[tuple,list],box2:Union[tuple,list]) -> float:
    """
    计算图像坐标系中的IoU
    box: 左上右下， [xmin, ymin, xmax, ymax]
    """
    xmin1, ymin1, xmax1, ymax1 = box1
    xmin2, ymin2, xmax2, ymax2 = box2

    left = max(xmin1, xmin2)
    right = min(xmax1, xmax2)
    top = max(ymin1, ymin2)
    bottom = min(ymax1, ymax2)

    inter_height = max(bottom - top + 1, 0)
    inter_width = max(right - left + 1, 0)
    inter_area = inter_width * inter_height

    area1 = (xmax1 - xmin1 + 1) * (ymax1 - ymin1 + 1)
    area2 = (xmax2 - xmin2 + 1) * (ymax2 - ymin2 + 1)
    union = area1 + area2 - inter_area + 1e-5   #防止除零

    return inter_area / union

2. 在二维笛卡尔坐标系中

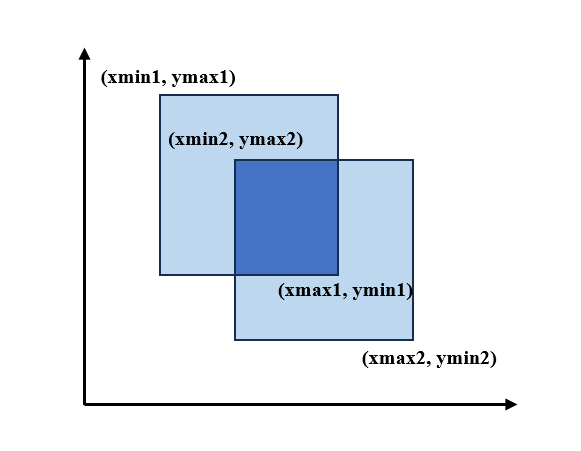
def IoU_Cartesian_Coordinates(box1:Union[tuple,list],box2:Union[tuple,list]) -> float:
    """
    笛卡尔坐标系中计算IoU
    """
    xmin1, ymax1, xmax1, ymin1 = box1
    xmin2, ymax2, xmax2, ymin2 = box2

    left = max(xmin1, xmin2)
    right = min(xmax1, xmax2)
    top = min(ymax1, ymax2)
    bottom = max(ymin1, ymin2)

    inter_height = max(top - bottom, 0)
    inter_width = max(right - left, 0)
    inter_area = inter_width * inter_height

    area1 = (xmax1 - xmin1) * (ymax1 - ymin1)
    area2 = (xmax2 - xmin2) * (ymax2 - ymin2)
    union = area1 + area2 - inter_area + 1e-5   #防止除零

    return inter_area / union

Reference：

https://zhuanlan.zhihu.com/p/473224484