matlab程序求解闭环系统谐振频率Wr、谐振峰值Mr、幅频带宽、相频带宽
本程序使用matlab脚本分析闭环系统的频率特性,画出系统的幅频特性和相频特性曲线,即闭环伯德图。并直接得出该闭环系统的频率特性指标用来分析系统的稳定性。可以得到的指标有:谐振频率Wr、谐振峰值Mr、幅频带宽、相频带宽
该闭环系统开环传递函数为
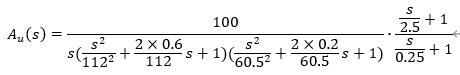
主程序脚本
num1=[1];
den1=[1/112^2 2*0.6/112 1];
G1=tf(num1,den1);
num2=[1];
den2=[1/60.5^2 2*0.2/60.5 1 0];
G2=tf(num2,den2);
num3=[1/2.5 1];
den3=[1/0.25 1];
G3=tf(num3,den3);
G_open = 100*G1*G2*G3;
G_close = feedback(G_open,1);
[Gm,Pm,Wcg,Wcp]=margin(G_open);%求解开环幅值裕度、相位裕度、穿越频率
bode(G_close);
[Mr,Wr,Wr_3db,Wr_9db] = mr(G_close);
fprintf('幅值裕度:%f\n相位裕度:%f\n穿越频率:%f\n相角交界频率:%f\n',Gm,Pm,Wcp,Wcg);
fprintf('谐振幅值:%f\n谐振频率:%f\n幅频带宽:%f\n相频带宽:%f\n',Mr,Wr,Wr_3db,Wr_9db);
grid on;
被调求解函数mr()
function [ Mr,Wr,Wr_3db,Wr_9db] = mr(G_close)
% 求解系统闭环谐振幅值Mr、谐振频率Wr
[mag,phase,w] = bode(G_close);
c = size(mag,3);
mag1 = zeros(c,1);
for i=1:c
mag1(i) = 20*log10(mag(1,1,i));%得到每个点的幅值
end
[M,i] = max(mag1);%得到最大幅值及对应频率
%显示谐振幅值和谐振频率
Mr = M;
Wr = w(i);
%显示-3dB截止频率
Wr_3db = interp1(mag1,w,-3,'Newton');%插值法求解
c = size(phase,3);
pha1 = zeros(c,1);
for i=1:c
pha1(i) = phase(1,1,i);%得到每一个点的频率
end
Wr_9db = interp1(pha1,w,-90,'Newton');%插值法求解
end
-------------------------------------------------欢迎使用并优化-----------------------------------------------------------------------
程序运行结果如下所示:
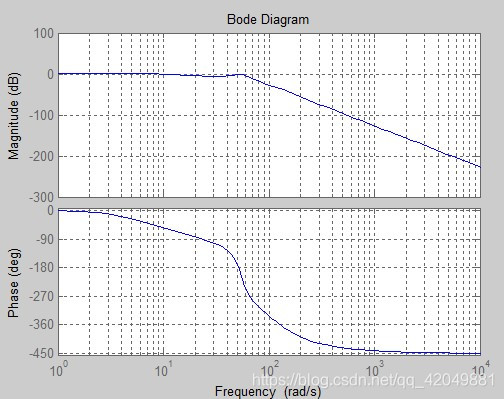
幅值裕度:2.160824
相位裕度:67.407345
穿越频率:10.595368
相角交界频率:51.852456
谐振幅值:1.239164
谐振频率:3.850372
幅频带宽:15.555650
相频带宽:24.775171
























 1883
1883

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








