风速Weibull分布和光伏Beta分布之运用场景法描述分布式电源的出力的不确定性

概述

运用场景法来描述分布式电源出力的不确定性，采用Weibull分布和Beta分布分别构建风速和光照强度模型，通过分布式电源出力公式，将随机问题转换为确定性问题；然后采用蒙特卡洛模拟法抽样和Kmeans聚类算法将样本聚类成3个典型场景。

1  分布式电源出力模型

1.1  风电机组出力模型

针对风速建模主要有Weibul分布、Rayleigh分布、Gamma分布[1]等。

选择某地风电站全年风速数据样本，分别采用上述三种分布对风速数据采用线性回归进行拟合，拟合结果如图1（1）所示，在图中尾部可以清晰反映出Weibull分布拟合的效果良好。

采用风速近似服从Weibull分布，即

                      

                      

式中：v为风速(m/s)；λ、ρ为Weibull分布的两个参数。参数的确定由实际数据进行拟合得到。

在建立了合适的风速模型后，根据风速数据换算出风电机组有功出力

            

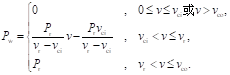
式中：vci为切入风速；vco为切出风速；vr为风电机组额定风速；Pr为风电机组的额定输出功率。

1.2  太阳能光伏电站出力模型

针对太阳光照强度进行建模，应用最为广泛的有Beta分布和正态分布。

选择某地光伏电站全年6:00-17:00太阳光照强度数据样本，用上述两种分布采用线性方法进行拟合，结果如图1（2）所示，可以清晰的反映出Beta分布拟合太阳光照强度要优于正态分布。

本文采用太阳光照强度近似服从Beta分布，即

          

          

式中：r为光照强度(W/m2)；Γ()为Gamma函数；rmax为最大光照强度；α、β为Beta分布的两个参数。参数的确定由实际数据进行拟合得到。

在确定太阳光照强度之后，可得太阳能光伏机组的输出功率

                              

                      

式中：A为每块太阳能电池板的面积；η为太阳能转换为电能的效率。

（1）风速

（2）光照强度

图1  风速与光照强度拟合图

2  基于场景法的随机潮流计算

2.1  场景生成

首先利用蒙特卡洛模拟法对上文立的模型进行1 000次抽样，得到a×b矩阵N，其中a为抽样次数（1 000），b为24（一天等分24个时间段），并将每次抽样的结果定义为场景，即生成了1 000个分布式电源的出力场景。分布式接入配电网的数量很少，且DG的额定功率较小，不参与电压的调节，同时DG出力维持在额定功率以下；故DG以PQ节点（功率因数为0.9）的形式接入配电网。

2.2  基于手肘法与K均值聚类算法场景缩减

由于抽样数目过多，为更好解决精度和速度带来问题，对所生成的样本采用K均值聚类算法处理得到典型的k个场景。步骤如下：

a) 在矩阵N中随机选取k行作为初始聚类中心得到k×b矩阵Ml，其中k=3，初始迭代次数l=1；光样本数据类比于此。

b) 计算每组样本数据与每组聚类中心的距离

   式中Dij为聚类中心矩阵Ml第j组Ml(j)中心 与样本矩阵N第i组数据N(i)之间的距离。并将每组样本数据归入与之距离最近的簇W(j)中，每个簇W(j)所含样本数为c(j)。

c) 按照下式计算每组所有样本均值向量来更新原来每组的聚类中心：

                         

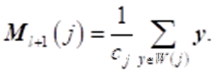
d) 如不满足下式重复上述步骤，直至满足。

               

            

e) 则聚类后风场景概率为

                     

采用同样方法得到光场景概率Isolar,j(j=1,2,3)。

f) 综合场景概率

 然而K均值聚类算法有一个主要缺陷：需要确定k值，本文先采用手肘法则将值确定，再使用上述流程进行场景聚类。手肘法则的核心指标是误差平方和（sum of squares due to error，SSE），定义为：

             

在此基础上，还有轮廓系数（Silhouette）[17]和Calinski-Harabasz（CH）指标[18]。轮廓系数和CH指标则是考虑簇内样本的紧密性和不同簇之间的可分性。轮廓系数

                               

式中：A为一个样本点到所属簇中其他样本点的平均距离；B为一个样本点到其他簇中所有样本点平均距离的最小值。

CH指标：

式中z为整个数据集的中心。

1 000个时间序列场景聚类为5个场景对应概率见表2。

表2  5个场景下对应的概率

场景	风场景 概率	光场景 概率	概率
1	0.310	0.425	0.311
2	0.411	0.251	0.328
3	0.262	0.309	0.285
4	0.221	0.201	0.317
5	0.251	0.319	0.242

 3  运行结果

参考文献

[1]李慧,孙宏斌,张芳.风电场风速分布模型研究综述[J].电工电能新技术,2014,33(8):62-66.
[2]管霖,陈旭,吕耀棠, 等.适用于电网规划的光伏发电概率模型及其应用[J].电力自动化设备,2017,37(11):1-7.
[3]方斯顿,程浩忠,宋越, 等.基于样条重构和准蒙特卡洛的随机潮流方法[J].高电压技术,2015,41(10):3447-3453.
[4]齐晖,程韧俐,史军,等. 采用最优场景法求解含风电的无功优化模型[J]. 广东电力，2019，32(6）：18-28.