谱图理论（Spectral and Algebraic Graph Theory）| Chapter2: Eigenvalues and Optimization

上期介绍了谱图中的矩阵表示，其中矩阵M具有spreadsheet和operator的作用。当矩阵M作为做操作算子时，可以实现：（1）概率转移，；（2）将向量x转化为一个数(矩阵的二次型），。

接下来，我们首先围绕矩阵的二次型给出了瑞丽熵的定义，并谱定理来证明Courant Fischer定理。然后，我们以与Courant Fischer几乎相同的形式证明了谱定理。

一、瑞丽熵

向量x相对于矩阵M的瑞丽熵定义为： 特征向量的瑞丽熵是其特征值：如果，则

瑞丽熵的定义为矩阵M关于向量ψ的二次型，并且对其做了归一化，以去除向量ψ模长对瑞丽熵的影响。

二、Courant-Fischer Theorem

Courant-Fischer定理告诉我们，使瑞丽熵最大化的向量x正是M的最大特征值的特征向量。事实上，它提供了对称矩阵所有特征值的类似特征。

2.1 Courant Fischer定理

定理2.1（Courant Fischer定理）设M是特征值为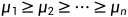的对称矩阵。然后，

其中最大化和最小化在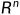的子空间S和T上。

假设k=1，则 上式可写为

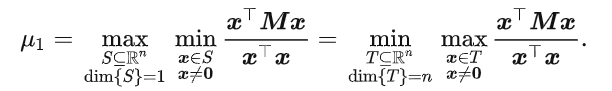
此时，左半边S是一维空间，所以空间里任意向量方向相同或者相反，所以矩阵M关于该空间内任意向量的瑞丽熵都相同（S空间中任意向量对矩阵M对的转化方向均相同，且瑞丽熵的分母去除了向量x长度对与瑞丽熵数值的影响）。所以，对于n维空间的各向量，矩阵M最大特征值对应的特征向量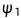，能使矩阵M的瑞丽熵取到最大值，即为。

右半边T是n维空间，对于中的任意向量，空间T存在与之方向相同的向量。右半边min符号并未起到实际作用。即在n维空间中，使瑞丽熵取到最大值的向量，为与特征向量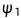平行的向量。

2.2 证明一

2.2 证明2（谱定理的证明）

定理2.2 设M是对称矩阵，设x是M的瑞丽熵取最大值时的非零向量，则，其中是M的最大特征值。相反，最小值由M的最小特征值的特征向量实现。

证明：由于瑞丽熵是齐次的，所以考虑单位向量x就足够了。由于单位向量的集合是一个封闭且紧凑的集合，因此在这个集合上达到了最大值。设x是最大化瑞利商的非零向量，则有：

所以：

.

若使梯度为0，则

.

即，所以对应矩阵M的一个特征值。所以，取最大值时应对应M的最大特征值，即。

接下来，通过将这个特征推广到M的所有特征值来证明谱定理。

定理2.3 设M是n维实对称矩阵。和正交单位向量，使得。此外，

并且，对于任意 ，有

类似地，

证明：

三、注意

通过最大化或最小化瑞利商来表征特征值仅适用于对称矩阵。非对称矩阵A的近似量是A的奇异向量和奇异值，即和的特征向量，以及这些矩阵的特征值的平方根。

四、总结

本节介绍了瑞丽熵的定义，以及瑞丽熵的极值与矩阵特征向量和特征值的关系。