上一期,我们介绍一下拉普拉斯矩阵L的物理意义,以及如何用拉普拉斯矩阵的特征值进行绘图。在本期中,我们研究了图的邻接矩阵的最小和最大特征值的含义。注意,邻接矩阵的最大特征值对应于拉普拉斯算子的最小特征值。Perron-Frobenius理论告诉我们,邻接矩阵的最高特征向量是非负的,其值是最小特征值绝对值的上界。当图是二分图时,它们正好相等。此外,我们还将解释最大邻接特征值与图中顶点度数之间的关系。
一、邻接矩阵
设M是图G的邻接矩阵,作为算子,M作用于向量x:

设邻接矩阵M的特征值为 ,但是,我们按照与拉普拉斯算子相反的方向排列它们,
,但是,我们按照与拉普拉斯算子相反的方向排列它们,

这样做的原因是 对应于第i个拉普拉斯特征值
对应于第i个拉普拉斯特征值 。如果G是一个d正则图,则D=Id,L=Id-M,
。如果G是一个d正则图,则D=Id,L=Id-M,
所以: .
.
因此,d正则图的最大邻接特征值是d,其对应的特征向量是常数向量。
二、最大特征值
现在,我们来看一些那些不一定是正则图中的 。设G是一个图,设
。设G是一个图,设 是G中一个顶点的最大度,设
是G中一个顶点的最大度,设 是G中顶点的平均度。
是G中顶点的平均度。
定理2.1  .
.
证明:通过考虑全1向量的瑞丽熵,下界如下:
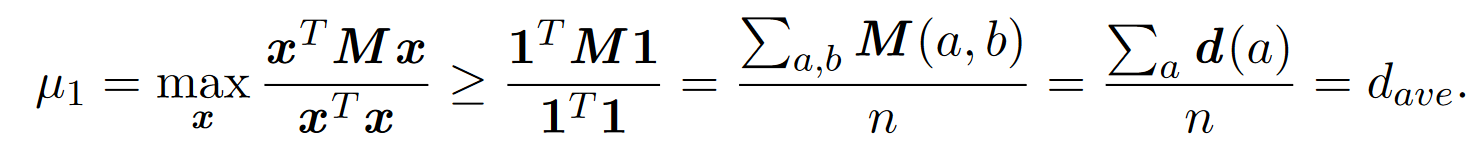
为了证明上界,设 是特征值
是特征值 的特征向量,设a为
的特征向量,设a为 取其最大值的顶点,所以
取其最大值的顶点,所以 ,并且我们可以假设
,并且我们可以假设 (如果
(如果 严格为负,则使用
严格为负,则使用 )。我们有:
)。我们有:

引理2.2 如果G是连通的并且 ,则G是
,则G是 正则的.
正则的.
证明:如果我们有上式中等式的,那么对于所有 ,
, 和
和 。因此,我们可以对a的每个邻居应用相同的理论。 当图被连接时,我们可以继续将这个参数应用于顶点的邻居。
。因此,我们可以对a的每个邻居应用相同的理论。 当图被连接时,我们可以继续将这个参数应用于顶点的邻居。
三、特征值交错
对于图 和
和 ,我们定义由S构成的子图,写为G(S),是具有顶点集S和E中连接S中顶点的所有边的图:
,我们定义由S构成的子图,写为G(S),是具有顶点集S和E中连接S中顶点的所有边的图:
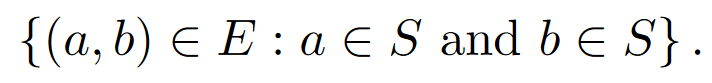
对于行和列由集合V和 索引的对称矩阵M,我们为行和列在S中的对称子矩阵写M(S).
索引的对称矩阵M,我们为行和列在S中的对称子矩阵写M(S).
定理3.1(Cauchy's Interlacing定理)设A是n乘n对称矩阵,设B是维数为n−1的A的主子矩阵(即,B是通过从A中删除相同的行和列而获得的),则

其中 和
和 分别是A和B的特征值.
分别是A和B的特征值.
证明:在不失一般性的情况下,我们将假设B是通过移除其第一行和第一列而从A获得的。所以,通过Courant-Fischer定理可知:
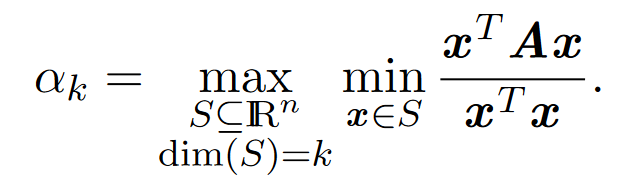

可以看到右边的表达式在一个维度为k的子空间上取最大值。由于维度k的所有子空间上的最大值只能更大,所以有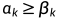 .
.
四、Wilf定理
图的着色是将颜色分配给相邻顶点具有不同颜色的顶点。如果一个图只能用k种颜色着色,那么它就被称为k可着色,图的色数,写为 。
。
定理4.1  .
.
证明:我们通过对图中顶点数的归纳来证明这一点。首先考虑具有一个顶点而没有边的图。它具有色数1和最大特征值零2。现在,假设该定理对n−1个顶点上的所有图都成立,并且设G是n个顶点上一个图。根据定理2.1,G有一个至多 的度顶点。设a是这样的顶点,并设S=V\{a}。根据定理3.1,G(S)的最大特征值最多为
的度顶点。设a是这样的顶点,并设S=V\{a}。根据定理3.1,G(S)的最大特征值最多为 ,因此我们的归纳假设G(S)的着色最多为
,因此我们的归纳假设G(S)的着色最多为 色。设c是任何这样的着色。我们只需要证明我们可以将c扩展到a。由于a最多有
色。设c是任何这样的着色。我们只需要证明我们可以将c扩展到a。由于a最多有 个邻居,因此在{1,…,
个邻居,因此在{1,…, }中有一些颜色不会在其邻居中出现,并且可以分配给它。因此,G具有
}中有一些颜色不会在其邻居中出现,并且可以分配给它。因此,G具有 的着色。
的着色。
五、对称矩阵的Perron-Frobenius定理
图的邻接矩阵的最大特征值相对应的特征向量通常不是常数向量。然而,如果图是连通的,则它总是一个正向量。
定理5.1(Perron-Frobenius, Symmetric Case)设G为连通加权图,设M为其邻接矩阵,μ1≥μ2≥···≥μn为其特征值。然后,

在证明定理5.1之前,我们将证明将用于证明的引理。它表示连通图的非负邻接矩阵的非负特征向量必须是严格正的。
引理5.2 设G是连通加权图(具有非负边权重),设M为其邻接矩阵,并假设某个非负向量 是M的特征向量。那么,
是M的特征向量。那么, 是严格正的。
是严格正的。
证明:如果 不是严格正的,则存在
不是严格正的,则存在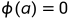 的顶点a。当G是连通的时,必须有
的顶点a。当G是连通的时,必须有 但
但 的边(b,c)。设μ为
的边(b,c)。设μ为 的特征值。当
的特征值。当 时,存在以下矛盾:
时,存在以下矛盾:

因此,我们得出结论, 必须是严格正的。
必须是严格正的。
设 是范数1的μ1的特征向量,并构造向量x,使得对所有u,
是范数1的μ1的特征向量,并构造向量x,使得对所有u, 。接下来,我们将证明x是特征值μ1的特征向量。我们有
。接下来,我们将证明x是特征值μ1的特征向量。我们有 ,此外,
,此外,

所以,x的瑞丽熵至少为 。
。
设 为
为 的特征向量,设y为
的特征向量,设y为 的向量。可以证明:
的向量。可以证明:

为了证明μ1的多重性为1(即μ2<μ1),考虑特征向量 。由于
。由于 与
与 正交,因此它必须同时包含正值和负值。我们现在构造向量y,使得
正交,因此它必须同时包含正值和负值。我们现在构造向量y,使得 ,并重复我们对x使用的论证。我们发现
,并重复我们对x使用的论证。我们发现

如果μ2=μ1,则y是特征值μ1的非负特征向量,因此引理5.2表示它是严格正的。因此, 没有任何零条目。由于它既有正条目,也有负条目,并且图是连通的,因此必须存在
没有任何零条目。由于它既有正条目,也有负条目,并且图是连通的,因此必须存在 的某条边(a,b)。那么上述不等式必须严格,因为边(a,b)将对
的某条边(a,b)。那么上述不等式必须严格,因为边(a,b)将对 作出负贡献,对
作出负贡献,对 作出正贡献。这与我们的假设μ2=μ1相矛盾。
作出正贡献。这与我们的假设μ2=μ1相矛盾。
最后,我们证明对于连通图G, 当且仅当G是二分图 .
当且仅当G是二分图 .
定理5.3 如果G是连通图且 ,则G是二分图。
,则G是二分图。
考虑实现等式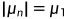 所需的条件。首先,y必须是特征值μ1的特征向量。因此,y必须是严格正的,
所需的条件。首先,y必须是特征值μ1的特征向量。因此,y必须是严格正的, 不能有任何零值,并且必须有
不能有任何零值,并且必须有 的边(a,b)。此外,
的边(a,b)。此外,

具有相同的符号,这个符号必须是负的。因此,对于每条边(a,b), 和
和 必须具有不同的符号。
必须具有不同的符号。
定理5.4如果G是二分的,则其邻接矩阵的特征值关于零是对称的。
证明:由于G是二分的,我们可以将其顶点划分为集合S和T,使得所有边都位于S和T之间。设 是具有特征值μ的M的特征向量。定义向量x :
是具有特征值μ的M的特征向量。定义向量x :

因为x是特征值为μ的特征向量,对于a∈S,

我们可以类似地证明,对于a∈T,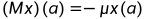 。
。
























 119
119

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








