上期介绍了矩阵的瑞丽熵的定义,以及瑞丽熵的极值与矩阵特征向量/特征值的关系。接下来,我们介绍一下拉普拉斯矩阵L的物理意义,以及如何用拉普拉斯矩阵的特征值进行绘图。
一、拉普拉斯矩阵
1.1拉普拉斯矩阵计算
带权图G的拉普拉斯矩阵二次型为:
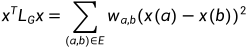 .
.
接下来,我们使用这个二次型来推导矩阵结构。假设图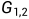 表示有两个顶点和一条边的图,我们有:
表示有两个顶点和一条边的图,我们有:
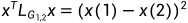 .
.
假设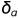 表示在坐标a处为1的基本单位向量,则:
表示在坐标a处为1的基本单位向量,则:
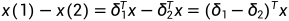 .
.
所以:
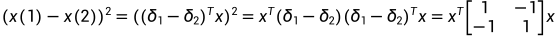 .
.
因此,
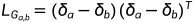 .
.
对所有边求和:
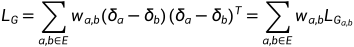
1.2 连通性
引理1 设G=(V,E)是一个图,设0=λ1≤λ2≤··≤λn为拉普拉斯矩阵L的特征值,那么,λ2>0当且仅当G是连通的。
证明:我们首先证明如果G是不连通的,λ2=0。如果G是不连通的,那么它可以被描述为两个图G1和G2的并集。在适当地重新排序顶点之后,我们可以写为:
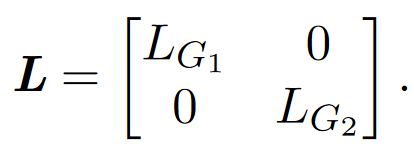
因此,L具有至少两个特征值为零的正交特征向量: 和
和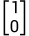 。
。
另一方面,假设G是连通的,并且ψ是特征值0的L的特征向量,即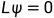 .
.
所以:
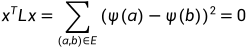 .
.
因此,对于由边连接的每对顶点(a,b),我们有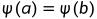 。由于每对顶点a和b都由一条路径连接,我们可以使用归纳方法来证明所有顶点a和b的
。由于每对顶点a和b都由一条路径连接,我们可以使用归纳方法来证明所有顶点a和b的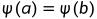 。因此,ψ必须是一个常数向量。
。因此,ψ必须是一个常数向量。
二、利用拉普拉斯特征值绘图
我们首先考虑在直线上绘制图形的问题。也就是说,将每个顶点映射到一个实数。设x是描述给每个顶点映射到实数的向量。我们希望相邻的顶点彼此靠近。
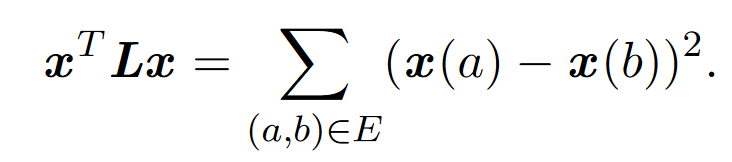
除非我们对x设置限制,否则解将退化。例如,所有顶点都可以映射到0。为了避免这种情况,我们有
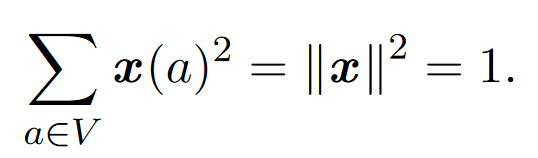
即使有这种限制,另一个退化的也是可能的:可能每个顶点都映射到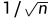 。为了防止这种情况发生,我们施加了额外的限制:
。为了防止这种情况发生,我们施加了额外的限制:
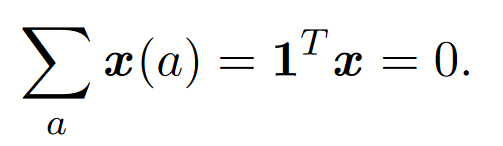
如果我们想画一个二维图,需要给出每个顶点指定两个坐标,即x和y。我们将最小化embedding中边缘长度的平方和:
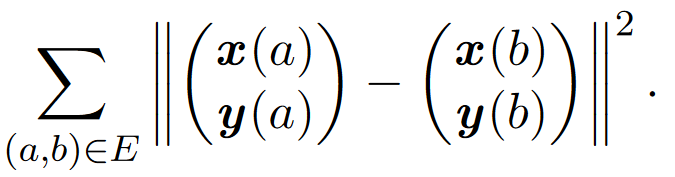
上式等于:
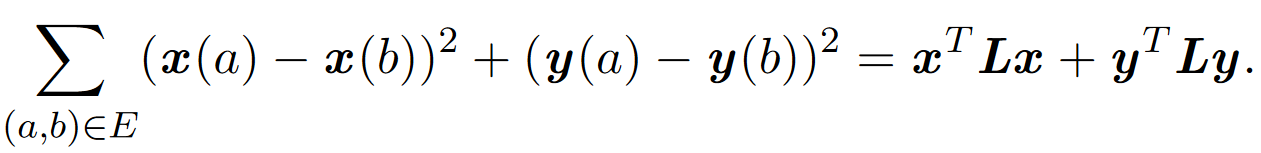
接下来,我们为x、y进添加约束条件,
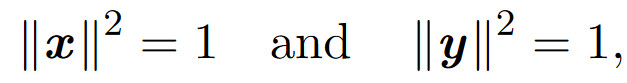
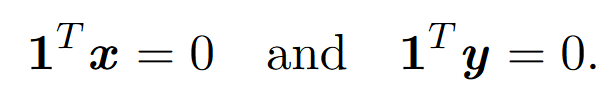
然而,这仍然可能出现退化解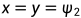 。为了确保两个坐标不同,引入了x与y正交的限制。为了在k维中嵌入图,我们找到k个正交向量
。为了确保两个坐标不同,引入了x与y正交的限制。为了在k维中嵌入图,我们找到k个正交向量 正交于1并最小化
正交于1并最小化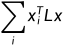 。我们自然而然得想到了
。我们自然而然得想到了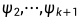 ,这种选择可以实现目标函数值
,这种选择可以实现目标函数值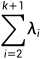 。
。
接下来的定理说明了这种选择可以实现最优解。
定理2 设L是拉普拉斯矩阵, 是所有正交于1的正交向量,然后
是所有正交于1的正交向量,然后
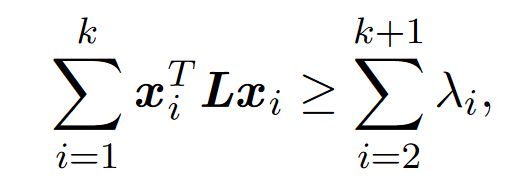
只有当所有j的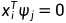 ,
,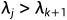 时成立。
时成立。
证明:为了不失一般性,设ψ1为常数向量。设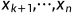 是正交基。对于所有1≤i≤n,
是正交基。对于所有1≤i≤n,
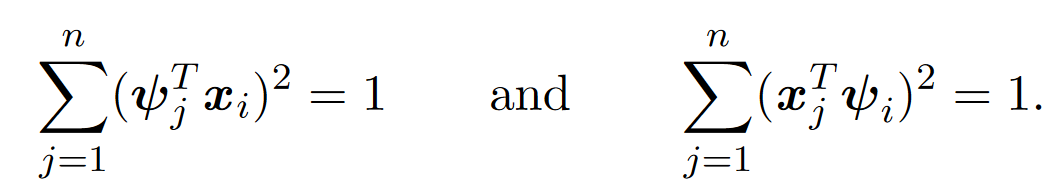
因为 ,所以
,所以
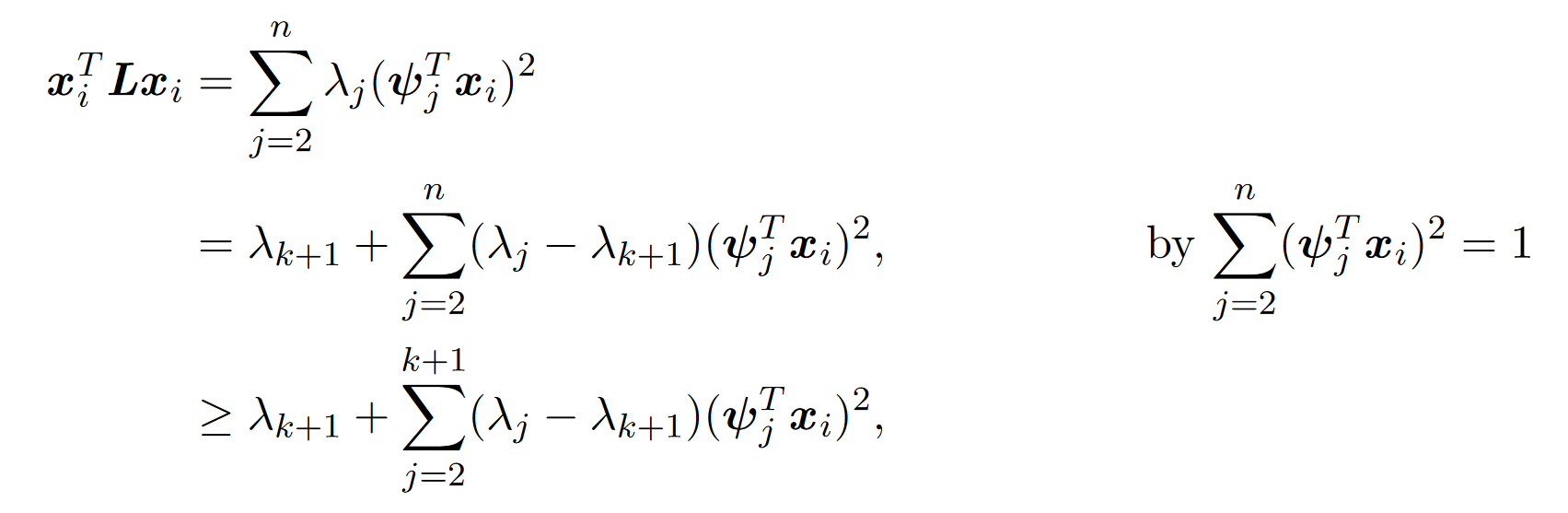
当j>k+1时,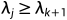 。只有当
。只有当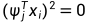 ,
,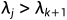 时,这个不等式才是紧的。
时,这个不等式才是紧的。
对每个i求和,得到
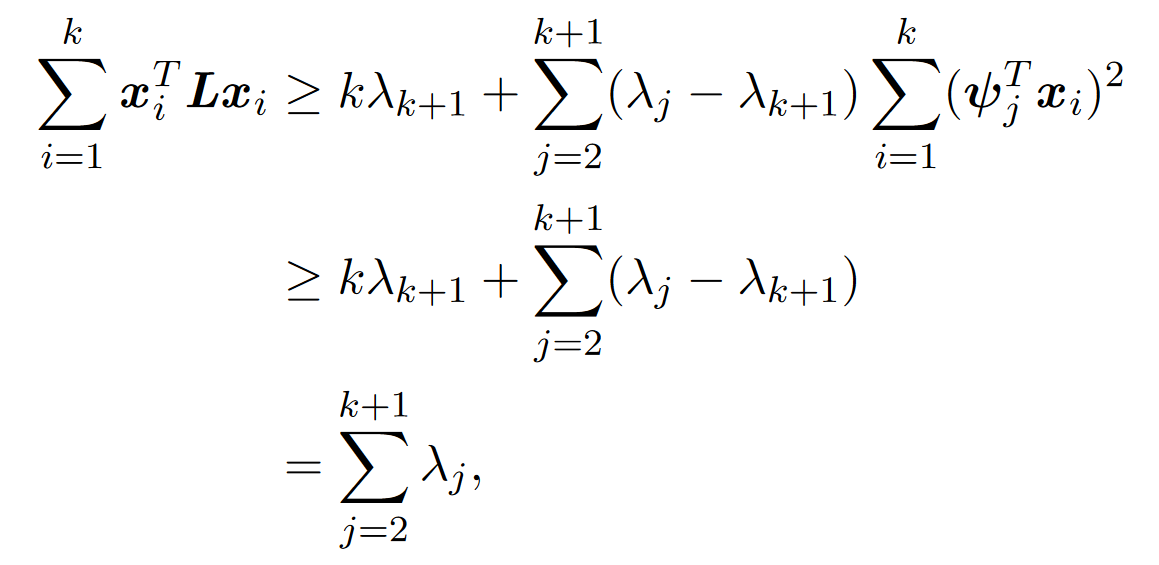
其中不等式满足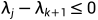 和
和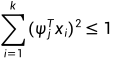 。
。






















 3208
3208











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








