针对连续变量长尾严重的解决办法

这里所说的长尾就是指某个或某几个连续变量的数值分布差别很大，呈现长尾图的样式。

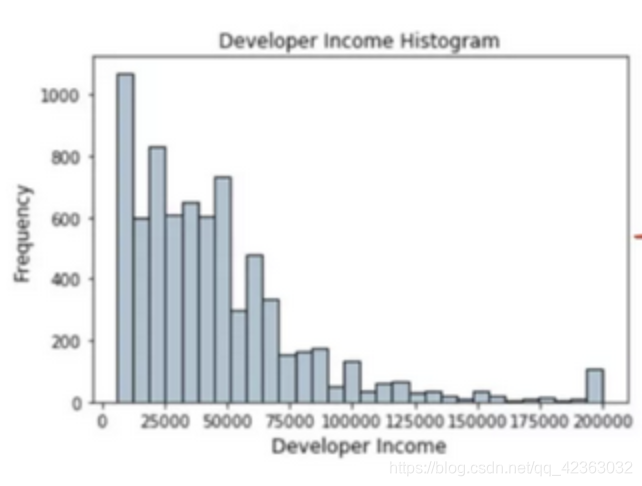
类似这种。

两种办法可以考虑，一个是对数变换，另一个就是Box-Cox变换。

或许很多人会问，分箱或者归一化不行吗，针对这种问题，分箱是不恰当的，归一化也还是原来的分布。

log变换

Log变换通常用来创建单调的数据变换。它的主要作用在于帮助稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。

当应用于倾斜分布时 Log 变换是很有用的，因为Log变换倾向于拉伸那些落在较低的幅度范围内自变量值的范围，倾向于压缩或减少更高幅度范围内的自变量值的范围。从而使得倾斜分布尽可能的接近正态分布。

针对一些数值连续特征的方差不稳定，特征值重尾分布我们需要采用Log化来调整整个数据分布的方差，属于方差稳定型数据转换。比如在词频统计中，有些介词的出现数量远远高于其他词，这种词频分布的特征就会现有些词频特征值极不协调的状况，拉大了整个数据分布的方差。这个时候，可以考虑Log化。尤其在分本分析领域，时间序列分析领域，Log化非常常见, 其目标是让方差稳定，把目标关注在其波动之上。

fcc_survey_df['Income_log'] = np.log((1+fcc_survey_df['Income']))

# or

X['impressions_log'] = X['impressions'].apply(lambda x: np.around(np.log(x), decimals=4)).replace(-np.inf, 0)

Box-Cox变换

Box-Cox 变换是另一个流行的幂变换函数簇中的一个函数。该函数有一个前提条件，即数值型值必须先变换为正数（与 log 变换所要求的一样）。万一出现数值是负的，使用一个常数对数值进行偏移是有帮助的。

生成的变换后的输出y是输入 x 和变换参数的函数；当 λ=0 时，该变换就是自然对数 log 变换，前面我们已经提到过了。λ 的最佳取值通常由最大似然或最大对数似然确定。

Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法，是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的。

import scipy.stats as spstats
# 从数据分布中移除非零值
income = np.array(fcc_survey_df['Income'])
income_clean = income[~np.isnan(income)]
# 计算最佳λ值
l, opt_lambda = spstats.boxcox(income_clean)
print('Optimal lambda value:', opt_lambda)
 
# 进行Box-Cox变换
fcc_survey_df['Income_boxcox_lambda_opt'] = spstats.boxcox(fcc_survey_df['Income'],lmbda=opt_lambda)

http://snap.stanford.edu/class/cs224w-readings/goel10longtail.pdf

https://blog.csdn.net/ningyanggege/article/details/105811065?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242