1. 梯度下降
1.1 等高线的概念
首先看下图,很多学生可能对于等高线的定义都不是太清楚,首先我们先搞清楚等高线是个什么东西。
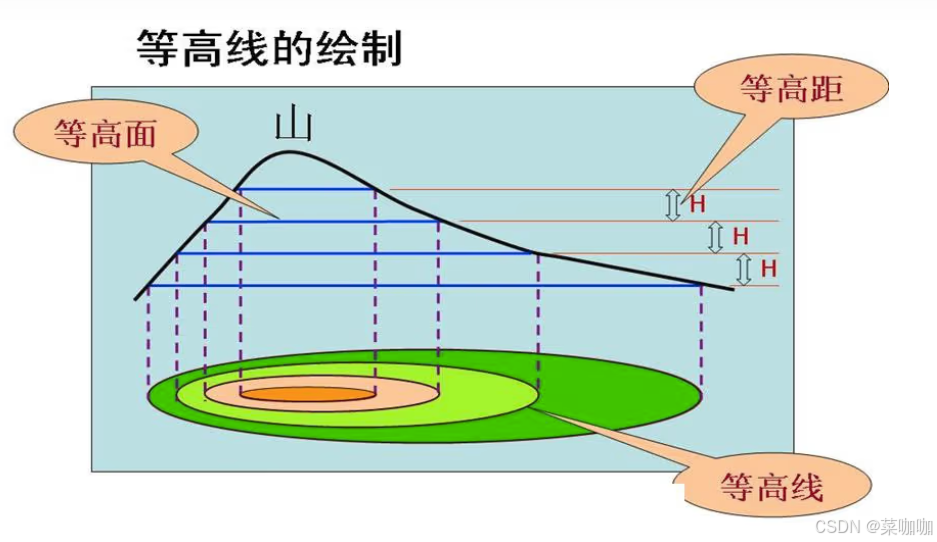
图1 等高线示意图
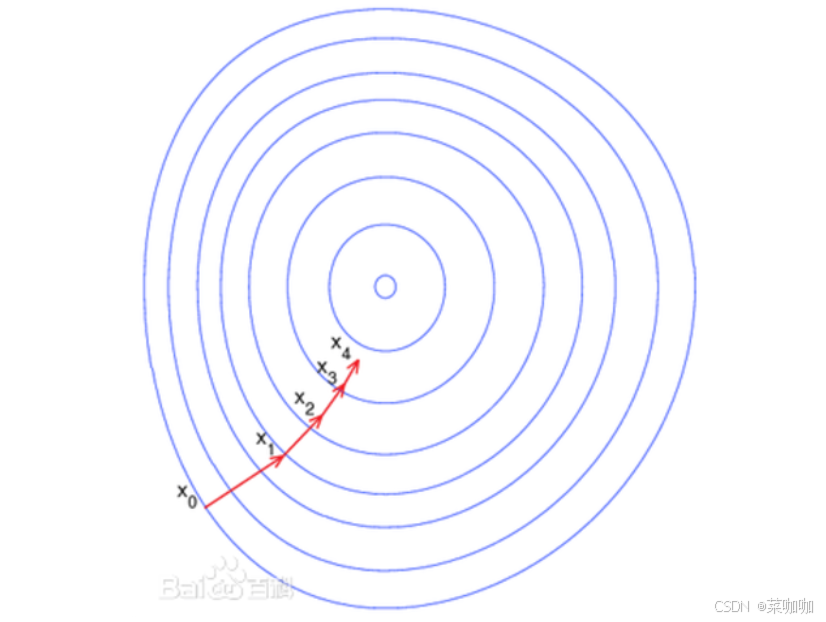
图2 等高线中的梯度走向
1.2 梯度方向为什么与等高线切线方向垂直?
有很多人可能有一个疑问,那就是梯度方向为什么是与等高线方向垂直的呢?
关于这部分的数学证明,网上有很多可以参考的资料,这里就不多做赘述,这里只谈论我本人的个人理解,以下图黄色圆圈为例:

1. 黄色圆圈上所有的点数值(函数结果)都一样
2. 既然数值一样那在整个黄色圆圈上数值都不会变化
3. 那对应于梯度来讲的话,黄色圆圈上任意一点的斜率为0
4. 那么梯度是什么?梯度是函数值增加最快的方向
5. 那梯度怎么才能变化最快呢?垂直于黄色圆圈上切线的方向变化最快
6. 所以梯度方向垂直于等高线
2. 拉格朗日函数
拉格朗日乘子法在众多领域都有广泛应用。最初它是为解决力学中的约束问题而提出的。在经典力学中,许多物体的运动受到各种约束条件的限制。例如,一个质点被限制在一个曲面上运动,或者多个质点之间存在着某种连接关系,使得它们的运动相互制约。拉格朗日乘子法能够将这些约束条件纳入到力学系统的分析中,通过引入拉格朗日乘子,将有约束的力学问题转化为无约束的变分问题,从而方便地求解物体的运动方程。
随着科学技术的发展,其应用范围不断扩大。在数学领域,常常需要在满足一定约束条件下求函数的极值。例如,求一个多元函数在某些等式约束下的最大值或最小值。拉格朗日乘子法为解决这类问题提供了一种通用的方法,它将约束条件与目标函数相结合,构造出拉格朗日函数,通过求解拉格朗日函数的驻点来找到原问题的可能极值点。
此外,在经济学中,可用于求解消费者在预算约束下的效用最大化问题,或者生产者在成本约束下的利润最大化问题;在工程学中,可用于结构优化设计、资源分配等问题;在计算机科学的机器学习领域,拉格朗日乘子法也被用于支持向量机等算法中的优化问题。
拉格朗日函数的本质:去约束
2.1 拉格朗日乘子法的基本概念

ps:对于约束函数 的理解不要单纯局限于变量,可以通过一下这个数学应用实例来进行更深一步的理解。
2.2 拉格朗日乘子法的数学应用实例
2.2.1 问题描述
假设我们要设计一个矩形,已知其周长 P 固定,需要找到长 x 和宽 y 的值,使得矩形的面积 A 最大。
2.2.2 数学建模
目标函数:矩形的面积 ,我们希望最大化这个函数。
约束条件:矩形的周长 是固定值,将其转化为
。
ps: 为什么说对于约束函数 的理解不要单纯局限于变量呢,对于这里的约束条件来说,有的教程可能就会以
的形式出现,就相当于将
等同于
,其实将P挪过来,再将整体等同于
是一样的。
2.2.3 使用拉格朗日乘子法求解
1. 构造拉格朗日函数:引入拉格朗日乘子λ,构造拉格朗日函数

2. 求偏导数并令其为0:

3. 解方程组:由和
可知
,将其代入约束条件
中,得到
即。
2.3 拉格朗日函数的数学原理
在深度学习中有过拟合的情况,一般采用……的方法,那么这种方法在深度学习中的具体应用是什么样的呢?以及在什么条件下会满足呢?

相关内容在第一节有详细介绍
那么约束条件与目标函数的关系在图像中的体现是怎么样的呢?怎么通过图像来理解这个概念呢?
注意:目标函数是一个曲面,而约束条件是一条曲线,其实也是一条等高线,只不过高度为0(在xoy平面)。
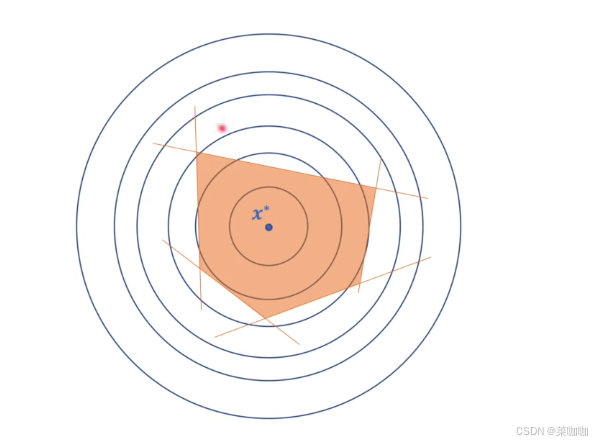
下图展示了一个目标函数等高线与约束条件的示意图:
那么拉格朗日函数的极值点在哪里呢?由于我们只能在约束条件的曲线上考虑目标函数的值,哪个点才是极值呢?明显对应于图中红色的那个点,但是有什么根据吗?
可以从以下两点考虑:
1.梯度,若想找到拉格朗日函数的极值点,那么极值点处的梯度必然为0,若想拉格朗日函数的梯度为0,那么目标函数和约束函数的梯度必须在一条直线上,因为梯度是标量,如果不在一条直线上,这两个函数的梯度相加必不可能等于0,因此目标函数和约束函数的等高线必相切。
2. 直观理解,如果极值点处不相切,那就肯定会有一个交点,设交点为A,那么从A出发沿着约束函数这条曲线往左和往右走,肯定会得到分别大于和小于A处目标函数数值的两个目标函数数值。那么A处肯定就不是极值点。

2.4 多个约束条件下的拉格朗日对偶函数
具体看如下例子:

要满足上面图片中的要求,就要满足以下条件:

下面这种情况就相当于所有的约束条件都是松弛的(因为最小值就在约束范围内,所有的都为0):
3. 拉格朗日对偶
拉格朗日乘数法有自己的优点,但是也有相应的问题,不能保证自己找出的点就是极值点就是最值,有可能是鞍点,比如下图这种情况:

但是最值只有1个。像这种极值点不止一个的问题称为非凸问题。
那么什么是凸问题,什么是非凸问题?什么是凸函数,什么是凹函数?
1. 凸问题:目标函数是凸函数/凹函数,也就是说只有一个极值。在凸函数上求最小值,在凹函数上求最大值,一般情况下我们习惯于求最小值,因此遇到凹函数先加一个负号变成凸函数然后来求最小值,如下图所示:


但是并不是所有问题都是凸问题,如果遇到了非凸问题该怎么办呢?这个时候就需要用到拉格朗日对偶函数了,对于拉格朗日对偶问题有如下定义:
3.1 拉格朗日原问题
假设 f ( x ) , c i ( x ) , h j ( x ) f(x),c_i(x),h_j(x) f(x),ci(x),hj(x)是定义在 R n R^n Rn上的连续可微函数,考虑约束最优化问题:

ps:很多人都在想为什么这么假设?这是一个通用性的假设,适用于所有情况!!!因为 他不就是
吗?然后你就把
重新理解为
不就完事了?有小于等于0,有大于等于0,还有等于0,这不就是适用于所有情况的一种假设吗?
将上述情况成为约束最优化问题的原始问题。
如果不考虑约束条件,原始问题就是:
![]()
因为假设其连续可微,利用高中的知识,f(x)求导数,然后令导数为0,就可解出最优解很简单。但是问题来了,这里有约束条件,必须想办法把约束条件去掉才行, 拉格朗日函数派上用场了。
利用上节介绍的拉格朗日函数来“去约束”:


网上很多资料都是将这个拉格朗日函数的计算分为两层,来实现对f(x)的等价求min,如下所示:
![]()
![]()
那么这种形式为什么能够在约束条件内的同时又求出min f(x)呢?
首先第一个式子是将x视为固定数值,也就是常量,求出 ,,此时 f(x) 相当于常量,那么此时α和β取什么数值会使得
取到最大值呢?这里有两种情况:
1. x 符合约束条件,此时,那么因为 α ≥ 0,因此
最大值为0,此时
,因为符合约束条件因此
,此时
。
2. x不符合约束条件,此时,那么因为 α ≥ 0,因此
最大值为
,此时
,此时
,很轻易能够得到使得
的
。
至此和
已经固定下来了,那么对于min来说,是将
和
视作常数,将x视作变量,此时会有如下情况:
1. 对于符合约束条件的x,由第一步已经推出,此时对其求最小值,就相当于对 f(x) 求最小值,这就等价于原问题了。
2. 对于不符合约束条件的x,由于其max为无穷大,,
,对其求min没有意义,因为值太大了,肯定不会选择这个x。所以就将其直接排除掉了。具体可以如下这么理解:
![]()
3.2 拉格朗日对偶问题
上面讲述的都是拉格朗日原问题,那么拉格朗日对偶问题是什么呢?看如下图示:

对偶问题的提出就是为了解决非凸问题,对偶问题有一个特性:不论原问题是什么,换成对偶问题都是一个凸问题。
为了更好地理解对偶问题,我们有一些概念需要了解,例如凸集、凸优化
3.2.1 凸集
所谓凸集就是在该集合内任意两点之间的连线,这条线上的所有点都在集合范围内,下图中,左边就是非凸集,右边是凸集。

3.2.1.1 仿射集
上面的图片中对有限制,就相当于是线段,当对
没限制的时候,就是一条直线,如果
、
是多维度的话,那就是一个超平面,这种集合称为仿射集,仿射集一定是凸集。

多个仿射集相交也一定是凸集
3.2.2.2 半空间
半空间也是凸集,多个半空间的交集也是凸集




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








