【CV】吴恩达机器学习课程笔记 | 第9章

本系列文章如果没有特殊说明，正文内容均解释的是文字上方的图片
机器学习 | Coursera
吴恩达机器学习系列课程_bilibili

9 神经网络：Learning

9-1 应用于神经网络的代价函数

• 用$L$表示神经网络的总层数（Layers）
• 用$s_l$表示第$l$层单元（神经元）的数量（不包括偏置单元）
• $h_{\Theta }(x)\in {\mathbb{R}}^K$（$h_{\Theta }(x)$为$K$维向量，即神经网络输出层共有$K$个神经元，即有$K$个输出）
• $(h_{\Theta }(x){)}_i=i^{th}output$（$(h_{\Theta }(x){)}_i$表示第$i$个输出）

应用于神经网络的代价函数为：

$$J(\Theta )=-\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}^{(i)}log(h_{\Theta }(x^{(i)}){)}_k+(1-y_k^{(i)})log(1-(h_{\Theta }(x^{(i)}){)}_k)\right]+\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}({\Theta }_{ji}^{(l)}{)}^2$$

• 第二项中的${\sum }_{i=1}^{s_l}{\sum }_{j=1}^{s_{l+1}}$指的是将$s_{l+1}$行$s_l$列的矩阵${\Theta }_{ji}^{(l)}$中的每一个元素相加起来
• 第二项中的${\sum }_{l=1}^{L-1}$指的是将输入层和隐藏层的矩阵都求和

9-2 反向传播算法

• ${\delta }_j^{(l)}$定义为第$l$层第$j$个神经元的偏差（“error”）
  
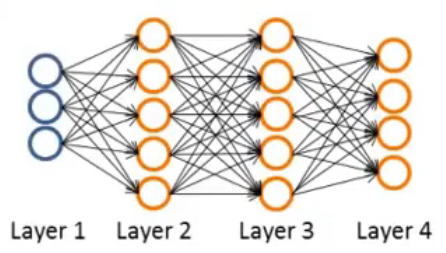
  以上图的四层的神经网络为例
• ${\delta }_j^{(4)}=a_j^{(4)}-y_j$（$y_j$指第$j$个输出在数据集中的值，$a_j^{(4)}$指神经网络的第$j$个输出，$a_j^{(4)}$也可表示为$(h_{\Theta }(x){)}_j$）
• 用向量方法表示上式可表示为${\delta }^{(4)}=a^{(4)}-y$，也可表示为${\delta }^{(4)}=h_{\Theta }(x)-y$
• ${\delta }^{(3)}=({\Theta }^{(3)}{)}^T{\delta }^{(4)}\cdot g^{\prime }(z^{(3)})$
  其中$g^{\prime }(z^{(3)})=a^{(3)}\cdot (1-a^{(3)})$
• ${\delta }^{(2)}=({\Theta }^{(2)}{)}^T{\delta }^{(3)}\cdot g^{\prime }(z^{(2)})$
  其中$g^{\prime }(z^{(2)})=a^{(2)}\cdot (1-a^{(2)})$

点乘结果是一个数，叉乘结果是一个向量

• $\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=a_j^{(l)}{\delta }_i^{(l+1)}$
  这里忽略了正则化项，即认为$\lambda =0$
  
• 上图是反向传播算法的流程，最后可以得到$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=D_{ij}^{(l)}$，然后进行梯度下降算法

9-3 理解反向传播

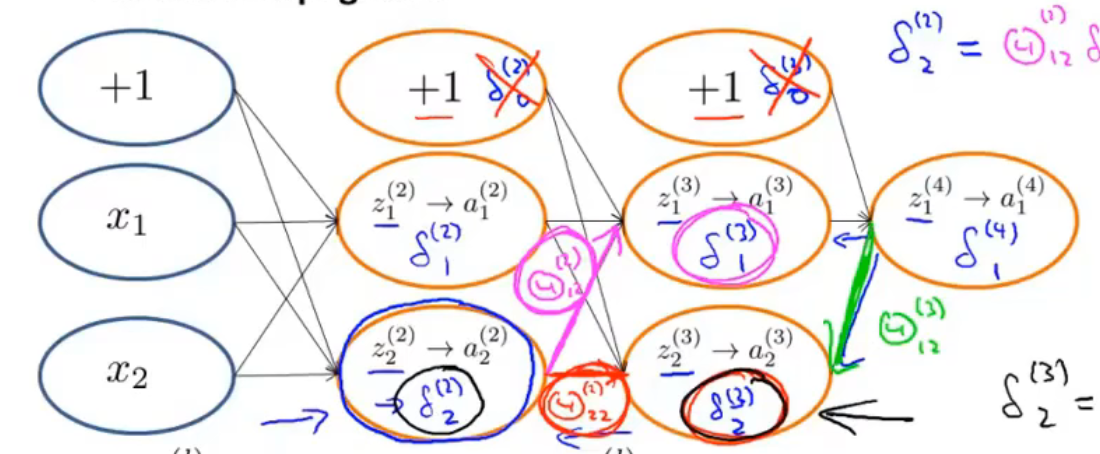
以上图的神经网络为例

• ${\delta }_2^{(2)}={\Theta }_{12}^{(2)}{\delta }_1^{(3)}+{\Theta }_{22}^{(2)}{\delta }_2^{(3)}$
• ${\delta }_2^{(3)}={\Theta }_{12}^{(3)}{\delta }_1^{(4)}$

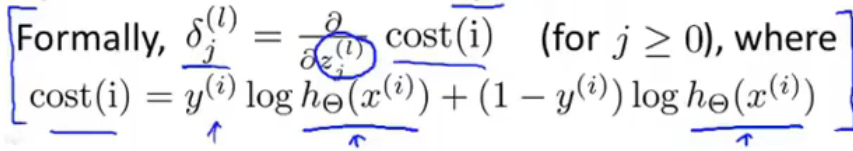
9-4 展开参数

9-5 梯度检测

要估计代价函数$J(\Theta )$上点$(\theta ,J(\Theta ))$处的导数值，可以运用$\frac{\mathrm{d}}{\mathrm{d}\theta }J(\theta )\approx \frac{J(\theta +\epsilon )-J(\theta -\epsilon )}{2\epsilon }(\epsilon =10^{-4}为宜)$求得导数

扩展到向量中，如上图

• $\theta$是一个$n$维向量，是矩阵${\Theta }^{(1)},{\Theta }^{(2)},{\Theta }^{(3)},...$的展开
• 可以估计$\frac{\partial }{\partial {\theta }_n}J(\theta )$的值

将估计得到的偏导数值与反向传播得到的偏导数值比较，如果两个值非常近，就可以验证计算是正确的
一旦确定反向传播算法计算出的值是正确的，就应该关掉梯度检验算法

9-6 随机初始化

如果在程序开始时令$\Theta$中所有元素均为0，会导致多个神经元计算相同的特征，导致冗余，这成为对称权重问题
所以在初始化时要令${\Theta }_{ij}^{(l)}$等于$[-ϵ,ϵ]$中的一个随机值

9-7 回顾总结

训练一个神经网络：
1.随机一个初始权重
2.执行前向传播算法，得到对所有$x^{(i)}$的$h_{\Theta }(x^{(i)})$
3.计算代价函数$J(\Theta )$
4.执行反向传播算法，计算$\frac{\partial }{\partial {\Theta }_{jk}^{(l)}}J(\Theta )$
(get $a^{(l)}$ and ${\delta }^{(l)}$ for $l=2,...,L$)
5.通过梯度检验算法得到估计的$J(\Theta )$的偏导数值，将估计得到的偏导数值与反向传播得到的偏导数值比较，如果两个值非常近，就可以验证反向传播算法的计算结果是正确的；验证完后，关闭梯段检验算法(disable gradient checking code)
6.运用梯度下降算法或其他更高级的优化方法，结合反向传播计算结果，得到使$J(\Theta )$最小时的参数$\Theta$的值