【CV】吴恩达机器学习课程笔记 | 第14章

本系列文章如果没有特殊说明，正文内容均解释的是文字上方的图片
机器学习 | Coursera
吴恩达机器学习系列课程_bilibili

14 降维

14-1 目标I：数据压缩

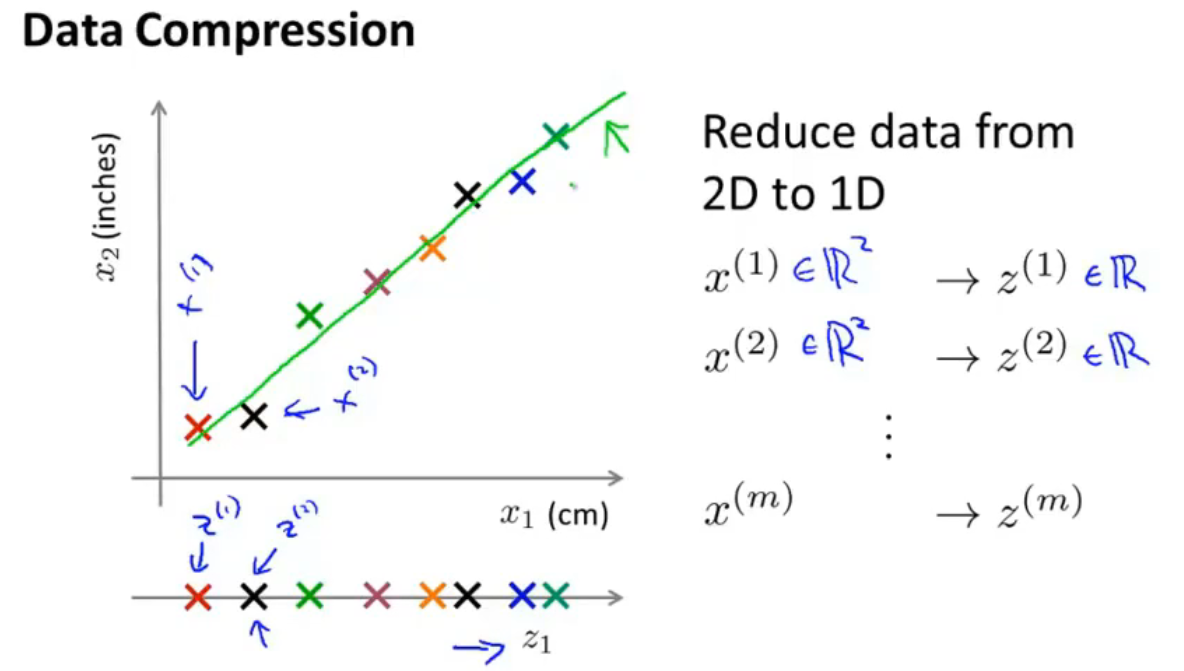
如上图，将数据从二维压缩为一维，以表示同一个物体的长度为例，$x_1$为用厘米表示，$x_2$为用英尺表示，由于四舍五入产生的误差，坐标系中的样本坐标没有完全练成一条直线，对其进行线性拟合，得到一条直线，让这些点投影在另一条坐标轴$z$上，这样，可以用一个一维的数字$z^{(i)}$来表示原来的一个二维向量$x^{(i)}$

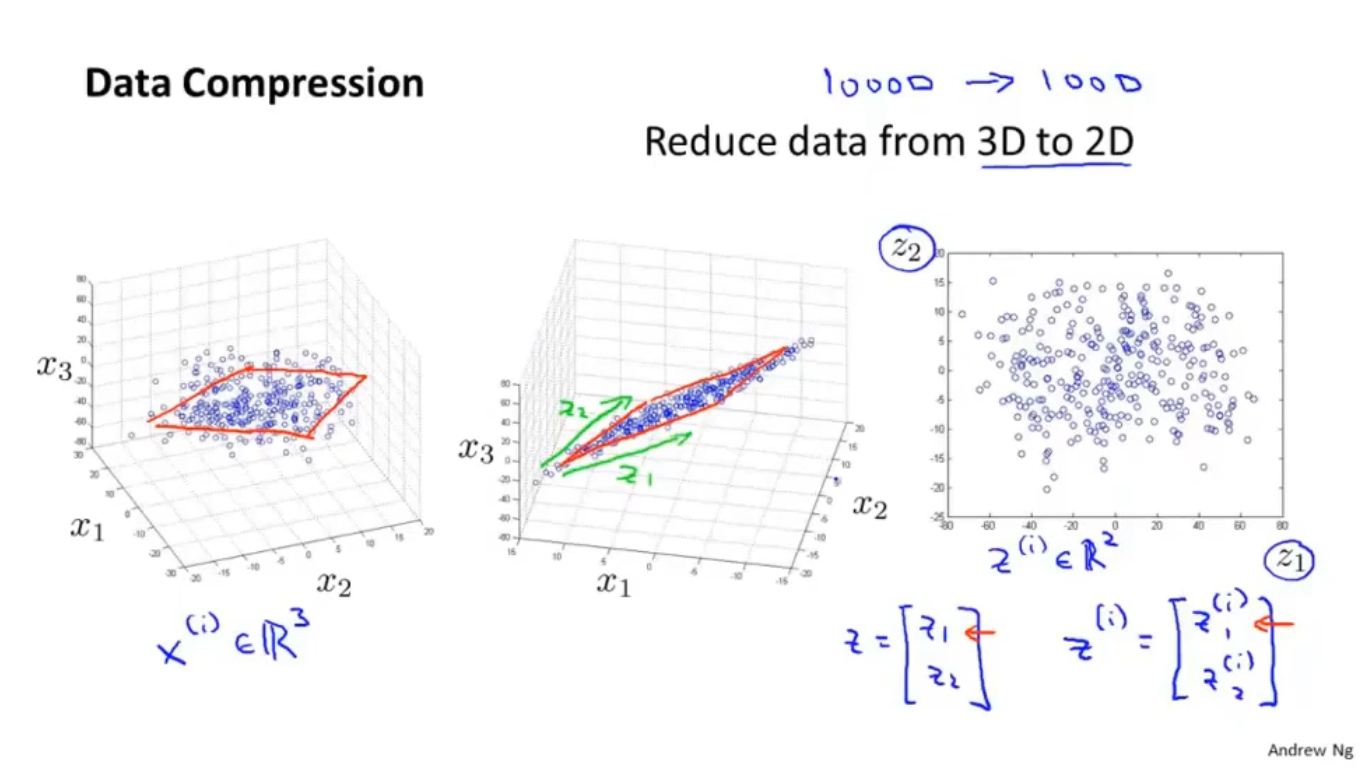
如上图，将数据从三维压缩为二维，（在实际应用中可能是将10000维的数据压缩为1000维），空间中所有的点几乎都在一个平面的周围，将所有的点投射到这个平面上，用$z_1$和$z_2$来表示平面的两个坐标轴，这样就把一个三维空间压缩为二维平面，原来的数据用一个二维向量$z^{(i)}$即可表示，$z^{(i)}$中有两个特征$z_1^{(i)}$和$z_2^{(i)}$

降维后的数据可以提高学习算法的运算效率并且节省磁盘存储空间

14-2 目标II：可视化

一般取k=2 or k=3来可视化数据集

14-3 主成分分析方法（PCA）

有这样的一个数据集，这个数据集含有二维实数空间内的样本，假设我想对数据进行降维，从二维降到一维，也就是说，我需要找到 一条直线，将数据投影到这条直线上
上图中红线是一个不错的选择，因为每个点投影到直线上的距离（蓝线）都很短
所以，PCA就是寻找一个低维的东西（在这个例子中是一条直线），让数据投射在上面时的距离的平和最小，这个距离被称为投影误差
在使用PCA钱，需要先进行均值归一化和特征规范化，使得特征$x_1$和$x_2$均值为0，数值在可比较的范围之内

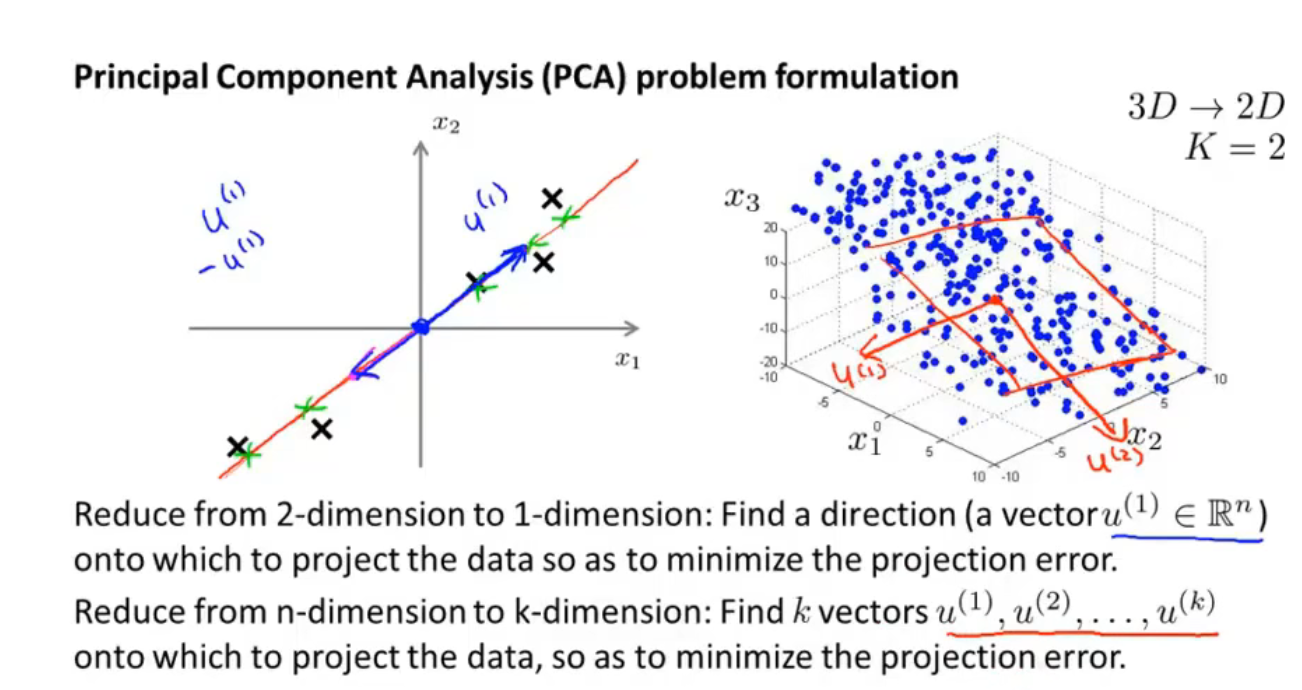
由二维到一维时，找到一个向量即可，三维到二维时，需要找到2个向量组成一个平面，更高维时，需要找到k个向量，让样本投影到这k个向量展开的线性子空间上

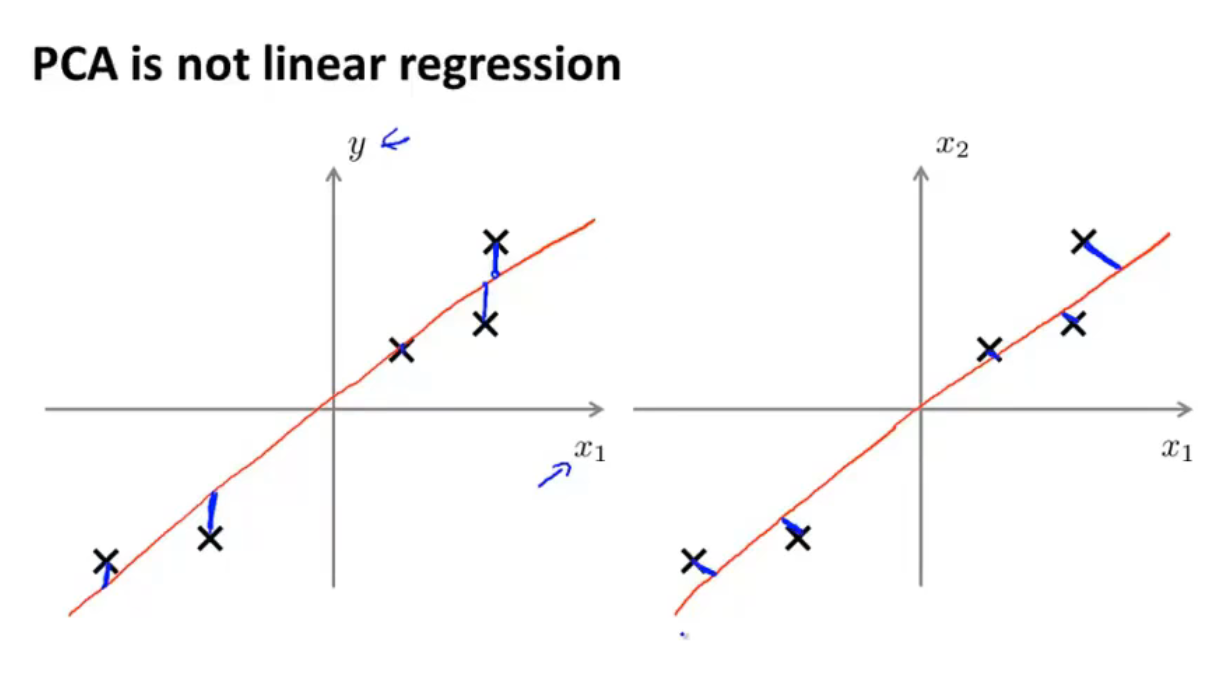
上图解释了PCA与线性回归的不同：

• 线性回归是左侧的坐标系，他对一条条竖直的（与y轴平行的）蓝线求和，因为线性回归计算出的误差是指预测的y值与实际y值之间的差
• PCA是右侧的坐标系，他对一条条垂直于降维后的直线（在这里是直线）的蓝线求和，因为PCA计算的是实际的点与降维后直线的距离，实际的点是投影上去的

14-4 主成分分析算法（PCA）

首先进行数据预处理，进行均值标准化，可能要进行特征缩放
均值标准化：

• 按照上图先求出某个特征在所有样本中的平均值${\mu }_j$，公式为${\mu }_j=\frac{1}{m}{\sum }_{i=1}^m{x}_j^{(i)}$
• 然后把每一个旧的$x_j^{(i)}$替换成$x_j-{\mu }_j$，这样每一个特征的均值都为0
  
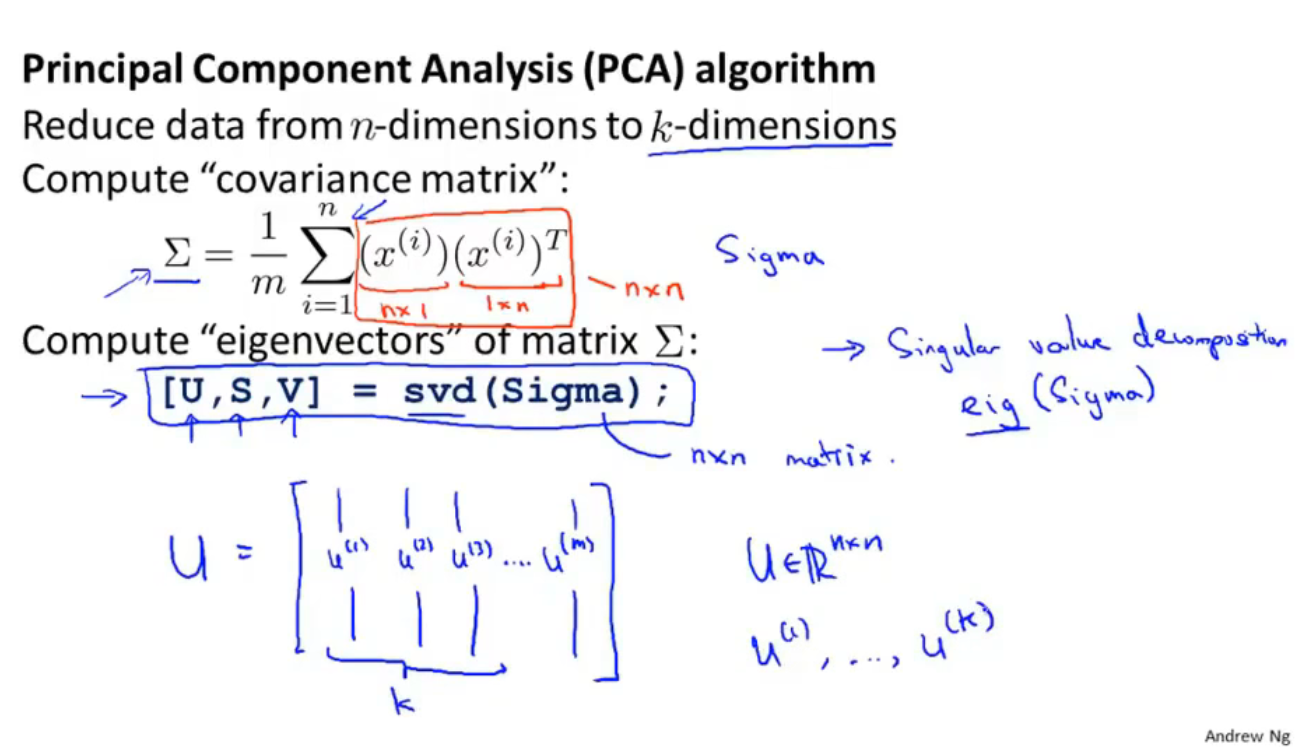
  先计算$\Sigma$矩阵（协方差），计算公式为：$\Sigma =\frac{1}{m}{\sum }_{i=1}^n\left(x^{(i)}\right){\left(x^{(i)}\right)}^T$，表示为矩阵形式为$\Sigma =\frac{1}{m}{X}^{T}X$
  然后用软件库调用svd算法得到矩阵$U$，$U$是一个n×n的矩阵，这里的n=m，因为共有n=m个样本数量，取矩阵$U$的前k列就是要降维成的k维空间里的k个向量（空间是几维就需要几个向量来表示这个空间，如三维降二维时需要两个向量来表示二维空间）
  
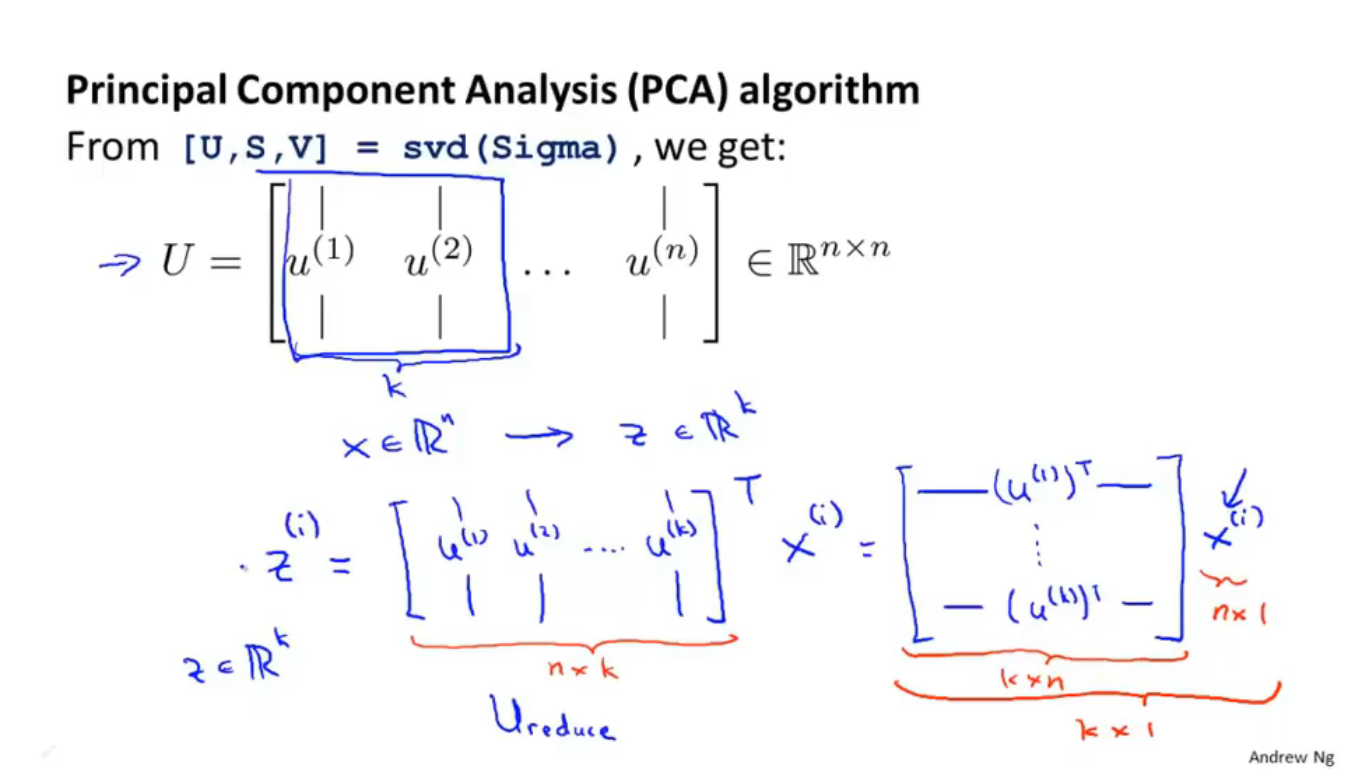
  如上图，把刚刚取出的k个列向量组成的矩阵命名为$U_{reduce}$，则得到的低维（k维）的数据集$z^{(i)}=U_{reduce}^T{x}^{(i)}$，该数据集是一个k维向量

14-5 压缩重现（解压缩）

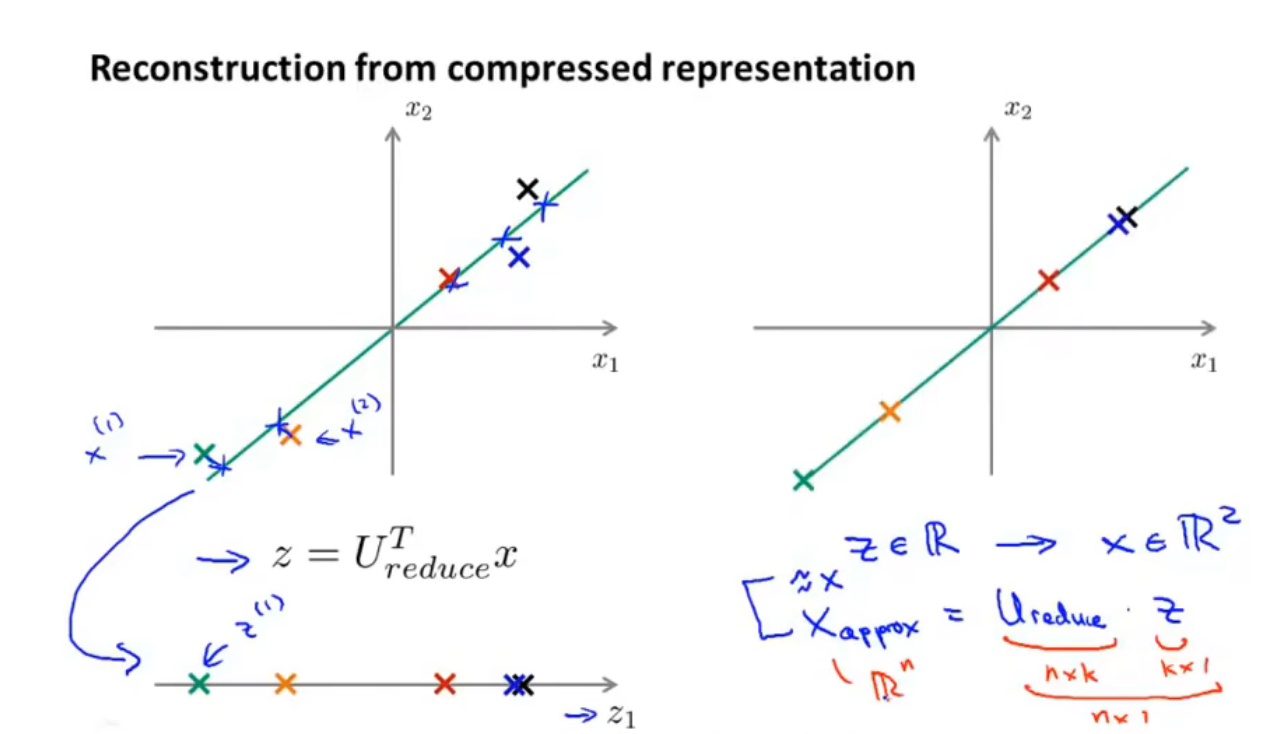
之前进行了这样的运算：$z=U_{reduce}^{T}x$
其中$z$是新得到的一维向量，$x$是原来的二维向量，$U_{reduce}^T$是通过svd算法得出的
现在要恢复二维，进行这样的运算：$x_{appox}=U_{reduee}z$

14-6 选择主成分数量

上图中分子的式子称为平均平方映射误差，分母称为数据的总变差（它的意思是 “平均来看 我的训练样本 距离零向量多远？ 平均来看 我的训练样本距离原点多远？），分数计算的结果为降维后的新数据与原数据的差距有多大
比如假设结果$\le 0.01$，则可以说有1%的差异，这个数字比较典型的取值为0.01、0.05、0.10甚至也可能是0.15
上图左侧是计算合适的k值的方法，这里假设与原数据有小于等于1%的误差
可以直接调用svd算法，其中输出的$S$矩阵是一个对角阵
用公式$1-\frac{{\sum }_{i=1}^k{s}_{ii}}{{\sum }_{i=1}^n{s}_{ii}}⩽0.01$，直接判断这个公式是否成立即可，找到让这个公式成立的k的值就是合适的k的取值，或者用$\frac{{\sum }_{i=1}^k{s}_{ii}}{{\sum }_{i=1}^n{s}_{ii}}⩾0.99$来判断也是一样的

• 即使要手动选择k值，计算出差异值也可以帮助向别人解释你实现的 PCA 的性能 的一个好方法 ，熟悉 PCA 的人们 就可以通过它 来更好地理解 你用来代表原始数据的 100维数据 近似得有多好 因为有99%的差异性被保留了

14-7 应用PCA的建议

在使用监督学习时，也可以运用PCA来增加运算效率

• 先将$x^{(1)},x^{(2)},\dots ,x^{(m)}$从原来的样本中抽出，运用PCA算法将其降维得到$z^{(1)},z^{(2)},\dots ,z^{(m)}$，然后把降维后的$z^{(1)},z^{(2)},\dots ,z^{(m)}$替换到原来的样本中，与y一一对应，然后进行监督学习的算法
• 注意：PCA只能在训练集中使用，不能用于交叉验证集和测试集，从训练集得到了$x$到$z$的对应关系后，可将这个对应关系应用到交叉验证集和测试集

• 不要用PCA来防止过拟合，更好的方法是用正则化
• PCA是在丢失一定精度的境况下提高运算效率，它在降维时没有与y相关
• 在使用PCA之前首先尝试使用原数据进行运算，只有在运算速度过慢、占用内存太大、占用磁盘太大、原数据无法成功计算时才使用PCA