Codeforces Round #554 (Div. 2) C. Neko does Maths（gcd好题）

最新推荐文章于 2023-01-21 12:44:14 发布

原创最新推荐文章于 2023-01-21 12:44:14 发布 · 170 阅读

0 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

28 篇文章

订阅专栏

本文探讨了如何找到最小的k值，使得a+k和b+k的最小公倍数达到最小。通过枚举b-a的因子，寻找最优解，利用__gcd函数进行计算。适用于数学算法竞赛和计算机科学领域的最小公倍数问题。

题目链接
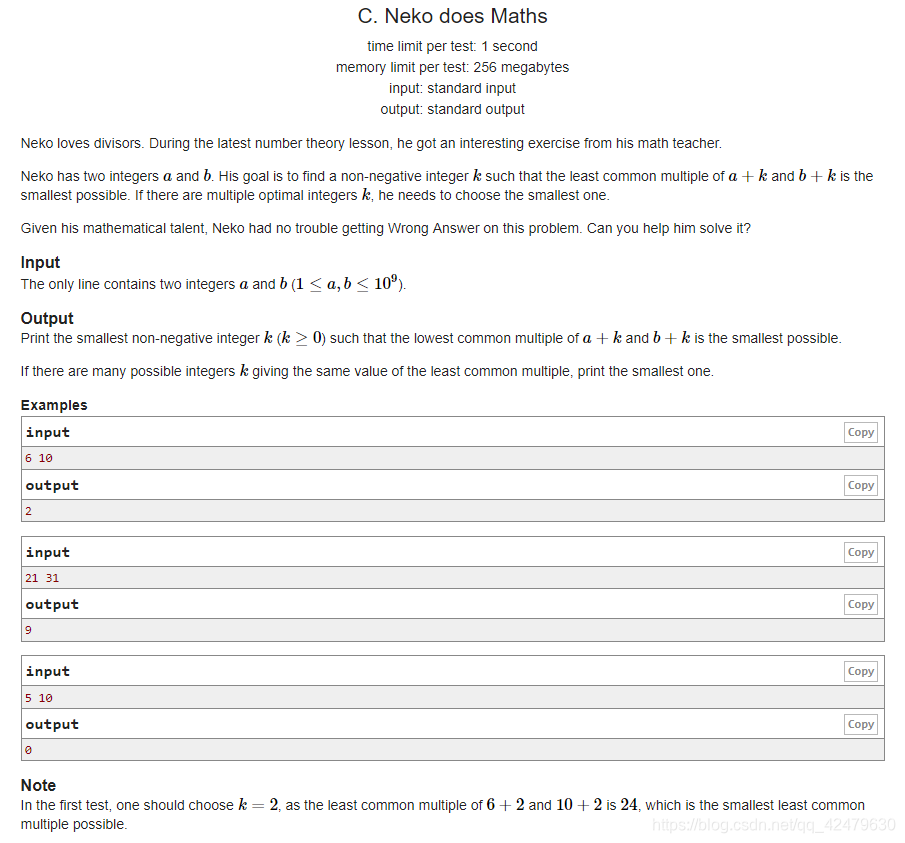
在这里插入图片描述
题意：给出a和b，求最小的k使得a+k和b+k的最小公倍数最小。
思路：一开始想化简式子，结果方向就走错了。。。这里有个gcd的性质gcd（a，b-a），所以gcd（a+k，b+k）=gcd（a+k，b-a）最终的答案就是（a+k）*（b-a）/gcd（a+k，b-a），怎么样才能使它最小呢，如果分子分母能够化简肯定是可以减小的，所以a+k和b-a一定要存在因子可以消，因为b-a是固定的所以我们只要枚举b-a的因子，最小值一定在这里面，暴力比较就可以了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll; 
vector<ll>v;
int main()
{
	ll a,b;
	scanf("%lld%lld",&a,&b);
	if(a>b) swap(a,b);
	for(ll i=1;i*i<=b-a;++i)
	{
		if((b-a)%i==0) v.push_back((b-a)/i),v.push_back(i);
	}
	ll ans=1e18,k;
	for(int i=0;i<v.size();++i)
	{
		ll t=0;
		if(a%v[i]!=0) t=v[i]-a%v[i];
		ll temp=(a+t)*(b+t)/__gcd(a+t,b+t);
		if(ans>temp) ans=temp,k=t;
	}
	if(a==b) k=0;
	printf("%lld\n",k);
}