矩阵的低秩逼近以及逼近后的误差计算——matlab实现

一.矩阵的低秩逼近

1.1 低秩矩阵的创建

$A$为$m\times n$大小的矩阵，则$svd$分解以后$[USV]=svd(A)$里面，$U$为$m\times m$，$S$为$m\times n$，$V$为$n\times n$

A = randn(8,8);%首先随机创建一个8×8的矩阵
[U S V] = svd(A);%对矩阵进行svd分解

%低秩矩阵逼近的构建
k = 5;%选择秩为k去逼近A（注意：此时A的秩最多为8）
Ak = U(:,1:k)*S(1:k,1:k)*V(:,1:k)';%k=5，表明使用秩5逼近原矩阵

1.2 秩1矩阵

1.1表述的低秩逼近写的是用秩为k的矩阵去逼近原矩阵A。
但是其实可以在细分一点。矩阵A其实可以拆解成全部秩为1的矩阵相加得到。公式如下：
$A={\sum }_{i=1}^k{\delta }_i{p}_i{q}_i^T={\delta }_1{p}_1{q}_1^T+{\delta }_2{p}_2{q}_2^T+...+{\delta }_k{p}_k{q}_k^T$

其中$p_i$为左奇异矩阵$U$里面的列向量，${\delta }_i$为S里面的奇异值，$q_i$为右奇异矩阵的列向量。

例如：
用1.1去构建的秩2矩阵
k = 2;%选择秩为2去逼近A（此时拿了前两个奇异值去构建的逼近矩阵）
Ak = U(:,1:k)*S(1:k,1:k)*V(:,1:k)';%k=5，表明使用秩2逼近原矩阵
用1.2去构建的两个秩1矩阵
${\delta }_1{p}_1{q}_1^T$和${\delta }_2{p}_2{q}_2^T$
两者关系
Ak=${\delta }_1{p}_1{q}_1^T+{\delta }_2{p}_2{q}_2^T$

二.逼近的矩阵与原矩阵的误差计算

2.1 常规的矩阵与原矩阵的误差计算

norm(A-Ak) ;%1.2的秩1矩阵就拿这个来算即可

2.2 理论直接看出

有一个theorem ，指出一个矩阵A及其秩k近似的矩阵Ak之间的误差具有由A的第k+1个奇异值给定的。

三.example

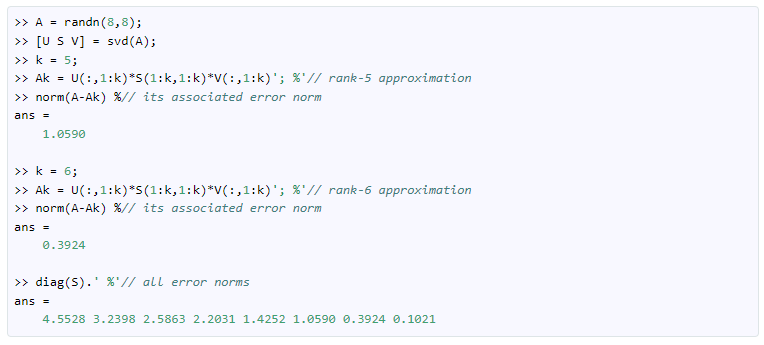
参考资料：http://www.uwenku.com/question/p-rfkumipp-zt.html
侵权请联系