基于CAD二次开发的道路纵断面竖曲线计算原理与编程自动绘制方法（以C#为例）

针对道路纵断面竖曲线绘制（二次抛物线）问题，本文将先举个例题进行说明【不熟悉最好手算验证】，之后在对其编程思路进行简述，最后将附上各部分代码供参考交流学习。OK，开始进入正题。

---

目录

1.基本原理

2. 编程实现

 3.总结：

---

1.基本原理

 

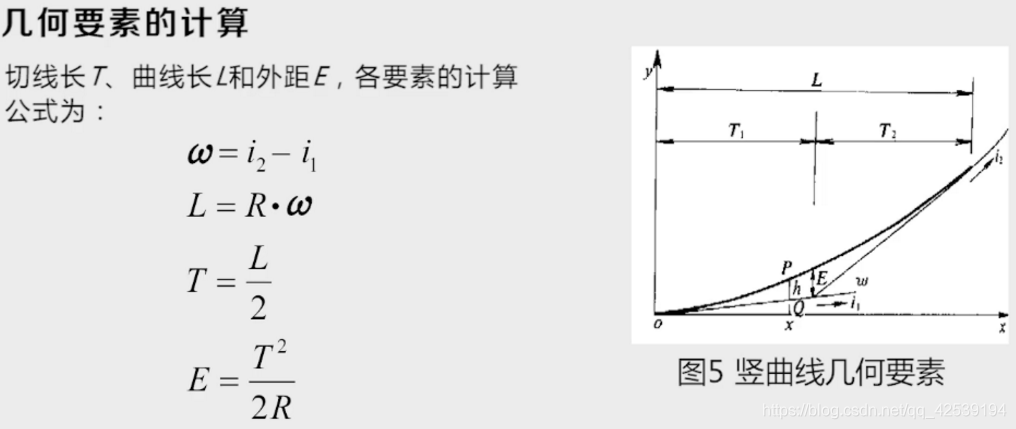
 解：

1)

 因为大于0，所以他是凹曲线。

2）

 3）

起点里程=边坡点里程-T=k25+460-105=k25+355

终点里程=边坡点里程+T=k25+460+105=k25+565

起点只边坡点的高程改正：

y1=i1*T=0.8%*105=0.84m

起点高程：

H起=H变坡-y1=780.72-0.84=779.88

边坡点至终点的高程改正数：

y2=i2*T=5%*105=5.25m

终点高程：

H终=H变+y2=780.72+5.25=785.97m

注意：高程改正数不用添加绝对值，因为坡度正负不一样，直接影响了高程改正数的正负不一样。在编程计算过程中求起点高程直接用变坡高程-改正数，求终点高程直接用变坡高程+改正数即可，不用考虑是凹曲线还是凸曲线。

至此起点和终点的高程和桩号都已计算完毕。

 那么接下来就开始分别计算其设计高程：

竖距：

k25+400距起点平距为：45m

H任意点=H起+H切+h【注意符号：h>0时，凹的时候返回+h，凸的时候返回-h】

 

k25+460距起点平距为：105m

 

k25+500距起点平距为：145m

H3=779.88+0.8%*145=781.04m

y3=145*145/2*5000=2.1025m

HD3=781.04+2.1025=783.1425m

2. 编程实现

 定义一个单独的竖曲线类库VertiCurve存放每一条竖曲线数据：本次实例有17个边坡点，因此有16个坡，15个竖曲线。两端的不算。

 public class VertiCurve
    {
        /// <summary>
        /// 坡度差
        /// </summary>
        public double w { get; set; }
        /// <summary>
        /// 竖曲线长度
        /// </summary>
        public double  L { get; set; }
        /// <summary>
        /// 竖曲线半径
        /// </summary>
        public double R { get; set; }
        /// <summary>
        /// 竖曲线切线长
        /// </summary>
        public double T { get; set; }
        /// <summary>
        /// 竖曲线外距
        /// </summary>
        public double E { get; set; }
        /// <summary>
        /// 起点桩号
        /// </summary>
        public double StationStart { get; set; }
        /// <summary>
        /// 终点桩号
        /// </summary>
        public double StationEnd { get; set; }
        /// <summary>
        /// 起点高程
        /// </summary>
        public double HeightStart { get; set; }
        /// <summary>
        /// 终点高程
        /// </summary>
        public double HeightEnd { get; set; }
        /// <summary>
        /// 边坡点桩号
        /// </summary>
        public double stationBpd { get; set; }
        /// <summary>
        /// 起始坡度
        /// </summary>
        public double  i1 { get; set; }

    }

定义一个集合专门存放17个边坡点，边坡点属性有编号id、高程Height、桩号Station以及曲率半径Radius，

    public class MyPointZDM
    {
        //序号
        public int Id { get; set; }
        //高程
        public double Height { get; set; }
        //桩号
        public double Station { get; set; }
        //半径
        public double Radius { get; set; }
    }

//定义纵断面桩号和高程（点）和半径的集合
   List<MyPointZDM> objMyPointRadiusList = new List<MyPointZDM>();

 根据17个边坡点将15个竖曲线全部找到并存入竖曲线集合：

 //定义一个竖曲线集合
 List<VertiCurve> VertiCurveList = new List<VertiCurve>();

        //获取所有竖曲线【输入：纵断面数据】
        public void GetAllVertiCurve(List<MyPointZDM> objMyPointRadiusList)
        {
            for (int i = 1; i < objMyPointRadiusList.Count-1; i++)
            {
                double i1 = (objMyPointRadiusList[i].Height - objMyPointRadiusList[i - 1].Height)/(objMyPointRadiusList[i].Station-objMyPointRadiusList[i-1].Station);
                double i2 = (objMyPointRadiusList[i+1].Height-objMyPointRadiusList[i].Height) / (objMyPointRadiusList[i+1].Station-objMyPointRadiusList[i].Station);
                double w = i2 - i1;
                double R = objMyPointRadiusList[i].Radius;
                VertiCurve objCur = new VertiCurve();
                objCur.stationBpd = objMyPointRadiusList[i].Station;
                objCur.w = w;
                objCur.L = Math.Abs( w) * R;
                objCur.T = objCur.L / 2;
                objCur.E =Math.Pow(objCur.T,2)/2*R;
                objCur.R = R;
                objCur.i1 = i1;
                objCur.StationStart = objCur.stationBpd - objCur.T;
                objCur.StationEnd = objCur.stationBpd + objCur.T;
                //起点到变坡点高程改正数
                double v1 = objCur.T * i1;
                objCur.HeightStart = objMyPointRadiusList[i].Height - v1;
                double v2 = objCur.T * i2;
                objCur.HeightEnd = objMyPointRadiusList[i].Height + v2;
                VertiCurveList.Add(objCur);
            }
        }

 随后开始绘图测试：

思路说明：在起点终点之间并不是直接绘制Arc曲线，而是将起点和终点的距离微分成若干部分，step就是每一部分的长度，随后计算每一部分的终点坐标，这样一段一段的绘制polyline多段线，就可以形成一个曲线，这么做的好处就是可以自定义步长，并且未来可以进行比例缩放。

 db.DrawGraph(pl);是我对database类写的扩展方法，意思就是传入一个entity，就将其展示到图形上：

 private void btnBeta_Click(object sender, EventArgs e)
        {

            GetAllVertiCurve(objMyPointRadiusList);
            Database db = new Database();
            //根据间隔步长绘制多段线，便于压缩
            int step = 1;
            for (int i = 0; i < VertiCurveList.Count; i++)
            {
                double xs = VertiCurveList[i].StationStart;
                double ys = VertiCurveList[i].HeightStart;
                double xe = VertiCurveList[i].StationEnd;
                double ye = VertiCurveList[i].HeightEnd;
                Polyline pl = new Polyline();
                double stationCurrent = VertiCurveList[i].StationStart; 
                while (stationCurrent <= xe)
                {
                    int index = 0;
                    double x = stationCurrent - xs;
                    //凹的时候返回+h凸的时候返回-h
                    double h = (VertiCurveList[i].w > 0 ? 1 : -1)*Math.Pow(x, 2) / (2 * VertiCurveList[i].R);
                    double yNew = ys + (stationCurrent - VertiCurveList[i].StationStart) * VertiCurveList[i].i1 + h;
                    Point2d p = new Point2d(stationCurrent/10, yNew);
                    pl.AddVertexAt(index, p, 0, 0, 0);
                    index++;
                    stationCurrent += step;
                }
                db.DrawGraph(pl);
            }

        }

 3.总结：

绘制竖曲线纵断面思路很清晰，理论上不存在难点，但是鄙人不才，绘制的总是不对，研究了很久在发现是竖锯和对应点位切线高程符号的问题，上面我已己经将容易出问题的地方红色标注了。最后欢迎大家留下宝贵的意见。