机器学习 --- 支持向量机（Support Vector Machine）推导+实例

支持向量机（Support Vector Machine）

支持向量机要解决的问题

• 要解决的问题：什么样的决策边界才是最好的呢？

以一个二分类问题为例，对于两个类别，可以有多种决策边界，需要找到一个最好的那个决策边界

• 特征数据本身如果就很难分，怎么办呢？

使用核函数

• 计算复杂度怎么样？能实际应用吗？

• 目标：基于上述问题对SVM进行推导

决策边界：
需要选出来Large Margin，就是说希望两条边界能够越宽越好

距离与数据定义

距离的计算：
边界是由两类的靠近决策边界的点来决定的

首先定义一个超平面 $w^T+b=0$

我们要对一个点到一个平面的计算，直接算垂直距离是比较困难的，借助其他方法求解：假设平面上有两个点 $x^{\prime }$、$x^{\prime \prime }$

①
$$w^T{x}^{\prime }=-b,w^T{x}^{\prime \prime }=-b$$

②
$$w\perp hyperplane:w^T\ast (x^{\prime \prime }-x^{\prime })$$

③
$$distance=project(x-x^{\prime })to\perp hyperplane$$

计算 $x-x^{\prime }$ 在垂直方向上的投影来求得距离：
$$distance(x,b,w)=|\frac{w^T}{||w||}(x-x^{\prime })|\stackrel{①}{\to }|\frac{1}{||w||}(w^{T}x+b)|$$

数据标签定义

数据集：$(X_1,Y_1)(X_2,Y_2)\dots (X_n,Y_n)$

$Y$ 为样本的类别： 当 $X$ 为正例时候 $Y=+1$ 当 $X$ 为负例时候 $Y=-1$

决策边界方程（注：在线性支持向量机中，$\varphi (x)$ 可看作 $x$）：
$$y(x)=w^T\varphi (x)+b$$

假设目标：
$$\Rightarrow \begin{array}{c}y(x_i)>0\iff y_i=+1\\ y(x_i)<0\iff y_i=-1\end{array}\Rightarrow y_i\cdot y(x_i)>0$$

优化的目标

通俗解释：找到一个条线$(w、b)$，使得离该线最近的点（雷区）
能够最远

因为 $y_i\cdot y(x_i)>0$ ，所以可以将点到直线的距离化简得：
$$|\frac{1}{||w||}(w^{T}x+b)|\Rightarrow \frac{y_i\cdot (w^T\varphi (x)+b)}{||w||}$$

目标函数

放缩变换：对于决策方程$(w、b)$可以通过放缩使得其结果值
$$|Y|\ge 1\Rightarrow y_i\cdot (w^T\varphi (x)+b)\ge 1$$

优化目标：
$$\underset{w,b}{\mathrm{argmax}}\left\{\begin{array}{c}\frac{1}{||w||}\underset{i}{\min }[y_i\cdot (w^T\varphi (x)+b)]\end{array}\right\}$$

由于 $y_i\cdot (w^T\varphi (x)+b)\ge 1$，那么$\underset{i}{\min }[y_i\cdot (w^T\varphi (x)+b)]=1$，得到 $\underset{w,b}{\mathrm{argmax}}\frac{1}{||w||}$，至此，目标函数搞定

目标函数求解

当前目标：
$$\underset{w,b}{\max }\frac{1}{||w||}$$

约束条件（前期假设）：
$$y_i\cdot (w^T\varphi (x)+b)\ge 1$$

根据当前的目标公式，是求 $\frac{1}{||w||}$ 的极大值，也就是求 $||w||$ 的极小值，那么这里就可以将求解极大值问题转换成极小值问题 $\Rightarrow \underset{w,b}{\min }\frac{1}{2}{w}^2$（引入常数和平方项，方便计算，且对最终解无影响）

使用应用拉格朗日乘子法求解：
$$L(w,b,\alpha )=f_0(x)-\sum _{i=1}^n{\alpha }_i(y_i(w^T\varphi (x)+b)-1)$$

SVM求解

分别对 $w$ 和 $b$ 求偏导,由于对偶性质，分别得到两个条件
$$\underset{w,b}{\min }\underset{\alpha }{\max }(w,b,\alpha )\to \underset{\alpha }{\max }\underset{w,b}{\min }(w,b,\alpha )$$
对 $w$ 求偏导：
$$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x)$$

对 $b$ 求偏导：
$$\frac{\partial L}{\partial b}=0\Rightarrow 0=\sum _{i=1}^n{\alpha }_i{y}_i$$

求导结果代入原式：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^n{\alpha }_i(y_i(w^T\varphi (x)+b)-1)$$

其中$w={\sum }_{i=1}^n{\alpha }_i{y}_i\varphi (x)$，$0={\sum }_{i=1}^n{\alpha }_i{y}_i$：

$$\begin{array}{rl}原式& =\frac{1}{2}{w}^{T}w-w^T\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x)-b\sum _{i=1}^n{\alpha }_i{y}_i+\sum _{i=1}^n{\alpha }_i\\ & =\sum _{i=1}^n{\alpha }_i-\frac{1}{2}(\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x){)}^T\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x)\\ & =\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}n{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)\end{array}$$

得到结果，继续进行对 $\alpha$ 求极大值，约束条件：${\sum }_{i=1}^n{\alpha }_i{y}_i=0$，${\alpha }_i\ge 0$
$$\underset{\alpha }{\max }(\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}n{\alpha }_i{\alpha }_j{y}_i{y}_j(\varphi (x_i{)}^T\cdot \varphi (x_j)))$$

引入负号，使得求极大值转化为求极小值，约束条件不变：
$$\underset{\alpha }{\min }(\frac{1}{2}\sum _{i=1,j=1}n{\alpha }_i{\alpha }_j{y}_i{y}_j(\varphi (x_i{)}^T\cdot \varphi (x_j))-\sum _{i=1}^n{\alpha }_i)$$

至此，再对 $\alpha$ 进行求解，得到结果后代入 $w={\sum }_{i=1}^n{\alpha }_i{y}_i\varphi (x)$ 得到最终 $w$

SVM求解实例

假设有一组包含三个点的数据，其中正例 $X_1(3,3)$ ，$X_2(4,3)$ ，负例$X_3(1,1)$

求解：
$$\frac{1}{2}\sum _{i=1,j=1}n{\alpha }_i{\alpha }_j{y}_i{y}_j(\varphi (x_i{)}^T\cdot \varphi (x_j))-\sum _{i=1}^n{\alpha }_i$$

约束条件：
$$\{\begin{array}{c}{\alpha }_1+{\alpha }_2-{\alpha }_3=0\\ {\alpha }_i\ge 0,i=1,2,3\end{array}$$

将数据代入：
$$原式=\frac{1}{2}(18{\alpha }_1^2+25{\alpha }_2^2+42{\alpha }_1{\alpha }_2-12{\alpha }_1{\alpha }_3-14{\alpha }_2{\alpha }_3)-{\alpha }_1-{\alpha }_2-{\alpha }_3$$

由于 ${\alpha }_1+{\alpha }_2-{\alpha }_3=0$，化简可得：
$$4{\alpha }_1^2+\frac{13}{2}{\alpha }_2^2+10{\alpha }_1{\alpha }_2-2{\alpha }_1-2{\alpha }_2$$

分别对 ${\alpha }_1$ 和 ${\alpha }_2$ 求偏导，偏导等于 $0$ 可得:$\begin{array}{c}{\alpha }_1=1.5\\ {\alpha }_2=-1\end{array}$

得到的结果并不满足约束条件 ${\alpha }_i\ge 0,i=1,2,3$，所以解应该在边界上
$$\begin{array}{rl}\begin{array}{c}{\alpha }_1=0\\ {\alpha }_2=-\frac{2}{13}\end{array}\Rightarrow 代入原式& =-0.153（不满足约束）\\ \begin{array}{c}{\alpha }_1=0.25\\ {\alpha }_2=0\end{array}\Rightarrow 代入原式& =-0.25（满足约束）\end{array}$$
所以，最小值在 $(0.25,0,0.25)$ 处取得

将 $\alpha$ 结果带入求解得：$\begin{array}{rl}w& =(0.5,0.5)\\ b& =-2\end{array}$

最终得到平面方程为：$0.5x_1+0.5x_2-2=0$

软间隔（soft-margin）

软间隔：有时候数据中有一些噪音点，如果将它们也考虑进去，那我们的两条决策边界就会变窄，达不到我们想要的效果

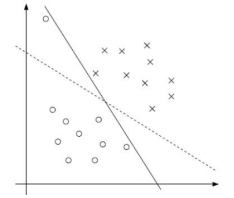
我们之前的方法要求要把两类点完全分得开，这个要求有点过于严格了，对于以上问题没有很好的考虑进去，那么为了解决这类问题，我们使用了以下方法：

引入松弛因子：
$$y_i(w\cdot x_i+b)\ge 1-{\xi }_i$$
新的目标函数：
$$min\frac{1}{2}||w|{|}^2+C\sum _{i=1}^n{\xi }_i$$
这里引入了一个新的控制变量 $C$，$C$是 ${\sum }_{i=1}^n{\xi }_i$ 的权重，$C$ 是我们需要指定的一个参数:

当 $C$ 趋近于很大时：意味着分类严格不能有错误
当 $C$ 趋近于很小时：意味着可以有更大的错误容忍

使用应用拉格朗日乘子法求解：
$$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^n{\xi }_i-\sum _{i=1}^n{\alpha }_i(y_i(w\cdot x_i+b)-1+{\xi }_i)-\sum _{i=1}^n{\mu }_i{\xi }_i$$
对各个参数求偏导：
$$\begin{array}{rlr}& w=\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x_n)& \\ & 0=\sum _{i=1}^n{\alpha }_i{y}_i& \\ & C-{\alpha }_i-{\mu }_i=0& \\ & {\alpha }_i\ge 0,{\mu }_i\ge 0& \end{array}$$

与线性支持向量机同样的解法：
$$\underset{\alpha }{\min }(\frac{1}{2}\sum _{i=1}^n\sum _{j=1}n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot y_i)-\sum _{i=1}^n{\alpha }_i)$$

得：
$$\begin{gathered} \sum _{i=1}^n{\alpha }_i{y}_i=0 \\ 0\le \alpha \le C \end{gathered}$$

SVM核变换

当一个分类数据在低维不可分时，可以映射到高维再进行分类

目标：找到一种变换的方法，也就是上面提到的 $\varphi (x)$

问题：核变换完成后，数据真的到了一个高维空间进行计算了吗？

例子：假设我们有两个数据，$x=(x_1,x_2,x_3),y=(y_1,y_2,y_3)$，此时在三维空间中已经不能对其进行划分，需要通过一个函数将数据映射到更高维的空间进行计算。比如映射到九维空间，函数为 $f(x)=x^2$，那么 $f(x)=(x_1{x}_1,x_1{x}_2,x_1{x}_3,x_2{x}_1,x_2{x}_2,x_2{x}_3,x_3{x}_1,x_3{x}_2,x_3{x}_3)$，由于需要计算内积，所以在新的九维数据中，需要计算 $<f(x),f(y)>$的内积。再具体点，我们设置 $x=(1，2，3),y=(4，5，6)$，此时我们可以得到 $<f(x),f(y)>=1024$，这样一组数据看起来在高维空间内是还可以计算的，但是如果数据维度太大，这必然会导致计算量的倍增，占用很多资源
但从这组计算数据中可以看出，$K(x,y)=(<x,y>{)}^2,K(x,y)=1024$，两者结果相等，$K(x,y)=(<x,y>{)}^2=<f(x),f(y)>$，但是 $K(x,y)$ 计算起来却比 $<f(x),f(y)>$ 简单很多，也就是说只要用 $K(x,y)$ 来计算，效果和在高维空间中计算 $<f(x),f(y)>$ 是一样的效果，但计算的效率大大提升了，所以使用核函数的好处就是，可以在一个低维空间中去完成高维度（或者无限维度）的内机的计算。

所以，在支持向量机中，虽然是要将数据映射到一个高维空间当中，但我们最后只需要拿到数据的内积值，那么我们就可以先进行内积计算，再对在低维空间中得到的内积值映射到高维空间中去，得到的结果是一样的

Sklearn 求解支持向量机

在这里，对线性支持向量机和非线性支持向量机，都使用 Sklearn 做了简单的模型试验

支持向量机基本原理

对于低维线性不可分的问题，将其映射到高维空间来进行分类操作

例子：

# 生成随机数据 n_samples数据量 centers类别 random_state随机种子 cluster_std离散程度
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2,
                  random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

训练一个基本的SVM

from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear')
model.fit(X, y)

这里使用一个绘图模板进行可视化

#绘图函数
def plot_svc_decision_function(model, ax=None, plot_support=True):
    """Plot the decision function for a 2D SVC"""
    if ax is None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    
    # create grid to evaluate model
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    Y, X = np.meshgrid(y, x)
    xy = np.vstack([X.ravel(), Y.ravel()]).T
    P = model.decision_function(xy).reshape(X.shape)
    
    # plot decision boundary and margins
    ax.contour(X, Y, P, colors='k',
               levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--'])
    
    # plot support vectors
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0],
                   model.support_vectors_[:, 1],
                   s=300, linewidth=1, facecolors='none');
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model);

这条实线就是我们希望得到的决策边界，观察发现有3个点它们恰好都是边界上的点，它们就是我们的support vectors（支持向量）

在Scikit-Learn中, 它们存储在这个位置 support_vectors_（一个属性）

model.support_vectors_

array([[ 0.44359863,  3.11530945],
       [ 2.33812285,  3.43116792],
       [ 2.06156753,  1.96918596]])

观察可以发现，只需要支持向量就可以把模型构建出来，接下来再尝试一下，用不同数量的数据点，看看效果会不会发生变化

分别使用60个和120个数据点：

def plot_svm(N=10, ax=None):
    X, y = make_blobs(n_samples=200, centers=2,
                      random_state=0, cluster_std=0.60)
    X = X[:N]
    y = y[:N]
    model = SVC(kernel='linear', C=1E10)
    model.fit(X, y)
    
    ax = ax or plt.gca()
    ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    ax.set_xlim(-1, 4)
    ax.set_ylim(-1, 6)
    plot_svc_decision_function(model, ax)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, N in zip(ax, [60, 120]):
    plot_svm(N, axi)
    axi.set_title('N = {0}'.format(N))

通过这两个图可以看出，只要支持向量没有改变，其他的数据量不管怎么变化，得到的决策边界都不会发生改变

引入核函数的SVM

首先我们先用线性的核来看一下在下面这样比较难的数据集上还能分了吗？

from sklearn.datasets.samples_generator import make_circles
X, y = make_circles(100, factor=.1, noise=.1)

clf = SVC(kernel='linear').fit(X, y)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf, plot_support=False)

对于这种样本点，使用线性支持向量机已经不可分了，就需要使用高维核变换了

这里我们可以使用三维绘图将这个额外的数据维度可视化：

#加入了新的维度r
from mpl_toolkits import mplot3d
r = np.exp(-(X ** 2).sum(1))
def plot_3D(elev=30, azim=30, X=X, y=y):
    ax = plt.subplot(projection='3d')
    ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
    ax.view_init(elev=elev, azim=azim)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('r')

plot_3D(elev=45, azim=45, X=X, y=y)

# 加入径向基函数
clf = SVC(kernel='rbf', C=1E6)
clf.fit(X, y)

# 非线性支持向量机分类
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
            s=300, lw=1, facecolors='none')

使用这种核支持向量机，我们学习一个合适的非线性决策边界。这种核变换策略在机器学习中经常被使用

调节SVM参数: Soft Margin问题

调节 $C$ 参数

• 当C趋近于无穷大时：意味着分类严格不能有错误
• 当C趋近于很小的时：意味着可以有更大的错误容忍

试验 $C$ 参数对结果的影响

# 生成随机数据
X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');

这里设置了两个 $C$ 参数，分别为 $10.0$ 和 $0.1$

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=0.8)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for axi, C in zip(ax, [10.0, 0.1]):
    model = SVC(kernel='linear', C=C).fit(X, y)
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('C = {0:.1f}'.format(C), size=14)

通过结果看到， $C$ 参数越大，会对分类要求越严格，决策边界就会越小；$C$ 参数越小，会对分类要求越宽松，决策边界就会放大一些

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=1.1)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for axi, gamma in zip(ax, [10.0, 0.1]):
    model = SVC(kernel='rbf', gamma=gamma).fit(X, y)
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('gamma = {0:.1f}'.format(gamma), size=14)

调节 $gamma$ 参数

$gamma$ 参数控制着模型的复杂程度， $gamma$ 参数越大，模型会越复杂， $gamma$ 参数越小，模型会越精简

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=1.1)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for axi, gamma in zip(ax, [10.0, 0.1]):
    model = SVC(kernel='rbf', gamma=gamma).fit(X, y)
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('gamma = {0:.1f}'.format(gamma), size=14)

越复杂的边界，泛化能力越低，在这两个结果中，右边的简单的决策边界更为实用，他的泛化能力更强一些，更有实用价值