Matlab蒙特卡洛模拟二维伊辛模型相变过程

最新推荐文章于 2023-06-08 12:04:05 发布

置顶 icfg66

最新推荐文章于 2023-06-08 12:04:05 发布

阅读量1.8w

点赞数 40

分类专栏：统计物理文章标签：算法

本文链接：https://blog.csdn.net/qq_42556934/article/details/105370783

版权

统计物理专栏收录该内容

1 篇文章 1 订阅

订阅专栏

一、什么是伊辛模型

伊辛（Ising）模型是描述磁系统相变最简单的模型，但模型里自旋之间的相互作用赋予了它奇妙的特性，最有趣的就是对称性破缺。这一模型可以被推广用于研究连续的量子相变、基本粒子超弦理论、动力学临界行为等，甚至被认为可以描述深林火灾、交通拥堵、舆论传播等社会经济现象。
伊辛模型介绍
如图，每个格点的方向只有向上或向下两者状态，但临近的自旋之间有相互作用，而且点阵可以是一维、二维、三维、甚至更高维，这两个特点让伊辛模型的严格求解成为了世纪难题。为了定量描述这个系统的能量，我们假设第 $i$ 个格点的自旋为 $s_i$ ， $s_i$ 只能取+1或-1，如果相邻两个格点同方向，则它们相互作用的能量更小，设为 $- J$ ，如果为反方向，则为 $J$ ， $J$ 称为耦合系数，通常为正值，代表铁磁系统，如果 $J$ 为负值，则代表反铁磁系统。如果外磁场的强度为B，格点的自旋磁矩为 $\mu$ ，那么可以写出这个体系的哈密顿量：
$H=-J\sum_{<ij>}s_i s_j-\mu B \sum_{i=1}^N s_i$

自发对称性破缺

我们先定性地了解一下这个系统的性质，令外磁场零，当温度 $T\rightarrow 0$ 时，体系为了保持能量最低，所用的格点趋向于同方向，系统整体要么向下，要么向上，呈现强磁性。当温度 $T\rightarrow \infty$ 时，系统热运动占主导地位，格点方向呈现随机性，系统整体不带磁性，从上或从下观察体系，呈现出对称性，或者说无法通过系统磁性区分上或下。现在再考虑，当温度T从 $\infty$ 逐渐降温，那么系统必定存在某个温度 $T_c$ ，高于此温度时系统无磁性，低于此温度时，系统磁性逐渐加强。这个温度就是临界温度，也是相变点，系统从对称磁体转变为非对称磁体，而这就是对称性破缺，因为这种破缺不是外界扰动（如外加磁场）引起的，而是由内部的关联作用力造成的，所以称之为自发的对称性破缺。

上图就是对自发对称性破缺的定性描述，当逐渐降温到 $T_c$ 时，系统磁性开始出现分化，要么向下要么向上，最终平均的磁化强度 $\overline{s}$ 趋向于+1或-1。

我们感兴趣的问题主要有两个：第一，不同维度、不同分布的格点，其临界温度 $T_c$ 是多少；第二， $T_c$ 附近， $\overline{s}$ 随温度 $T$ 以什么样的幂指数 $\alpha$ 趋近于 $T_c$ ：
$\overline{s}\sim(T_c-T)^{\alpha}$

统计物理的思路

我们先考虑简单的9个格点的例子，实际格点数的量级为 $10^{29}$ 。
简单例子
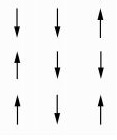
假设格点耦合强度 $J = 1$ ，那么这个9格点体系的能量为：
$E = [(- 1 + 1) + (- 2 + 1) + (2) + (2 - 1) + (- 3 + 1) + (- 1 + 2) + (- 1 + 1) + (- 1 + 2) + 2] / 2 = 2$
第一个格点有两个相邻格点，右边的与其同向，耦合能为-1，下面的与其反向，耦合能为1；第二个格点有三个相邻格点，左和下与其同向，耦合能为-2，右边与其反向，耦合能为1。类似的可以计算其余格点的耦合能。最后除以2是因为每个相互作用重复计算了一次。而这一特定分布以某概率P出现：
$P\varpropto e^{-E/kT}$
对于9个格点的体系，总共有 $2^9=512$ 种分布，每种分布的出现概率于其总能量有关，所以分布概率满足归一化条件。给定不同温度，我们可以计算出不同温度下平均磁化率的数学期望 $\overline{s}$ ，得到 $\overline{s}-T$ 的曲线。

但是对于粒子为 $10^{29}$ 量级的格点，可能的分布有 $2^{10^{29}}$ 种，根本不可能统计出结果。

一维的情况可以通过数学上的处理，最终可以提出N，并得到 $T_c=0$ ，也就是说一维的伊辛模型不会有自发的对称性破缺，这是因为一维的格点只有两个相邻格点，相互作用太弱，不足以对抗热运动，始终表现为整体0磁化率的对称状态。

二维的情况下，如果用平均场近似的方法（具体可以参考林宗涵的热力学与统计物理），基本思想是将相互作用的耦合能转化为外磁场强度，这就可以用近独立的模型来计算配分函数，进而得到所有的统计量，获得的临界温度为 $T_c= \frac{2J}{k}$ ，平均磁化率：
$\overline{s}\sim(T_c-T)^{1/2} ~~~~~~~~(T\rightarrow T_c^-)$

1944年，昂萨格推导出了二维伊辛模型的严格解，临界温度 $T_c=\frac {2.269J}{k}$ ，平均磁化率：
$\overline{s}\sim(T_c-T)^{1/8} ~~~~~~~~~(T\rightarrow T_c^-)$

二、二维伊辛模型的精确解

平均磁化率 $\overline s$

这里只列出二维伊辛模型精确解的结论，推导过于复杂，定义 $\beta\equiv \frac{1}{kT}$ ，则平均磁化率：
$\overline{s} =\begin{cases} 0,&{T>T_c} \\ [1-\sinh(2\beta J)^{-4}]^{1/8}, &{T\leq T_c}\end{cases}$
令 $\sinh(2\beta J)=0$ 可以解得： $T_c=\frac{2J}{k\ln(1+\sqrt{2})}\approx \frac{2.269J}{k}$ ，令 $T=T_c-\delta T$ ，小量泰勒展开化简可以得到：
$\overline{s}=[4·\frac{2J}{kT_c}\cosh(\frac{2J}{kT_c})·\frac{\delta T}{T_c}]^{1/8}=1.224[1-\frac{T}{T_c}]^{1/8}\sim(T_c-T)^{1/8}$
当 $T_c \rightarrow 0$ 时，容易得到结果为1，表面所有的格点同向，平均磁化率为1。

假设耦合强度 $J$ 等于1开尔文温度下的热运动能量，即 $J = k$ ，做出 $\overline{s}-T$ 曲线如下：
平均磁化强度s-T

平均能量和比热

另一个能够判断相变的参数是比热 $C_v=\frac{d \overline{E}}{dT}$ ，这里的 $\overline{E}$ 表示单个格点的平均能量，定性来看，当温度趋于0时，所有格点同向， $\overline{E}=-4/2=-2$ ，当温度趋于无穷时，格点方向随机，某格点四周平均有两个同向和两个方向， $\overline{E}=0$ 。其曲线如下(令 $J = k$ )：
能量与比热随温度的变化图

这里的比热在临界温度时会突然增大，表面临界温度附近变化有个小温度变化，需要吸收极大能量，这也很符合相变的特点。具体的计算公式和matlab代码详见附录A。

虽然大体了解了相变的过程，以及理论上的精确解，我们能否通过实验的方式，验证这一结论呢？借助计算机模拟这一过程来验证结果呢？

三、二维伊辛模型模拟

因为不可能遍历所有的格点组合，我们只能利用采样的方式去计算平均能量，采样的条件应该是体系在某个温度下已经平衡。计算机模拟的基本思想是，首先随机给定一种分布，在特定温度下，让体系趋向平衡，再在这个平衡体系中采样求平均。

假设体系有 $20\times 20$ 的格点，初始时同一分布，相当于温度很低；
我们设定一个希望“加热”到的平衡温度 $T_0$ ，接下来是模拟最关键的地方，如何改变格点的分布以趋向于设定温度 $T_0$ ？
1、我们先任意选择一个格点，计算改变这个格点的能量变化 $\Delta E$ ，因为体系出现的概率正比于 $e^{-E/kT}$ ，那么格点变化前后两个体系出现的概率比为 $e^{-\Delta E/kT}$ ，或者说格点改变的概率与不改变的概率比为： $1:e^{-\Delta E/kT}$ ，那么格点需要改变的概率为 $e^{-\Delta E/kT}$ ，因此我们产生一个(0,1)概率随机数，如果它小于 $e^{-\Delta E/kT}$ 则选择改变格点；
2、重复1的步骤，直到体系相对平稳，这个过程称为马尔可夫链，之后在平稳的体系下采样若干次并做统计平均，获得平均能量 $\overline E$ ，平均磁化率 $\overline s$ ，以及描述能量方差的比热 $C_v$ 。
3、设定另一个希望考察的温度，重复1、2步骤，获得该温度下的统计参数，并和理论值比较。

我们同样假设 $J = k$ ，选取格点数为 $20\times 20$ 。临界温度点附近，马尔可夫链长取5万次，采样数为25万次；其他温度点马尔可夫链长1万次，采样数为5万次。这是因为临界温度附近的涨落很大，需要更长的时间趋向平衡，需要更多的统计样本获得较准确平均值。详细的代码及解释可以参看附录B。

模拟平均磁化率 $\overline{s}-T$

平均磁化率的模拟结果

可以看出平均磁化率在临界温度附近很不稳定，这是因为临界相变时涨落很大的缘故，高温时的磁化率不是严格的零，可能与格点数少和马尔可夫链较短有关系，如何确定 $T_c$ 呢？通过平均磁化率求 $T_c$ 比较困难，一般是通过比热 $C_v$ 发散的位置确定 $T_c\approx 2.3$ ，参考下一部分。

选取T=1.7~2.2的16个数据点，拟合曲线：
$\ln\overline{s}\sim \alpha \ln(T_c-T)$
得到 $\alpha \approx 0.12,R^2=0.89$ ，这和理论值 $1 / 8 = 0.125$ 相当接近。

模拟平均能量 $\overline{E}-T$

平均能量和比热的模拟结果

在临界温度附近进行了较密集的温度取点，而且加长了马尔可夫链，但是仍能看到较大的涨落，可以通过这个现象来确定临界温度 $T_c\approx 2.3$ 。

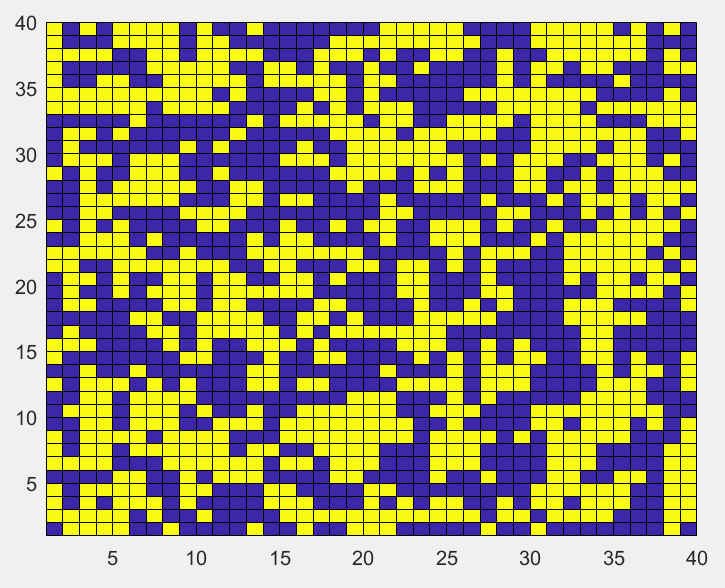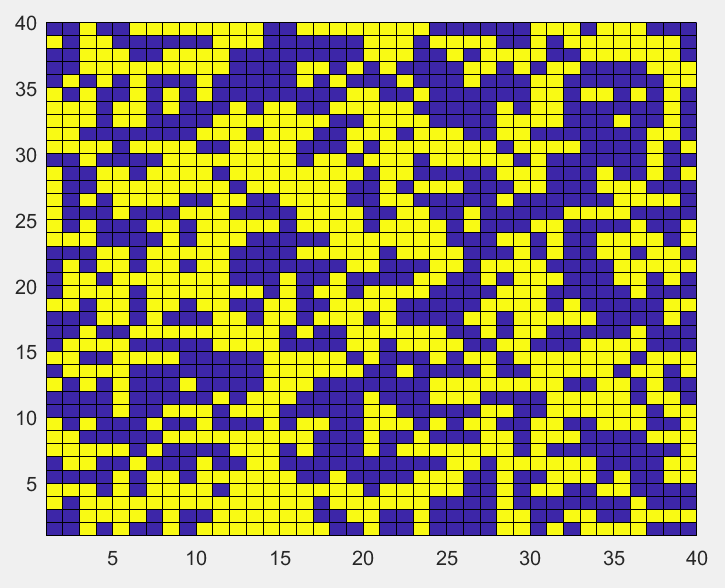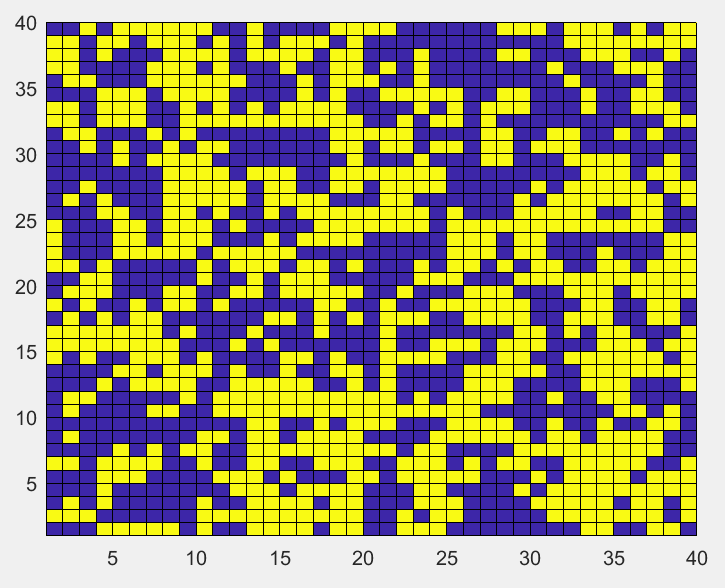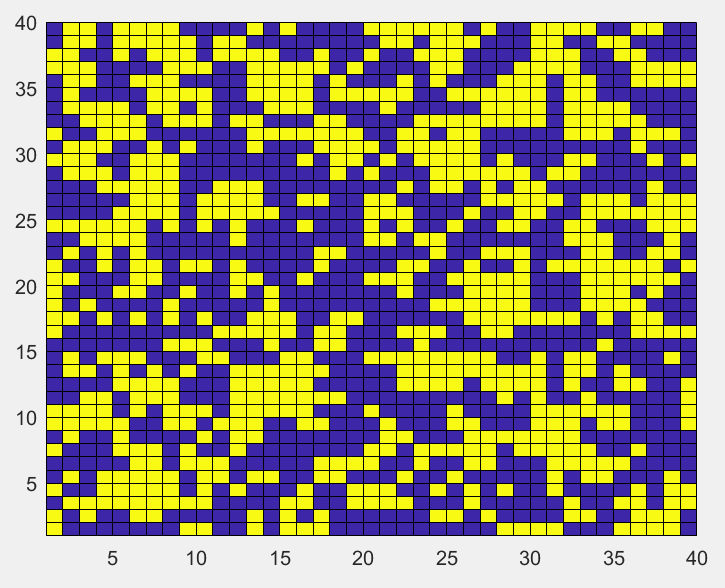
最后，让我们欣赏一下格点从同一分布到临界温度的变化过程吧，为了便于观察，选择40X40的格点，马尔可夫链长为1万：

初始同一分布的格点，逐渐趋向于高温 $T = 5$ 下的平衡态，格点最后呈现随机分布：
T=5，初始为有序

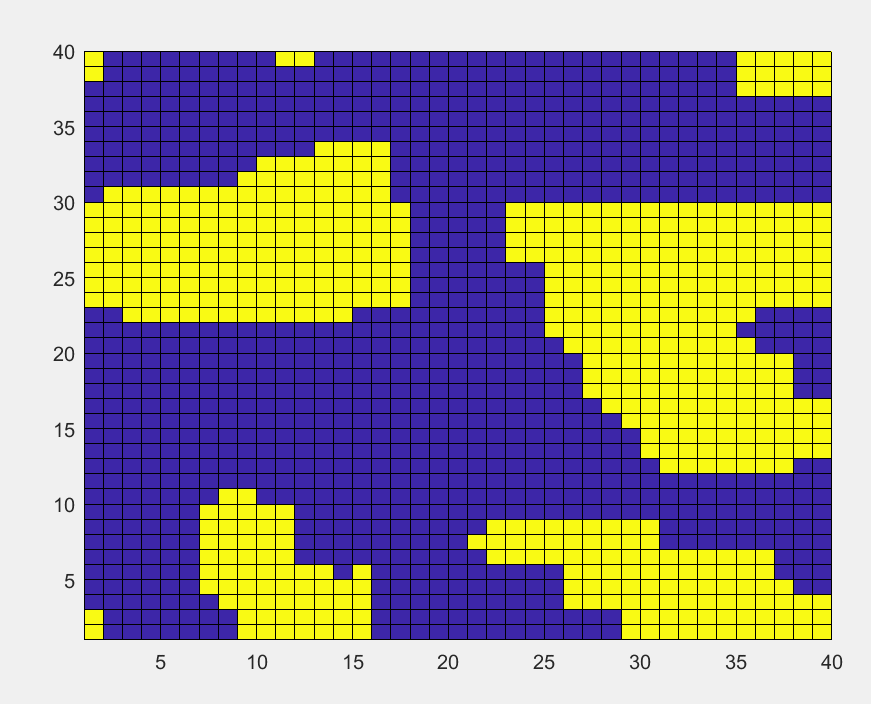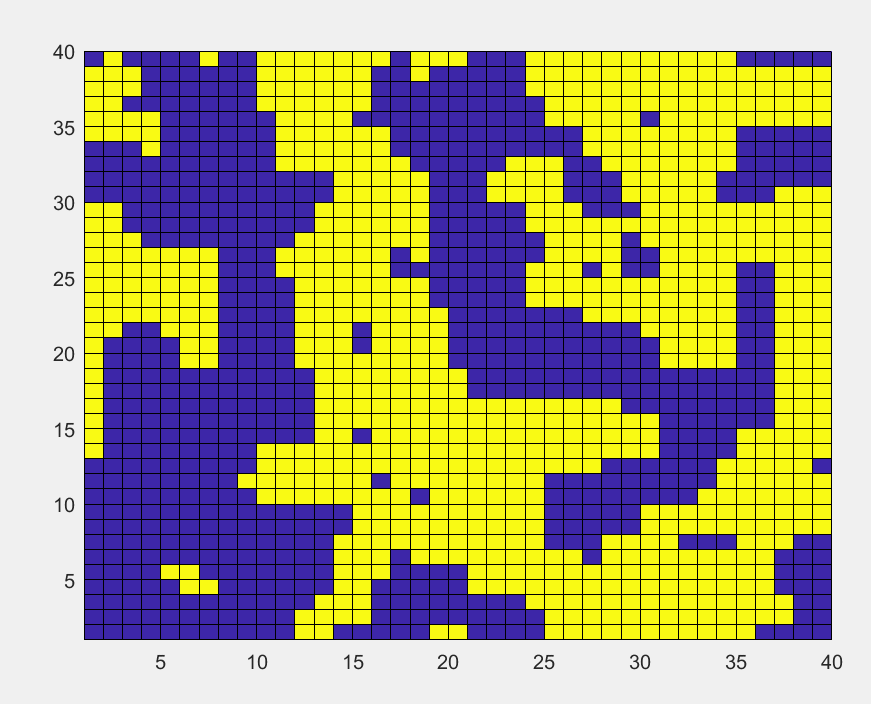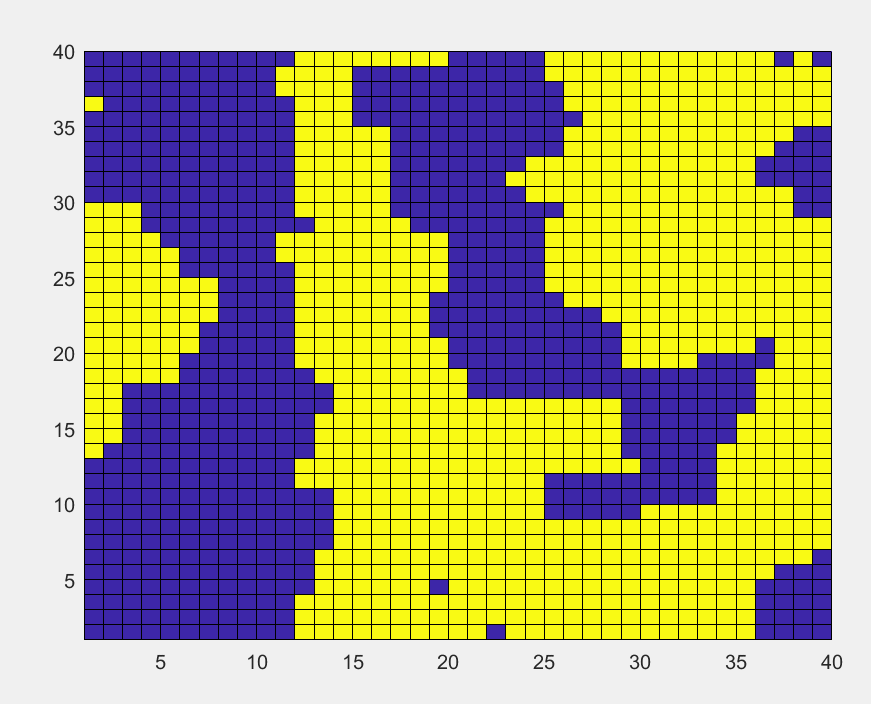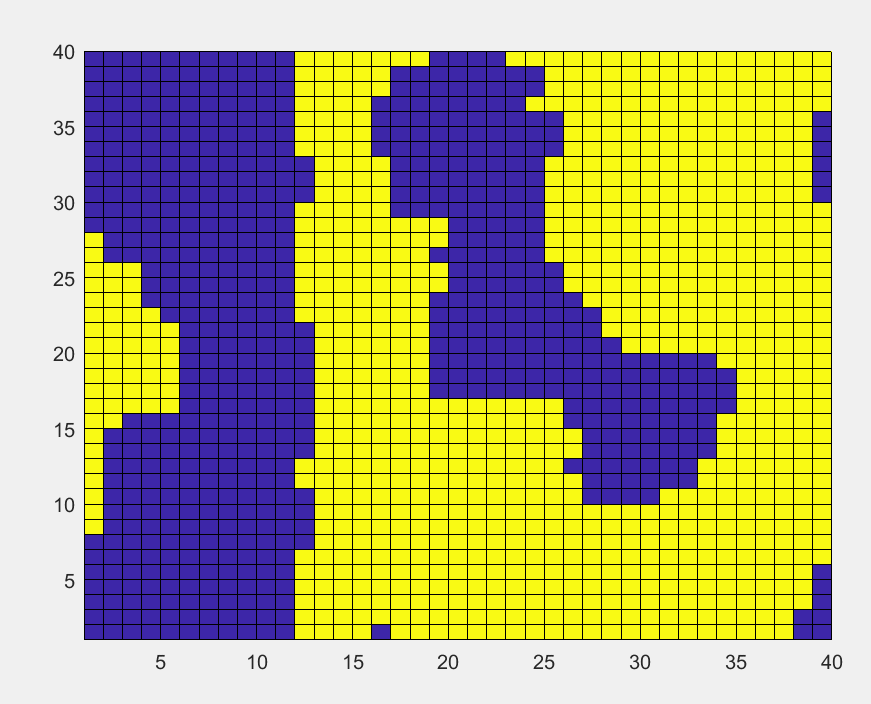
初始同一分布的格点，温度降低至 $T = 3$ 的平衡态，格点最后呈现小块状：
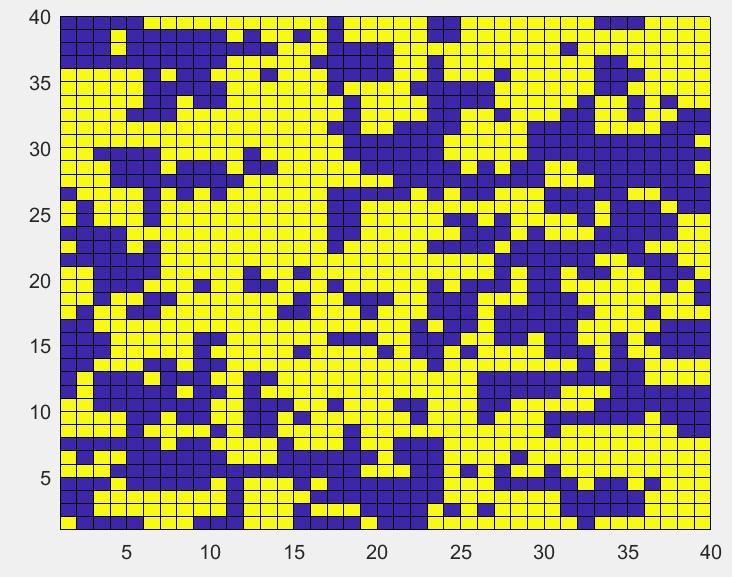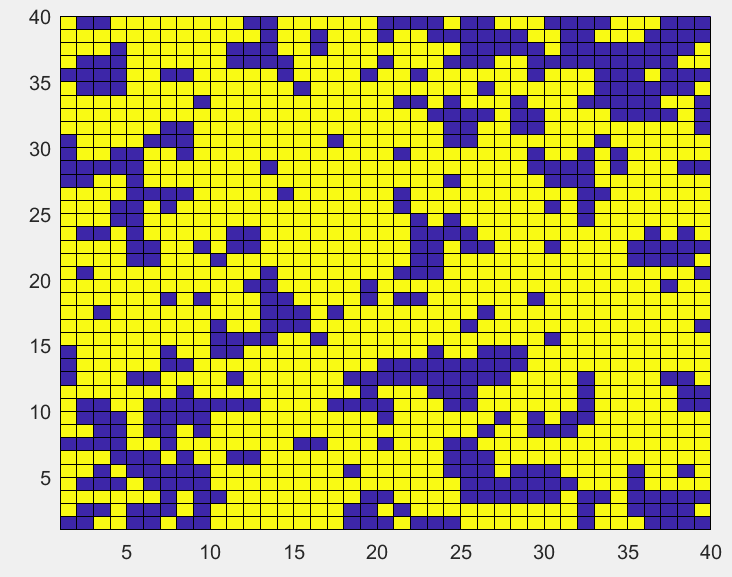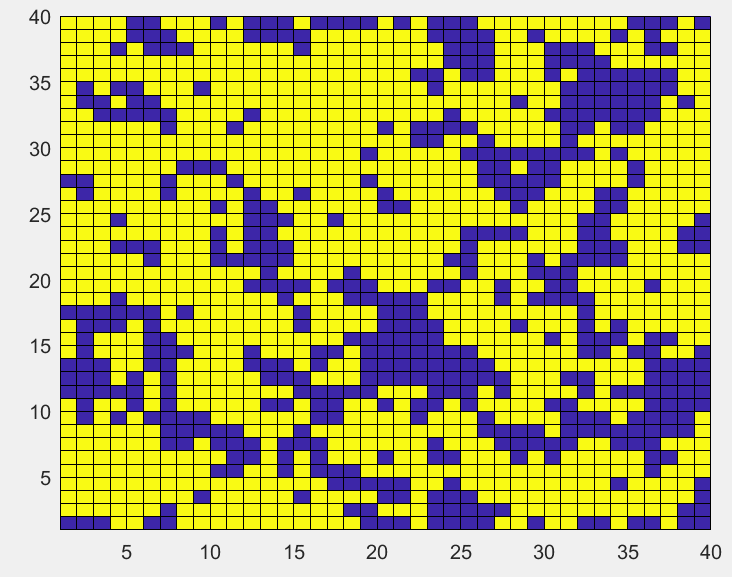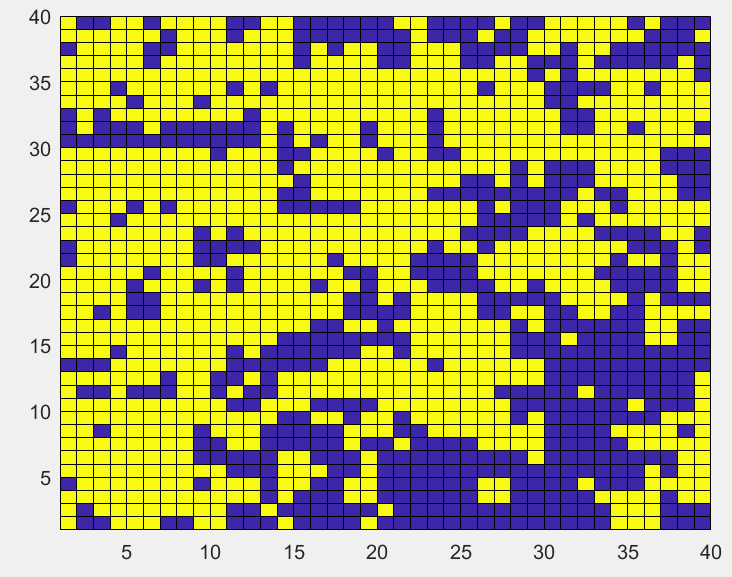
T=3，初始为有序

初始无序分布的格点，温度降低到临界温度 $T = 2.3$ 时，格点最后呈现的块状增大。
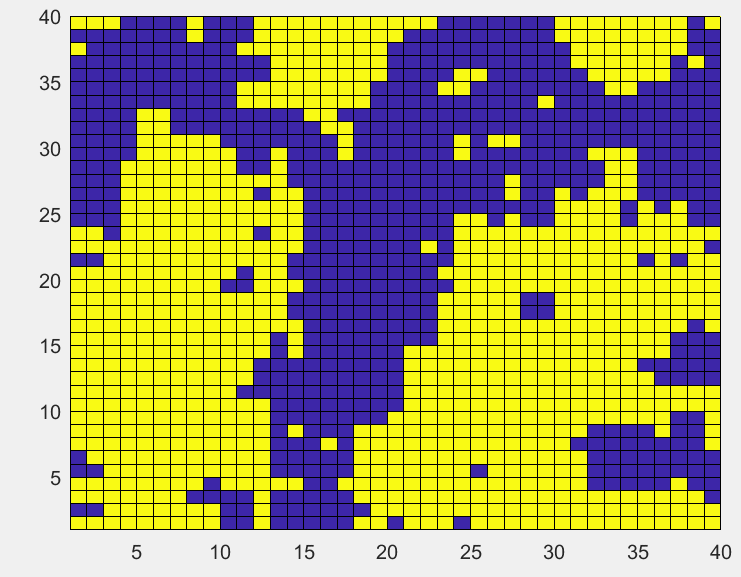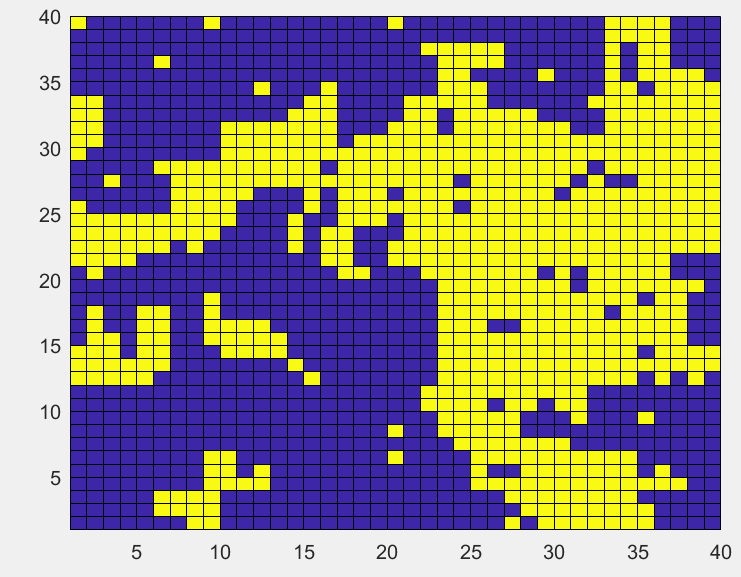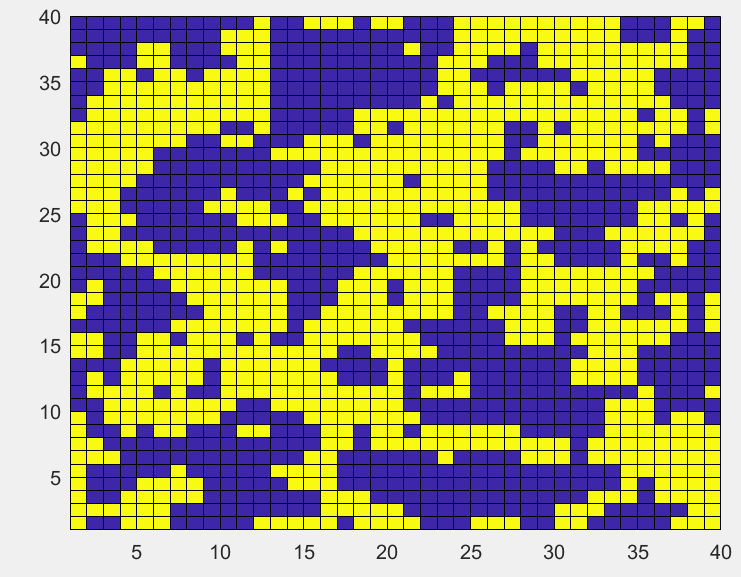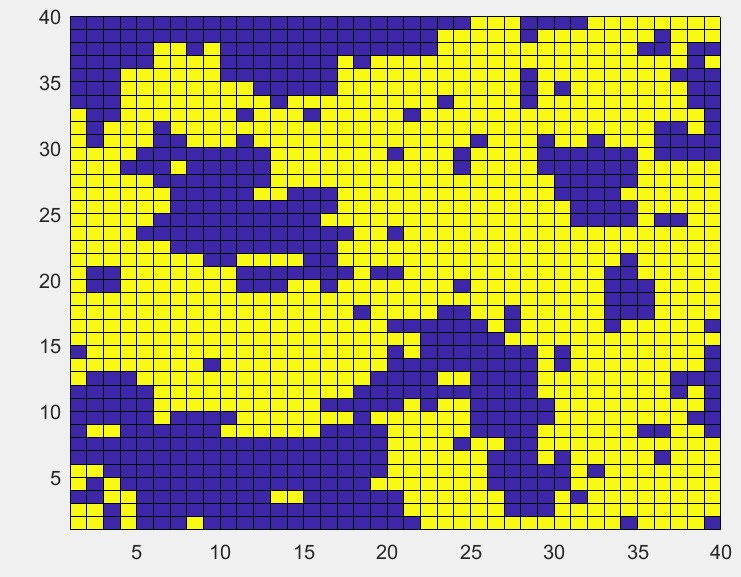
T=2.3，初始为无序

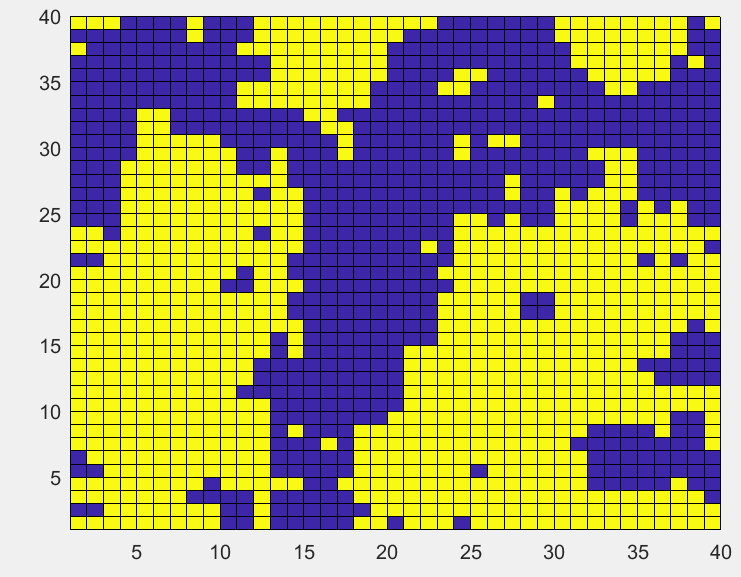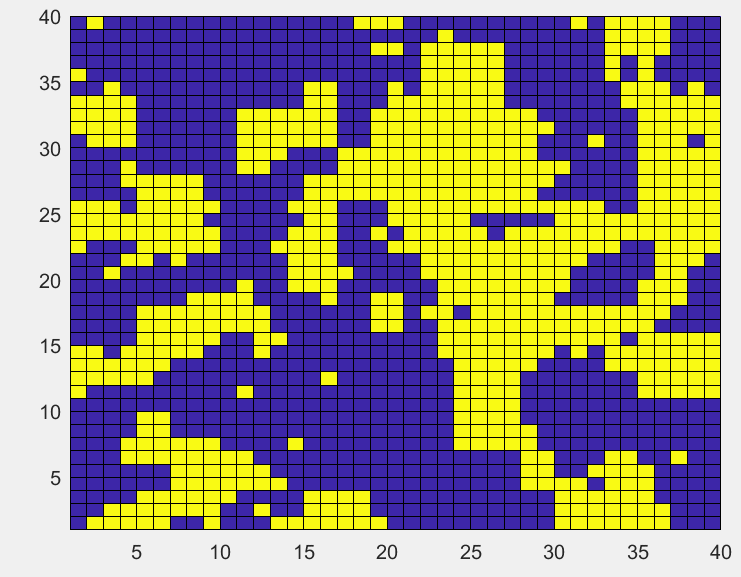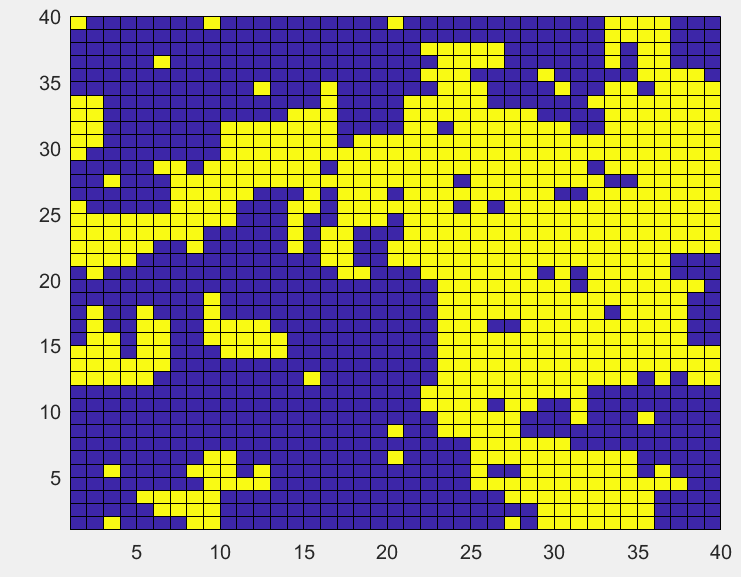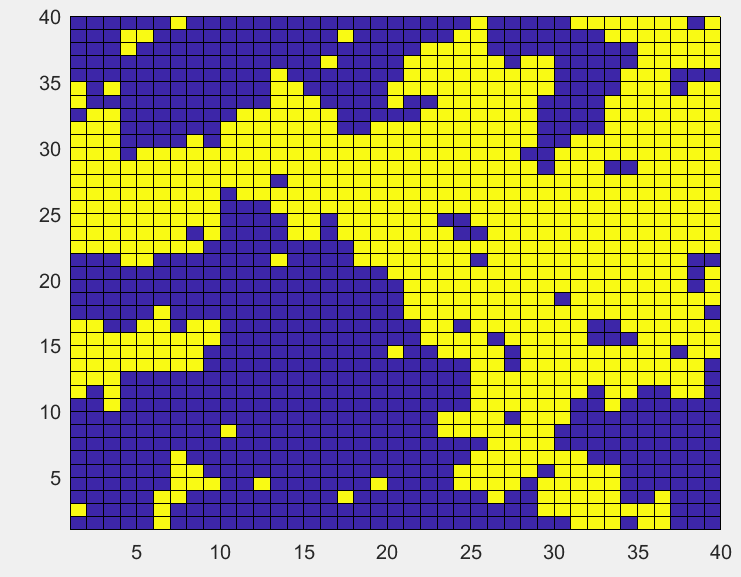
初始无序分布的格点，温度降低到临界温度以下 $T = 2$ ，格点最后呈现的大的块状，说明已经发生了明显的相变。
T=2，初始为无序

初始无序分布的格点，温度降低更多至 $T = 1$ ，格点越来越趋向于同一分布。
T=1，初始为无序

附录

A、平均能量和比热的精确解：(前方高能)

定义 $\beta \equiv 1/kT$
$\overline E=-J\cot(2\beta J)\times[1+\frac{2}{\pi}A·B(\lambda)]$
$\begin{cases} A\equiv 2\tanh(2\beta J)^2-1\\ B(\lambda)\equiv \int_0^{\pi/2} \frac{d\phi}{\sqrt{1-\lambda^2\sin\phi ^2}}\\ \lambda\equiv \frac{2\sinh(2\beta J)}{\cosh(2\beta J)^2} \end{cases}$
帝国主义都是纸老虎，我们仔细发现，只要确定了温度 $T$ 或 $\beta$ ，那么可以依次确定 $\lambda,B(\lambda),A,\overline E$ ，也就是平均能量和温度是一一对应的，最后通过求导得到比热 $C_v=d \overline E/d T$ 。

%matlab code
clear;clc;
beta=0.1:0.01:1; %温度从10到1
for i=1:1:size(beta,2);%遍历beta
lambda=2.*sinh(2.*beta(i))./cosh(2.*beta(i)).^2;%计算lambda
phi=linspace(0,pi/2,1000);%求B的积分参数
b=1./sqrt(1-lambda.^2.*sin(phi).^2);
B=trapz(phi,b);%积分B(lambda)
A=2*tanh(2.*beta(i)).^2-1;
e_bar(i)=-coth(2.*beta(i)).*(1+2/pi.*A.*B); %每个格点的平均能量
end
%%
plot(1./beta,e_bar,'k','LineWidth',2);hold on;%E-T曲线
beta1=beta(2:end)/2+beta(1:end-1)/2;
cv=-beta1.^2.*diff(e_bar)./diff(beta); %对能量求导得到比热
plot(1./beta1,cv,'r','LineWidth',2);

平均能量和比热随温度的变化图

B、蒙特卡洛马尔可夫链模拟二维伊辛模型相变过程

具体细节详见代码：

%matlab code
clear;clc;
n=10000;                       %马尔可夫链长度1万
ns=20;                          %20*20的格点 
beta_mc=(0.1:0.01:0.4);         %温度从10到2.5,链长1万，样品长5万
%T_mc=(2.1:0.01:2.4);          %第三批模拟温度设定，临界温度附近取点更密集，还要调整n=50000
%beta_mc=1./T_mc;
tic;                               %计时用，n=10000时，通常需要跑一分多钟
for jj=1:1:size(beta_mc,2)
X=sign(rand(ns,ns));        %所有格点方向一致，相当于从0度开始升温
%马尔可夫链长度为5万次
for j=1:1:n
    %随机选取一个格点，行列存储在index[1,2]
    index=unidrnd(ns,1,2);      
    % 利用周期性边界条件，分别计算格点上下左右四个点行列坐标
    tmp1=rem(index(1),ns)+1;tmp2=rem(index(1)+1,ns)+1;tmp3=rem(index(1)-1,ns)+1;
    tmp4=rem(index(2),ns)+1;tmp5=rem(index(2)+1,ns)+1;tmp6=rem(index(2)-1,ns)+1;
    % 计算改变格点方向后的能量变化
    cen=X(tmp1,tmp4);right=X(tmp1,tmp5);left=X(tmp1,tmp6);
    up= X(tmp2,tmp4);down= X(tmp3,tmp4);
    deE=2*cen*(right+left+up+down);
    % 判断是否改变格点
    if rand<exp(-deE*beta_mc(jj))
        X(tmp1,tmp4)=-X(tmp1,tmp4);
    end
end    

% 取样5万次，平衡时同样需要判断是否改变格点
for j=1:1:5*n
    index=unidrnd(ns,1,2);
    % 利用周期性边界条件，分别计算格点上下左右四个点行列坐标
    tmp1=rem(index(1),ns)+1;tmp2=rem(index(1)+1,ns)+1;tmp3=rem(index(1)-1,ns)+1;
    tmp4=rem(index(2),ns)+1;tmp5=rem(index(2)+1,ns)+1;tmp6=rem(index(2)-1,ns)+1;
    % 计算改变格点方向后的能量变化
    cen=X(tmp1,tmp4);right=X(tmp1,tmp5);left=X(tmp1,tmp6);
    up= X(tmp2,tmp4);down= X(tmp3,tmp4);
    deE=2*cen*(right+left+up+down);
    % 判断是否改变格点
    if rand<exp(-deE*beta_mc(jj))
        X(tmp1,tmp4)=-X(tmp1,tmp4);
    end
    %计算一种特定分布时的平均磁化率
    m(j)=abs(mean(mean(X)));  
	%计算一种特定分布时的平均能量
    Xt1=X;Xt1(1,:)=[];Xt1=[Xt1; X(1,:)];
    Xt2=X;Xt2(:,1)=[];Xt2=[Xt2, X(:,1)];
    e(j)=-mean(mean(X.*Xt1+X.*Xt2));
end
% 特定温度下的统计量
m_bar(jj)=mean(m);   
e_bar(jj)=mean(e);
cv_bar(jj)=beta_mc(jj)^2*ns^2*std(e)^2;
end
toc;
% 作图观察
figure(1);
plot(1./beta_mc,m_bar,'ko');
figure(2);
plot(1./beta_mc,e_bar,'ko');
figure(3);
plot(1./beta_mc,cv_bar,'ro');

20X20格点，从同一分布开始升温，分布进行了三批温度选择：

$\beta=(0.1:0.01:0.4)$ 31个温度点， $T\in[2.5,10]$ 马尔可夫链长度为1万次，采样5万次。
$T = (0.1 : 0.1 : 2.1)$ 21个温度点，$马尔可夫链长度为1万次，采样5万次。
$T = (2.1 : 0.01 : 2.4)$ 31个温度点，马尔可夫链长度为5万次，采样25万次。

原文

icfg66

关注

40
点赞
踩
142

收藏

觉得还不错? 一键收藏
26
评论
Matlab蒙特卡洛模拟二维伊辛模型相变过程

一、什么是伊辛模型伊辛（Ising）模型是描述磁系统相变最简单的模型，但模型里自旋之间的相互作用赋予了它奇妙的特性，最有趣的就是对称性破缺。这一模型可以被推广用于研究连续的量子相变、基本粒子超弦理论、动力学临界行为等，甚至被认为可以描述深林火灾、交通拥堵、舆论传播等社会经济现象。如图，每个格点的方向只有向上或向下两者状态，但临近的自旋之间有相互作用，而且点阵可以是一维、二维、三维、甚至更高维...
复制链接

扫一扫