求旋转体侧面积

首先判断曲线是否关于x轴，y轴或原点对称，如果对称，则只取一半。

一条曲线可以做多次取一半的操作，比如星形线，关于x轴对称，则可以去掉x轴下方的部分，剩下的部分依然关于y轴对称，因此可以再去掉y轴右侧的部分，两次操作后只保留了第一象限的部分

接着，看所给函数类型

以下以绕x轴旋转为例

1.直角坐标系，y=y(x),x取值范围为[a,b]，则求

实际上，这个方程是求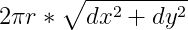积分后得到的值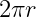，是圆的周长，因为绕x轴，所以在积分式子中r取|y|，如果是绕y轴旋转，那么r代入|x|。

而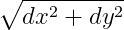则是侧面长度。把侧面的长度近似看成一截很短的圆柱的高，两者相乘便近似为很短一段长度上的圆柱体表面积。

积分后，便为整个旋转体表面积

2.参数方程，t取值为[α,β]，则求

之后，根据求出来的旋转体侧面积，推出原来的旋转体侧面积，因为经过取一半操作后，上面式子求出来的面积并不是完整的旋转体侧面积

例：求星形线绕x轴旋转形成的旋转体侧面积

根据分析，只保留第一象限的曲线，对这个曲线旋转得到的旋转体求面积，为

根据图像分析，整体的侧面积应为该部分的两倍，所以答案为(12πa^2)/5