求旋转体体积

1.圆盘法

将图形想象成无数个超级小的圆柱体叠在一起，则dV=πr^2dx或dy，其中r根据函数和旋转轴确定，dx或dy由旋转轴的选择确定。一般情况下（即y用x表示），绕x轴或y=a旋转时，用圆盘法

例如y=x^2与y=2和y轴围成的图形绕y轴旋转，则r=√(y)，选择dy，积分上下限为0到2

y=x^2与x=2和x轴围成的图形绕x轴旋转，则r=x^2，选择dx，积分上下限为0到2

假如旋转体中，每一层都是两个同心圆围成的区域，即整个旋转体类似于一个甜甜圈，则

其中f(x)离旋转轴y=a更远

例如，下图是y=-x+4和y=x的图像，两者与y轴围成的图像绕x轴旋转时，f(x)为-x+4，a=0，但假如绕y=4旋转，此时f(x)为x，a=4

2.柱壳法

将图形看作是一堆圆柱体计算厚度的表面一层套在一起（更通俗一点，就是长短和半径不同的厕纸纸筒套在一起），此时dV=2πr*|f(x)|dx，r由旋转轴和函数确定，选择|f(x)|dx还是|f(y)|dy由旋转轴确定， 一般情况下（即y用x表示），绕y轴或x=a旋转时，用圆盘法

因为一个柱壳的体积就是周长乘以高度乘以厚度，周长为2πr，高度为|f(x)|，厚度为dx。

例如，求y=x^2-2x，x=1，x=3，x轴围成的图形绕y轴旋转得到的体积。此时x=r

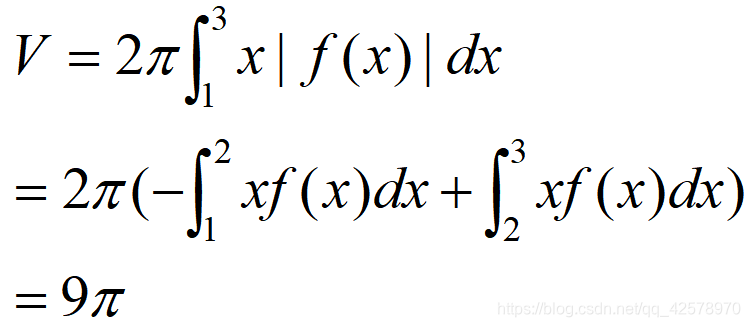
在这种情况下，只需要分别求f大于0和小于0的部分的体积，相加即可，不会出现上面那种一部分减去另一部分的情况