问题 设D为一平面区域,L为不穿过D内部的共面直线,求D绕L旋转一周所成旋转体的体积。
结论 由连续曲线y=f(x),其中f(x)≥0,以及直线x=a,x=b及x轴所围成的曲边梯形D绕不穿过曲边梯形内部的共面直线L:Ax+By+C=0旋转一周所成的旋转体的体积为:
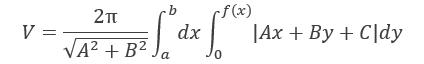
证明 曲边梯形D上任取一点P(x,y),则x,y的变化范围为0≤y≤f(x);a≤x≤b.点P(x,y)到L的距离

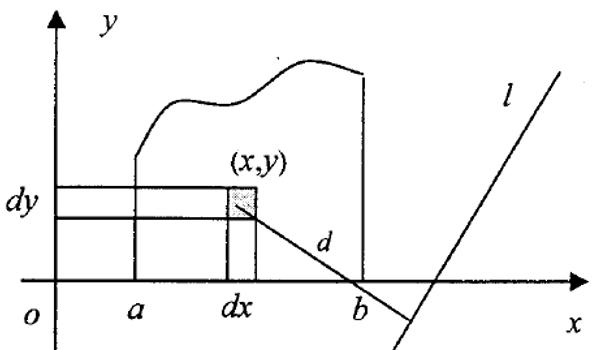
在点P(x,y)处分别给出x,y的微分dx,dy,得曲边梯形上的面积微元dσ,且知dσ=dxdy。面积为dσ的面积微元绕L旋转所形成的立体体积微元
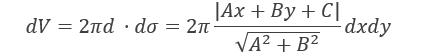
所以有
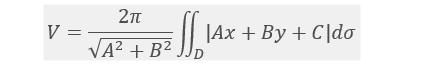
几种特殊情形
(1) D: g(x)

(2) D: u(y)
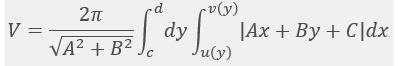
(3) D: r1(q)2(q), a
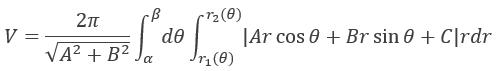
(4) D: 0
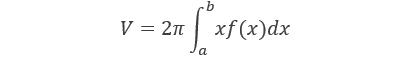
(5) D: 0
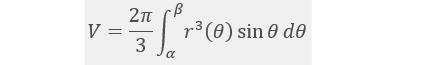
(6) D: 0
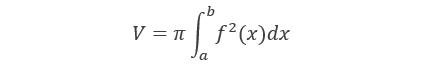
例子
1. 求椭圆x2+2y2=1绕直线x+y=2旋转一周所成旋转体的体积。
解 平面区域D可表示为:
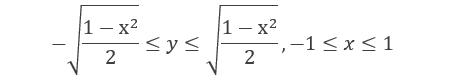
区域D与直线x+y=2的位置关系如下图:
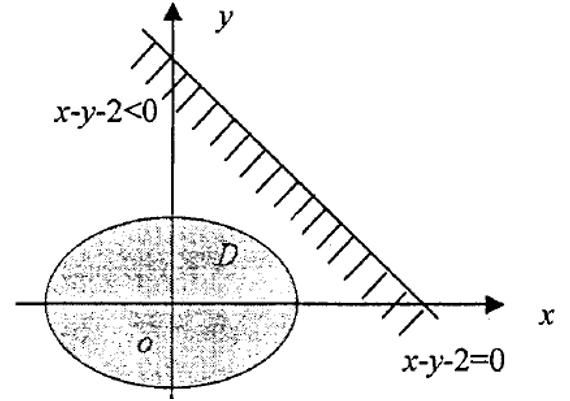
对区域D内任意点都有:x + y –2<0,所以
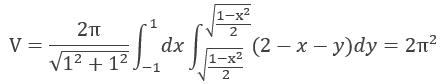
2. 求心形线r=4(1+cosθ)及射线θ=0及θ=π/2所围成的图形绕极轴旋转一周所成旋转体的体积.
解 区域D为:
0
对D内任意点都有y>0,所以有
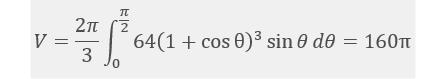







 博客探讨了如何计算平面区域绕固定直线旋转一周形成的旋转体体积。通过曲边梯形D的边界条件和距离公式,利用积分原理推导出体积公式,并给出了两种特殊情形的求解方法。具体应用中,例如椭圆绕直线旋转和心形线绕极轴旋转的体积计算被详细阐述。
博客探讨了如何计算平面区域绕固定直线旋转一周形成的旋转体体积。通过曲边梯形D的边界条件和距离公式,利用积分原理推导出体积公式,并给出了两种特殊情形的求解方法。具体应用中,例如椭圆绕直线旋转和心形线绕极轴旋转的体积计算被详细阐述。
















 928
928

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








