旋转体体积的两种常用求法及单位转换问题

例

如图所示，求由$y=x^2$绕y轴旋转而成的旋转体的体积

方法一：对y积分（Disks）

如图所示，盘片的面积为$\pi x^2$，厚度为$dy$的盘片的体积为$dV=\pi x^{2}dy$ ，则体积$V$的计算方法如下：
$$V={\int }_0^a\pi x^{2}dy$$
$$\text{换元}y=x^2$$
$$V={\int }_0^a\pi ydy={\pi \frac{y^2}{2}|}_0^a=\pi \frac{a^2}{2}$$

方法二：对x积分（Shells）

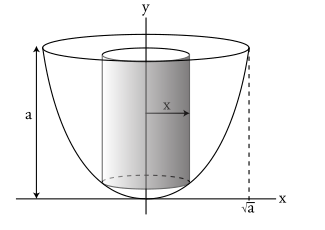
$x$为圆柱的半径，圆柱的厚度为$dx$，高为$a-x^2$，则
$$dV=\left(a-x^2\right)\left(2\pi x\right)dx$$
$$V={\int }_0^{\sqrt{a}}\left(a-x^2\right)\left(2\pi x\right)dx=2\pi {\int }_0^{\sqrt{a}}\left(ax-x^3\right)dx={2\pi \left(\frac{a{x}^2}{2}-\frac{x^4}{4}\right)|}_0^{\sqrt{a}}=\frac{\pi a^2}{2}$$

代值

如果$a=1m$，代入$V=\frac{\pi a^2}{2}$，得$V=\frac{\pi }{2}{m}^3$
如果$a=100cm$，代入$V=\frac{\pi a^2}{2}$，得$V=5000\pi c{m}^3$
虽然$1m=100cm$，但是$\frac{\pi }{2}{m}^3\ne 5000\pi c{m}^3$ ，为什么会出现这种现象呢？到底哪个是正确的呢？
其实两个都是正确的，只不过两个旋转体的体积确实不同，虽然他们高度相同，但它们的宽度不同。
对于$a=1m$，当$y=1m$时$x=\pm 1m$，切面如图所示

对于$a=100cm$，当$y=100cm$时$x=\pm 10cm$，切面如图所示

可以看到它们虽然高度相同，但宽度是不同的，所以计算出来的体积也不同。