目录
- 问题2.15
- (1)画散点图
- (2) x {x} x与 y y y之间是否大致呈线性关系
- (3)用最小二乘估计求回归方程
- (4)求回归标准误差 σ ^ \hat\sigma σ^
- (5)给出 β ^ 0 \hat\beta_0 β^0与 β ^ 1 \hat\beta_1 β^1的置信度为95%的区间估计
- (6) x x x与 y y y的决定系数
- (7)对回归方程做方差分析
- (8)做回归系数 β 1 \beta_1 β1的显著性检验
- (9)做相关系数的显著性检验
- (10)对回归方程作残差图并做相应的分析
- (11)该公司预计下一周签发新保单 x 0 = 1000 x_0=1000 x0=1000张,需要的加班时间时多少?
- (12)给出 y 0 y_0 y0的置信度为95%的精确预测区间和近似预测区间
- (13)给出 E ( y 0 ) E(y_0) E(y0)的置信度为95%的区间估计
- 例题2.1(火灾)
- 数据与源代码链接
先做声明,代码中表示的只是按照理论计算的过程,并非R语言的内置函数,大家可以用R语言内置的回归函数做对比,帮助理解学习。本书引用书籍为何晓群的《应用回归分析》
问题2.15
问题如下:


完整代码如下
setwd("E:/AllClass/junior1/RegressionAnalysis/unit2")#设置文件路径
#保留原路径setwd("C:/User/10854/documents")
#以下利用理论方法使用一元回归模型
#导入数据
data<-read.csv("2-7.csv")#书本2.15,表数据2-7
x<-data[,1]
y<-data[,2]
n<-length(x)
split.screen(c(1,3))
screen(1)
plot(x,y,pch=16)
title(main="数据散点图")
#求均值与回归变量lxx,lyy,lxy
meanx<-mean(x)
meany<-mean(y)
lxx<-sum((x-meanx)^2)
lyy<-sum((y-meany)^2)
lxy<-sum((x-meanx)*(y-meany))
#回归系数估计
beta_1<-lxy/lxx#beta_1
beta_0<-meany-beta_1*meanx#beta_0
screen(2)
plot(x,y,pch=16)
points(x,beta_0+beta_1*x,type="l")
title(main="回归图")
#预测值与平方和
y_hat<-beta_0+beta_1*x
sse<-sum((y_hat-y)^2)#残差平方和
ssr<-sum((y_hat-meany)^2)#回归平方和
sst<-ssr+sse#总离差平方和
#回归误差ε的方差sigma估计
sigma_hat<-sqrt(1/(n-2)*sse)
#对bet_0、beta_1的95%区间估计
alpha<-0.05
#beta_0,beta_1的分布标准差
sd.beta_0<-sqrt((1/n+(meanx^2)/lxx))*sigma_hat
sd.beta_1<-sqrt(sigma_hat^2/lxx)
beta_1l<-beta_1-qt(1-alpha/2,n-2)*sd.beta_1#beta_1置信下限
beta_1u<-beta_1+qt(1-alpha/2,n-2)*sd.beta_1#beta_1置信上限
beta_0l<-beta_0-qt(1-alpha/2,n-2)*sd.beta_0#beta_0置信下限
beta_0u<-beta_0+qt(1-alpha/2,n-2)*sd.beta_0#beta_0置信上限
#remark
#qt是求出置信度1-α对应的统计量值t(1-α)
#dt是求出统计量对应的置信度值,即p值(这里用不上t分布)
#dt返回概率密度,pt返回分布函数,qt返回分位数函数,rt生成随机数。
#qf\df都是同理,对应的是F分布
#计算xy决定系数
R<-ssr/sst
#回归方程的显著性检验
#法一方差分析F检验
f<-(ssr/1)/(sse/(n-2))
p1<-pf(f,1,n-2)#F为统计量、1为第一个自由度,n-2为第二个自由度
#法二回归系数的beta_1的t检验
t1<-beta_1/sd.beta_1#t统计量
p2<-pt(t1,n-2)
#法三相关系数r的t检验
r<-lxy/(sqrt(lxx*lyy))
t2<-sqrt(n-2)*r/sqrt(1-r^2);
p3<-pt(t2,n-2) #p值
#残差图
screen(3)
e<-y_hat-y #残差
n<-length(e)
sigma_u<-seq(2*sigma_hat,2*sigma_hat,length.out=n) #残差2σ原则
sigma_l<-seq(-2*sigma_hat,-2*sigma_hat,length.out=n)
plot(x,e,pch=16,ylim=c(5,-5))
points(x,sigma_u,type="l") #画2σ上下界
points(x,sigma_l,type="l")
title(main="残差图")
#预测广告费用为1000万元时,销售达多少
x0<-1000
y0<-beta_0+beta_1*x0
#因变量新值得95%置信区间
h00<-1/n+((x0-meanx)^2)/lxx
y0_l<-y0-qt(1-alpha/2,n-2)*sqrt(1+h00)*sigma_hat#预测新值得置信下限
y0_u<-y0+qt(1-alpha/2,n-2)*sqrt(1+h00)*sigma_hat#预测新值得置信上限
#近似置信区间
y0_l_ <- y0-2*sigma_hat
y0_u_ <- y0+2*sigma_hat
#因变量新值得平均值的95%置信区间
y0_l_E<-y0-qt(1-alpha/2,n-2)*sqrt(h00)*sigma_hat#预测新值均值得置信下限
y0_u_E<-y0+qt(1-alpha/2,n-2)*sqrt(h00)*sigma_hat#预测新值均值得置信上限
#以下利用R函数回归
(1)画散点图
1.1问题求解
1.1.1输入
#导入数据
data<-read.csv("2-7.csv")#书本2.15,表数据2-7
x<-data[,1]
y<-data[,2]
n<-length(x)
# split.screen(c(1,3))
# screen(1)
plot(x,y,pch = 16)
title(main="数据散点图")
1.1.2输出
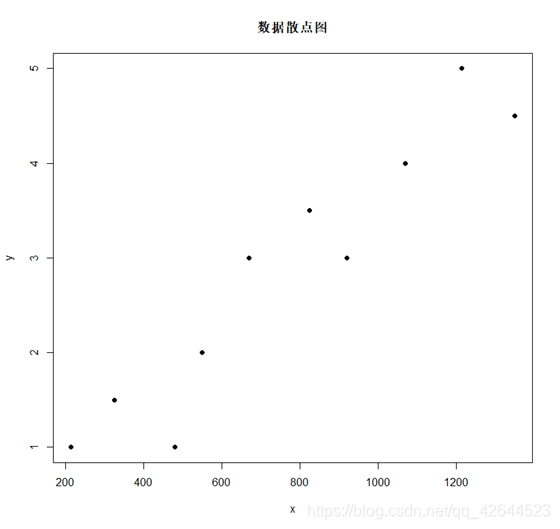
(2) x {x} x与 y y y之间是否大致呈线性关系
由第一问的散点图,大致正相关,并且呈线性关系
(3)用最小二乘估计求回归方程
3.1问题分析
先求样本均值
x
ˉ
=
Σ
x
i
,
y
ˉ
=
Σ
y
i
\bar{x}=\Sigma{x_i},\bar{y}=\Sigma{y_i}
xˉ=Σxi,yˉ=Σyi
L x x = Σ i = 1 n ( x i − x ˉ ) 2 L_{xx}=\Sigma_{i=1}^{n}(x_i-\bar{x})^2 Lxx=Σi=1n(xi−xˉ)2
L y y = Σ i = 1 n ( y i − y ˉ ) 2 L_{yy}=\Sigma_{i=1}^{n}(y_i-\bar{y})^2 Lyy=Σi=1n(yi−yˉ)2
L x y = Σ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) L_{xy}=\Sigma_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) Lxy=Σi=1n(xi−xˉ)(yi−yˉ)
则回归系数的估计如下:
β
^
1
=
L
x
x
L
y
y
\hat\beta_1=\frac{L_{xx}}{L_{yy}}
β^1=LyyLxx
β ^ 0 = y ˉ − β 1 x ˉ \hat\beta_0=\bar{y}-\beta_1\bar{x} β^0=yˉ−β1xˉ
得到回归方程如下:
y
i
=
β
^
0
+
β
^
1
x
i
y_i=\hat\beta_0+\hat\beta_1x_i
yi=β^0+β^1xi
3.2问题求解
3.2.1输入
#求均值与回归变量lxx,lyy,lxy
meanx<-mean(x)
meany<-mean(y)
lxx<-sum((x-meanx)^2)
lyy<-sum((y-meany)^2)
lxy<-sum((x-meanx)*(y-meany))
#回归系数估计
beta_1<-lxy/lxx#beta_1
beta_0<-meany-beta_1*meanx#beta_0
# screen(2)
plot(x,y,pch=16) #散点
points(x,beta_0+beta_1*x,type="l") #回归线
title(main="回归图")
3.2.2输出
得出各参数
| 统计量 | 统计值 |
|---|---|
| x ˉ \bar{x} xˉ | 762 |
| y ˉ \bar{y} yˉ | 2.85 |
| L X X L_{XX} LXX | 1297860 |
| L x y L_{xy} Lxy | 4653 4653 4653 |
| L y y L_{yy} Lyy | 18.525 |
| β ^ 0 \hat\beta_0 β^0 | 0.118 |
| β ^ 1 \hat\beta_1 β^1 | 0.00359 |
| 回归方程: | |
| $$ | |
| y_i=0.118+0.00359x_i | |
| $$ |
回归图:

(4)求回归标准误差 σ ^ \hat\sigma σ^
4.1问题分析
分别得出
S
S
E
=
Σ
(
y
i
−
y
^
)
2
SSE=\Sigma(y_i-\hat{y})^2
SSE=Σ(yi−y^)2
标准误差
σ
{\sigma}
σ的无偏估计为:
σ
^
=
1
n
−
2
Σ
i
=
1
n
e
i
2
=
1
n
−
2
Σ
(
y
i
−
y
^
)
2
\hat\sigma={\frac{1}{n-2}}\Sigma_{i=1}^{n}e_{i}^2={\frac{1}{n-2}}\Sigma\left(y_i-\hat{y}\right)^2
σ^=n−21Σi=1nei2=n−21Σ(yi−y^)2
4.2问题求解
4.2.1输入
sse<-sum((y_hat-y)^2)#残差平方和
#回归误差ε的方差sigma估计
sigma_hat<-sqrt(1/(n-2)*sse)
4.2.2输出
S S E = 1.843 , σ ^ = 0.48 SSE=1.843,\hat\sigma=0.48 SSE=1.843,σ^=0.48
(5)给出 β ^ 0 \hat\beta_0 β^0与 β ^ 1 \hat\beta_1 β^1的置信度为95%的区间估计
5.1问题分析
β
^
1
\hat\beta_1
β^1与
β
^
0
\hat\beta_0
β^0的分布为
β
^
1
∼
N
(
β
1
,
σ
2
L
x
x
)
,
β
^
0
∼
N
(
β
0
,
[
1
n
+
x
ˉ
2
L
x
x
]
σ
2
)
\hat\beta_1\sim{N\left(\beta_1,\frac{\sigma^2}{L_{xx}}\right)} , \quad \hat\beta_0\sim{N\left(\beta_0,\left[\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}}\right]\sigma^2\right)}
β^1∼N(β1,Lxxσ2),β^0∼N(β0,[n1+Lxxxˉ2]σ2)
由
β
^
1
\hat\beta_1
β^1分布构造了服从自由度为
n
−
2
n-2
n−2的
t
t
t分布统计量
t
=
(
β
^
1
−
β
1
)
L
x
x
σ
^
t=\frac{(\hat\beta_1-\beta_1)\sqrt{L_{xx}}}{\hat\sigma}
t=σ^(β^1−β1)Lxx
因而
P
(
∣
(
β
^
1
−
β
1
)
L
x
x
σ
^
∣
>
t
α
/
2
(
n
−
2
)
)
P\left(\left|\frac{(\hat\beta_1-\beta_1)\sqrt{L_xx}}{\hat\sigma}\right|>t_{\alpha/2}\left(n-2\right)\right)
P(∣
∣σ^(β^1−β1)Lxx∣
∣>tα/2(n−2))
得到
β
1
\beta_1
β1的置信度为
1
−
α
1-\alpha
1−α的置信区间为(
α
=
0.05
\alpha=0.05
α=0.05)
(
β
^
1
−
t
α
/
2
σ
^
L
x
x
,
β
^
1
+
t
α
/
2
σ
^
L
x
x
)
\left( \hat\beta_1-t_{\alpha/2}\frac{\hat\sigma}{\sqrt{L_{xx}}}, \hat\beta_1+t_{\alpha/2}\frac{\hat\sigma}{\sqrt{L_{xx}}} \right)
(β^1−tα/2Lxxσ^,β^1+tα/2Lxxσ^)
对
β
^
0
\hat\beta_0
β^0同理得置信度为
1
−
α
1-\alpha
1−α的置信区间为(
α
=
0.05
\alpha=0.05
α=0.05)
(
β
^
1
−
t
α
/
2
[
1
n
+
x
ˉ
2
L
x
x
]
σ
^
,
β
^
1
+
t
α
/
2
[
1
n
+
x
ˉ
2
L
x
x
]
σ
^
)
\left( \hat\beta_1-t_{\alpha/2}\sqrt{\left[\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}}\right]}\hat\sigma, \hat\beta_1+t_{\alpha/2}\sqrt{\left[\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}}\right]}\hat\sigma \right)
(β^1−tα/2[n1+Lxxxˉ2]σ^,β^1+tα/2[n1+Lxxxˉ2]σ^)
5.2问题求解
5.2.1输入
alpha<-0.05 #置信度
#beta_0,beta_1的分布标准差
sd.beta_0<-sqrt((1/n+(meanx^2)/lxx))*sigma_hat
sd.beta_1<-sqrt(sigma_hat^2/lxx)
beta_1l<-beta_1-qt(1-alpha/2,n-2)*sd.beta_1#beta_1置信下限
beta_1u<-beta_1+qt(1-alpha/2,n-2)*sd.beta_1#beta_1置信上限
beta_0l<-beta_0-qt(1-alpha/2,n-2)*sd.beta_0#beta_0置信下限
beta_0u<-beta_0+qt(1-alpha/2,n-2)*sd.beta_0#beta_0置信上限
5.2.2输出
得到 β 1 \beta_1 β1的置信度为0.05的置信区间为 [ 0.0026 , 0.0046 ] \left[0.0026,0.0046 \right] [0.0026,0.0046]
得到 β 1 \beta_1 β1的置信度为0.05的置信区间为[-0.7,0.937]
(6) x x x与 y y y的决定系数
6.1问题分析
各平方和如下:
S
S
E
=
Σ
(
y
i
−
y
^
)
2
SSE=\Sigma(y_i-\hat{y})^2
SSE=Σ(yi−y^)2
S S R = Σ ( y ^ − y ˉ ) 2 SSR=\Sigma(\hat{y}-\bar{y})^2 SSR=Σ(y^−yˉ)2
S S T = S S R + S S E SST=SSR+SSE SST=SSR+SSE
决定系数为
r
2
=
S
S
R
S
S
T
r^2=\frac{SSR}{SST}
r2=SSTSSR
6.2问题求解
6.2.1输入
sse<-sum((y_hat-y)^2)#残差平方和
ssr<-sum((y_hat-meany)^2)#回归平方和
sst<-ssr+sse#总离差平方和
#计算xy决定系数
R<-ssr/sst
6.2.2输出
S S E = 1.84 , S S R = 16.68 , S S T = 18.525 , r 2 = 0.9 SSE=1.84,SSR=16.68,SST=18.525,r^2=0.9 SSE=1.84,SSR=16.68,SST=18.525,r2=0.9
(7)对回归方程做方差分析
7.1问题求解
7.1.1输入
f<-(ssr/1)/(sse/(n-2))
p1<-pf(f,1,n-2)#F为统计量、1为第一个自由度,n-2为第二个自由度
#1-p1为p值
7.2.2输出
一元线性回归方差分析表如下:
| 方差来源 | 自由度 | 平方和 | 均方 | F F F值 | P P P值 |
|---|---|---|---|---|---|
| 回归 | 1 | S S R = 16.68 SSR=16.68 SSR=16.68 | S S R / 1 = 16.68 SSR/1=16.68 SSR/1=16.68 | S S R / 1 S S E ( n − 2 ) = 72.40 \frac{SSR/1}{SSE(n-2)}=72.40 SSE(n−2)SSR/1=72.40 | p = 2.8 ∗ 1 0 − 5 p=2.8*10^{-5} p=2.8∗10−5 |
| 残差 | n − 2 n-2 n−2 | S S E = 1.84 SSE=1.84 SSE=1.84 | S S E / ( n − 2 ) = 0.23 SSE/(n-2)=0.23 SSE/(n−2)=0.23 | ||
| 总和 | n − 1 n-1 n−1 | S S T = 18.525 SST=18.525 SST=18.525 |
(8)做回归系数 β 1 \beta_1 β1的显著性检验
8.1问题分析
β
^
1
\hat\beta_1
β^1的分布为
β
^
1
∼
N
(
β
1
,
σ
2
L
x
x
)
\hat\beta_1\sim{N\left(\beta_1,\frac{\sigma^2}{L_{xx}}\right)}
β^1∼N(β1,Lxxσ2)
假设检验原假设为
H
0
:
β
1
=
0
H_0:\beta_1=0
H0:β1=0 ,构造检验统计量
t
t
t服从自由度为
n
−
2
n-2
n−2 的
t
t
t 分布
t
=
β
^
1
L
x
x
σ
^
t=\frac{\hat\beta_1\sqrt{L_{xx}}}{\hat\sigma}
t=σ^β^1Lxx
并计算对应的
p
p
p 值
8.2问题求解
8.2.1输入
#回归系数的beta_1的t检验
t1<-beta_1/sd.beta_1 #t统计量
p2<-pt(t1,n-2) #(1-p2)为p值
8.2.2输出
t = 8.50 , p = 1.40 ∗ 1 0 − 5 t=8.50,p=1.40*10^{-5} t=8.50,p=1.40∗10−5
(9)做相关系数的显著性检验
9.1问题分析
相关系数为
r
r
r
r
=
L
x
y
L
x
x
L
y
y
=
β
^
1
L
x
x
L
y
y
r=\frac{L_{xy}}{\sqrt{L_{xx}L_{yy}}}=\hat\beta_1\sqrt{\frac{L_{xx}}{L_{yy}}}
r=LxxLyyLxy=β^1LyyLxx
构造检验统计量
t
=
n
−
2
r
1
−
r
2
∼
t
(
n
−
2
)
t=\frac{{\sqrt{n-2}}{r}}{\sqrt{1-r^2}}\sim{t(n-2)}
t=1−r2n−2r∼t(n−2)
当
∣
t
∣
>
t
α
/
2
(
n
−
2
)
\vert{t}\vert>t_{\alpha/2}(n-2)
∣t∣>tα/2(n−2) 时,认为简单回归系数显著不为零
9.2问题求解
9.2.1输入
#相关系数r的t检验
r<-lxy/(sqrt(lxx*lyy))
t2<-sqrt(n-2)*r/sqrt(1-r^2);
p3<-pt(t2,n-2) #(1-p3)为p值
9.2.2输出
t = 8.50 , p = 1.40 ∗ 1 0 − 5 t=8.50,p=1.40*10^{-5} t=8.50,p=1.40∗10−5
(10)对回归方程作残差图并做相应的分析
10.1问题求解
10.1.1输入
#残差图
# screen(3)
e<-y_hat-y #残差
n<-length(e)
sigma_u<-seq(2*sigma_hat,2*sigma_hat,length.out=n) #残差2σ原则
sigma_l<-seq(-2*sigma_hat,-2*sigma_hat,length.out=n)
plot(x,e,ylim=c(5,-5))
points(x,sigma_u,type="l") #画2σ上下界
points(x,sigma_l,type="l")
title(main="残差图")
10.1.2输出

10.2问题分析
计算出残差后,及自变量x为横轴,以残差为总纵轴画散点图得到残差图,从残差图上看出,产茶时围绕着 e = 0 e=0 e=0 随机波动,并且波动范围在方差估计 σ ^ \hat\sigma σ^的两倍。所以可以判定模型的基本假定是满足的。
(11)该公司预计下一周签发新保单 x 0 = 1000 x_0=1000 x0=1000张,需要的加班时间时多少?
11.1问题求解
11.1.1输入
x0<-1000
y0<-beta_0+beta_1*x0
11.1.2输出
y = 3.7 y=3.7 y=3.7
(12)给出 y 0 y_0 y0的置信度为95%的精确预测区间和近似预测区间
12.1问题分析
可以计算得到
y
^
0
\hat{y}_0
y^0 的分布为
y
^
0
∼
N
(
β
0
+
β
1
x
0
,
(
1
n
+
(
x
0
−
x
ˉ
)
2
L
x
x
)
σ
2
)
\hat{y}_0\sim N\left( \beta_0+\beta_1x_0,(\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}})\sigma^2\right)
y^0∼N(β0+β1x0,(n1+Lxx(x0−xˉ)2)σ2)
所以枢轴量为
y
0
−
y
^
0
∼
N
(
0
,
(
1
+
h
00
)
σ
2
)
,
h
00
=
(
1
n
+
(
x
0
−
x
ˉ
)
2
L
x
x
)
y_0-\hat{y}_0\sim N\left(0,(1+h_{00})\sigma^2\right),h_{00}=(\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}})
y0−y^0∼N(0,(1+h00)σ2),h00=(n1+Lxx(x0−xˉ)2)
统计量为
t
=
y
0
−
y
0
^
1
+
h
00
σ
^
∼
t
(
n
−
2
)
t=\frac{y_0-\hat{y_0}}{\sqrt{1+h_{00}}\hat\sigma}\sim t(n-2)
t=1+h00σ^y0−y0^∼t(n−2)
得精确置信区间为
y
0
^
±
t
α
/
2
(
n
−
2
)
1
+
h
00
σ
^
\hat{y_0} \pm t_{\alpha/2}(n-2)\sqrt{1+h_{00}}\hat\sigma
y0^±tα/2(n−2)1+h00σ^
近似预测区间为
y
^
0
±
2
σ
^
\hat{y}_0\pm2\hat\sigma
y^0±2σ^
12.2问题求解
12.2.1输入
#因变量新值95%置信区间
h00<-1/n+((x0-meanx)^2)/lxx
y0_l<-y0-qt(1-alpha/2,n-2)*sqrt(1+h00)*sigma_hat#预测新值得置信下限
y0_u<-y0+qt(1-alpha/2,n-2)*sqrt(1+h00)*sigma_hat#预测新值得置信上限
12.2.2输出
精确置信区间为[2.519,4.887]
近似预测区间为[2.743,4.663]
所以两区间比较接近,可以用近似区间估计
(13)给出 E ( y 0 ) E(y_0) E(y0)的置信度为95%的区间估计
13.1问题分析
根据
y
^
0
\hat{y}_0
y^0 构造枢轴量(含
E
(
y
0
)
E(y_0)
E(y0))
y
0
^
−
E
(
y
0
)
∼
N
(
0
,
h
00
σ
2
)
,
h
00
=
(
1
n
+
(
x
0
−
x
ˉ
)
2
L
x
x
)
\hat{y_0}-E({y}_0)\sim N\left(0,h_{00}\sigma^2\right),h_{00}=(\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}})
y0^−E(y0)∼N(0,h00σ2),h00=(n1+Lxx(x0−xˉ)2)
统计量为
t
=
y
0
−
y
0
^
h
00
σ
^
∼
t
(
n
−
2
)
t=\frac{y_0-\hat{y_0}}{\sqrt{h_{00}}\hat\sigma}\sim t(n-2)
t=h00σ^y0−y0^∼t(n−2)
得置信水平95%得精确置信区间为
y
0
^
±
t
α
/
2
(
n
−
2
)
h
00
σ
^
\hat{y_0} \pm t_{\alpha/2}(n-2)\sqrt{h_{00}}\hat\sigma
y0^±tα/2(n−2)h00σ^
13.2问题求解
13.2.1输入
#因变量新值得平均值的95%置信区间
y0_l_E<-y0-qt(1-alpha/2,n-2)*sqrt(h00)*sigma_hat#预测新值均值得置信下限
y0_u_E<-y0+qt(1-alpha/2,n-2)*sqrt(h00)*sigma_hat#预测新值均值得置信上限
13.2.2输出
E ( y 0 ) E(y_0) E(y0)的95%置信区间为[3.283,4.122]
例题2.1(火灾)
(1)问题求解
根据上一题的程序,我们对例题2.1直接求解
1.1输入
setwd("E:/AllClass/junior1/RegressionAnalysis/unit2")#设置文件路径
#保留原路径setwd("C:/User/10854/documents")
#以下利用理论方法使用一元回归模型
#导入数据
data<-read.csv("2-1.csv")#书本火灾题目,表数据2-1
x<-data[,1];y<-data[,2]
n<-length(x)
split.screen(c(1,3))
screen(1)
plot(x,y)
title(main="数据散点图")
#求均值与回归变量lxx,lyy,lxy
meanx<-mean(x);meany<-mean(y)
lxx<-sum((x-meanx)^2)
lyy<-sum((y-meany)^2)
lxy<-sum((x-meanx)*(y-meany))
#回归系数估计
beta_1<-lxy/lxx#beta_1
beta_0<-meany-beta_1*meanx#beta_0
screen(2)
plot(x,y)
points(x,beta_0+beta_1*x,type="l")
title(main="回归图")
#预测值与平方和
y_hat<-beta_0+beta_1*x
sse<-sum((y_hat-y)^2)#残差平方和
ssr<-sum((y_hat-meany)^2)#回归平方和
sst<-ssr+sse#总离差平方和
#回归误差ε的方差sigma估计
sigma_hat<-sqrt(1/(n-2)*sse)
#对bet_0、beta_1的95%区间估计
alpha<-0.05
#beta_0,beta_1的分布标准差
sd.beta_0<-sqrt((1/n+(meanx^2)/lxx))*sigma_hat
sd.beta_1<-sqrt(sigma_hat^2/lxx)
beta_1l<-beta_1-qt(1-alpha/2,n-2)*sd.beta_1#beta_1置信下限
beta_1u<-beta_1+qt(1-alpha/2,n-2)*sd.beta_1#beta_1置信上限
beta_0l<-beta_0-qt(1-alpha/2,n-2)*sd.beta_0#beta_0置信下限
beta_0u<-beta_0+qt(1-alpha/2,n-2)*sd.beta_0#beta_0置信上限
#计算xy决定系数
R<-ssr/sst
#回归方程的显著性检验
#方差分析F检验
f<-(ssr/1)/(sse/(n-2))
p1<-pf(f,1,n-2)#F为统计量、1为第一个自由度,n-2为第二个自由度
#回归系数的beta_1的t检验
t1<-beta_1/sd.beta_1#t统计量
p2<-pt(t1,n-2)
#残差图
screen(3)
e<-y_hat-y
n<-length(e)
sigma_u<-seq(2*sigma_hat,2*sigma_hat,length.out=n)#残差2σ原则
sigma_l<-seq(-2*sigma_hat,-2*sigma_hat,length.out=n)
plot(x,e,ylim=c(12,-12))
points(x,sigma_u,type="l")
points(x,sigma_l,type="l")
title(main="残差图")
1.2输出
回归方程如下
y
i
=
10.28
+
4.91
x
i
y_i=10.28+4.91x_i
yi=10.28+4.91xi
参数表如下:
| 参数 | 参数值 |
|---|---|
| β ^ 0 \hat\beta_0 β^0 | 10.28 |
| β ^ 1 \hat\beta_1 β^1 | 4.91 |
| r 2 r^2 r2 | 0.92 |
| σ ^ \hat\sigma σ^ | 2.31 |
| β ^ 0 区间估计 \hat\beta_0区间估计 β^0区间估计 | [7.2,13.34] |
| β ^ 1 区间估计 \hat\beta_1区间估计 β^1区间估计 | [4.07,5.76] |
| 一元线性回归方差分析表如下: |
| 方差来源 | 自由度 | 平方和 | 均方 | F F F值 | P P P值 |
|---|---|---|---|---|---|
| 回归 | 1 | S S R = 841.8 SSR=841.8 SSR=841.8 | S S R / 1 = 841.8 SSR/1=841.8 SSR/1=841.8 | S S R / 1 S S E / 13 = 156.89 \frac{SSR/1}{SSE/13}=156.89 SSE/13SSR/1=156.89 | p = 1.248 ∗ 1 0 − 8 p=1.248*10^{-8} p=1.248∗10−8 |
| 残差 | 13 13 13 | S S E = 69.8 SSE=69.8 SSE=69.8 | S S E / 13 = 5.37 SSE/13=5.37 SSE/13=5.37 | ||
| 总和 | 14 14 14 | S S T = 911.5 SST=911.5 SST=911.5 |
回归方程的 β ^ 1 \hat\beta_1 β^1的检验中, p p p值为 6.239 ∗ 1 0 − 9 < 0.05 6.239 *10^{-9}<0.05 6.239∗10−9<0.05
数据的散点图,回归图,残差图如下
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZPFVwi2s-1570342114068)(C:\Users\10854\AppData\Roaming\Typora\typora-user-images\1570338668192.png)]](https://i-blog.csdnimg.cn/blog_migrate/266d911d427f9e488600f30acfa542c4.png)
(2)结果分析
因为决定系数为0.92,具有比较强的线性相关性,且残差均在 ± 2 σ ^ \pm2\hat\sigma ±2σ^ 内波动,而线性回归系数 β ^ 1 \hat\beta_1 β^1的检验通过,所以可以认为火灾发生地点与最近的消防站距离和火灾损失呈线性关系,符合模型 y i = 10.28 + 4.91 x i y_i=10.28+4.91x_i yi=10.28+4.91xi
数据与源代码链接
链接: https://pan.baidu.com/s/1hYTp5mc5nmtSBzq9GSBBfQ?pwd=6666
提取码:6666








 本文详细解析了一元线性回归的实际应用,包括散点图绘制、回归方程求解、标准误差估计、置信区间计算、决定系数分析、方差分析、显著性检验、残差图解读及预测区间估计,提供了丰富的案例分析。
本文详细解析了一元线性回归的实际应用,包括散点图绘制、回归方程求解、标准误差估计、置信区间计算、决定系数分析、方差分析、显著性检验、残差图解读及预测区间估计,提供了丰富的案例分析。
















 176
176

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








