简单货机装运模型lingo求解

线性规划

lingo重点：集合语言：

题目如下：

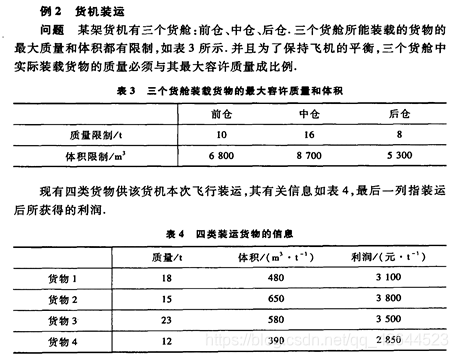
一、集合段

• 集合一：cang表示有三个仓库
• 集合二：wu表示有四个货物
• 集合三：link(wu,cang) 是wu四个元素/cang三个元素形成的矩阵集合

WET：每个cang的限重量
VOL：每个cang的限空间
w：每个wu的质量上限
v：每个wu的密度倒数
p：每个wu的利润
x(ij)：第i个wu运输到第j个cang的质量

!【集合段】定义集合及变量;
sets: 
	cang/1..3/:WET,VOL;
	wu/1..4/:w,v,p;
	link(wu,cang):x;
endsets

二、数据段

对每个向量进行赋值货物 i=1234代表四个货物, 货舱 j=123表示前中后舱

!【数据段】对已知变量赋值;
data: 
	WET=10,16,8; VOL=6800,8700,5300; 
	w=18,15,23,12; v=480,650, 580,390; 
	p=3100,3800,3500,2850;
enddata

三、目标函数约束段

目标函数
$$maxz={\Sigma }^{i}p(i)({\Sigma }^{j}x(ij))$$
四种货物总质量约束
$${\Sigma }^{j}x(ij)\le w(i),i=1,2,3,4$$
三货舱质量限制
$${\Sigma }^{i}x(ij)\le WET(j),j=1,2,3$$
三货舱空间限制
$${\Sigma }^{i}v(i)x(ij)\le VOL(j),j=1,2,3$$
三个货舱装入质量的平衡约束
（互不相等且必须两两比较用该式代码）
$$\Sigma x(ij)/WET(j)=\Sigma x(ik)/WET(k),j,k=1,2,3;j̸=k$$
对于Σ使用sum函数自然遍历下标，对于满足好几个相似的式子如上

max=@sum(wu(i):p(i)*@sum(cang(j):x(i,j)));
@for(wu(i):@sum(cang(j):x(i,j))<w(i));
@for(cang(j):@sum(wu(i):x(i,j))<WET(j));
@for(cang(j):@sum(wu(i):v(i)*x(i,j))<VOL(j));
@for(cang(j):
	@for(cang(k)|k #GT# j:	!#GT#是大于等于的含义;
		@sum(wu(i):x(i,j)/WET(j))=@sum(wu(i):x(i,k)/WET(k)));
);
END