机械学习 - 数学基础 - 1

前言

学了这个，需要记忆不只是理论，还有里面各种术语的各种别名，容易被绕晕，不弄明白就会像路痴似的，找不到思维迷宫的出口。
笔者的文章有点随心所欲，能够接受的就请看下去，不能接受的，请另请高明。

涉及课程：线性代数、离散数学、概率论、统计学

测试环境：（请注意这里是虚拟环境 Virtualenv）

操作系统： Window 10
工具：Pycharm
Python: 3.7
scikit-learn: 1.0.2
numpy: 1.21.6
scipy: 1.7.3
threadpoolctl: 3.1.0
joblib: 1.1.0

大致运行环境知道就行了，这里主要介绍数学基础，但是笔者会和python的一些实操混合，毕竟后面要用python实现机械学习，甚至是深度学习等等。

一、数学基础

• 点——标量（scalar）
• 线——向量（vector）
• 面——矩阵（matrix）
• 体——张量（tensor）

线性代数

标量（scalar）

1. 标量（scalar），亦称“无向量”。有些物理量，只具有数值大小，而没有方向，部分有正负之分。物理学中，标量（或作纯量）指在坐标变换下保持不变的物理量。用通俗的说法，标量是只有大小，没有方向的量；
2. 有些物理量，只具有数值大小，而没有方向，部分有正负之分。这些量之间的运算遵循一般的代数法则，称做“标量”。如质量、密度、温度、功、能量、路程、速率、体积、时间、热量、电阻、功率、势能、引力势能、电势能等物理量。无论选取什么坐标系，标量的数值恒保持不变。
3. 矢量和标量的乘积仍为矢量。标量和标量的乘积仍为标量。矢量和矢量的乘积，可构成新的标量，也可构成新的矢量，构成标量的乘积叫标积；构成矢量的乘积叫矢积
4. 物理学中，标量（或作纯量）指在坐标变换下保持不变的物理量。例如，欧几里得空间中两点间的距离在坐标变换下保持不变，相对论四维时空中时空间隔在坐标变换下保持不变。以此相对的矢量，其分量在不同的坐标系中有不同的值，例如速度。
5. 物理学上常见的矢量、标量举例：
   ①矢量：力（包括力学中的"力"和电学中的"力"），力矩、线速度、角速度、位移、加速度、动量、冲量、角动量、场强等 　
   ②标量：质量、密度、温度、功、功率、动能、势能、引力势能、电势能、路程、速率、体积、时间、热量、电阻等标量正负的意义

有的标量用正负来表示大小，如重力势能、电势；
有的标量用正负来表示性质，如电荷量，正电荷表示物体带正电，负电荷表示物体带负电
有的标量用正负来表示趋向，如功，功的正负表示能量转化的趋向，力对物体做正功，物体的动能增加（增加趋向），若力对物体做负功，则物体的动能减小（减小趋向）。
标量的正负只代表大小，与方向无关。
注意：标量不遵守平行四边形法则！

向量 (vector)

1. 在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向；

2. 在物理学和工程学中，几何向量更常被称为矢量。许多物理量都是矢量，比如一个物体的位移，球撞向墙而对其施加的力等等。与之相对的是标量，即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系，例如向量势对应于物理中的势能。(势能明明是作为标量，但为什么会被对应为向量势，这句话我理解为由于无限的向量指向无限的方向，那么这时的所有向量便组成了一个向量势，由此势能就被定义为没有方向，只有大小的标量)；

3. 代数表示
   表示向量的符号，头上加一个箭头，比如a 头上加箭头，便是向量 $\vec{a}$；

4. 几何表示
   向量可以用有向线段来表示。有向线段的长度表示向量的大小，向量的大小，也就是向量的长度。箭头所指的方向表示向量的方向。(既然是线段，那么就一定是有端点的，不能无限延伸，会有终点)
   长度为0的向量叫做零向量；
   长度等于1个单位的向量，叫做单位向量；

5. 坐标表示
   由平面向量基本定理可知，有且只有一对实数（x,y），使得a=xi+yj，因此把实数对(x,y)叫做向量 $\vec{a}$ 的坐标，记作a=(x,y)。这就是向量 $\vec{a}$ 的坐标表示。其中(x,y)就是点 的坐标。向量 $\vec{a}$ 称为点P的位置向量。
   由空间基本定理知，有且只有一组实数$(x,y,z)$，使得 $a=ix+jy+kz$，因此把实数对$(x,y,z)$叫做向量 $\vec{a}$ 的坐标，记作a=(x,y,z)。这就是向量a的坐标表示。其中$(x,y,z)$，就是点P的坐标。向量a称为点P的位置向量。

6. 矩阵表示: $a=\left|\begin{array}{c}x\\ y\end{array}\right|,二维矩阵；$ $a=\left|\begin{array}{c}x\\ y\\ z\end{array}\right|，三维矩阵$
   矩阵使用大方括号 $[]$ 括起来的，不过这里矩阵只能如此表示，只要注意这一点就可以了。

7. 向量空间分为二维向量空间、三维向量空间…n维向量空间，向量即矢量；

参考链接：
向量

矩阵 (matrix)

1. 矩阵：

矩阵参考链接：

• 矩阵
• 什么是矩阵的模

2. 只有方阵才能是矩阵，否则不是矩阵；

3. 矩阵可以看做是多个向量组合的向量空间；

4. 矩阵行列式计算：

行列式参考链接：

• 行列式

• 二阶行列式

• 行列式的计算方法(含四种，看完就会！)

• 线性代数知识汇总_行列式

7. python使用模块 numpy ，通过创建二维数组(这里的二维数组其实是列表数据类型表示的[[ ]])，代码如下所示：

import numpy
n=numpy.array(([12,54,94,51,26],[48,98,57,28,33],[58,97,64,23,58]))
print(n)

运行结果：

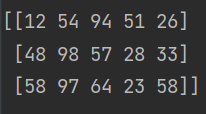
这表示3行5列的矩阵，而且通过类似数组的方法，可以对 n 的内容进行更新赋值，如 n[0][0] = 100 ，就能够对其内的12 改变为100

结果：

参考链接：
如何使用python表示矩阵

参考链接：
AI 知识库 数学基础

范数(norm) —— 与向量、矩阵的关联

2. 范数，是具有“长度”概念的函数；
3. 在线性代数、泛函分析及相关的数学领域，范数是一个函数，是矢量(向量)空间内的所有矢量赋予非零的正长度或大小；
4. 半范数可以为非零的矢量(向量)赋予零长度；
5. 范数常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。
6. 定义范数的矢量空间是赋范矢量空间；

注：在二维的欧氏几何空间R中定义欧氏范数，在该矢量空间中，元素被画成一个从原点出发的带有箭头的有向线段，每一个矢量的有向线段的长度即为该矢量的欧氏范数。

总结：在一个二维空间内，以原点 O 为起始点的任意一个向量的长度，是该向量的范数。—— 也称之为欧氏范数

5. 半范数
   假设 $V$是域 $F$ 上的矢量空间，$V$ 的半范数是一个函数 $P:V\to R，x\to P(x)，$ 满足：
   $\forall a\in F，\forall u,v\in V$

• $p(v)⩾0$ （非负性）

• $P(av)=|a|P(v)$ （正值齐次性）

• $P(u+v)⩽P(u)+P(v)$ (三角不等式).

• 范数 = 半范数 + 额外性质

分析：
先解释一番域是什么，总结一句，无论是实数集R、复数集C、有理数集Q等等，只要是满足了某种特征公式的 n个数，该 n个数能够完成 $+-\times ÷$ 等四则运算的的数组成了一个域，就说域是封闭，且n可以是无穷多个数，也可以是有限个数(有限域，n $⩾2$)。
域的参考链接：初等数论入门：什么是“域”
数域的参考链接(有兴趣的可以看下)：数域

$V$ 映射实数范围(有理数、无理数)，所以 $P(x)$ 内的 $x$ 是在实数范围内的数；

由于是范数是长度概念，那么就绝对不可能是负数 ($-$)；

$P(av)=|a|P(v)$ ，由于 $\forall a\in F$ (意味着在域$F$内，包括了矢量空间$V$内的任意 $a$)，所以 $a$ 和 $v$ 同时发生的情况，等于绝对值 $a$ ，即$|a|$ ，去乘$\times P(v)$，即 $|a|$ 倍的半范数 $P(v)$;

额外性质，应该是 $P(u+v)⩽P(u)+P(v)$ (三角不等式). 这里的原因，小于等于，那是否可以猜测是额外性质导致的差别。

6. 范数按类型分，可以分为向量范数和矩阵范数，向量组成了矩阵，所以可以思考向量的范数与矩阵的范数之间的关系；
7. 向量范数

总的来说，范数的本质是距离，存在的意义是为了实现比较。比如，在一维实数集合中，我们随便取两个点4和9，我们知道9比4大，但是到了二维实数空间中，取两个点（1，1）和（0，3），这个时候我们就没办法比较它们之间的大小，因为它们不是可以比较的实数，于是我们引入范数这个概念，把我们的（1，1）和（0，3）通过范数分别映射到实数$\sqrt{2}$和 3 ，这样我们就比较这两个点了。所以你可以看到，范数它其实是一个函数，它把不能比较的向量转换成可以比较的实数。
在上面的例子里，我们用的范数是平方求和然后再开方，即向量的 2 - 范数，而且范数还有很多其他的类型，这个就要看具体的定义了，理论上我们也可以把范数定义为只比较x轴上数字的绝对值之和，也就是向量的 1 - 范数。
PS：我这里说的是向量范数。😉

1 - 范数 2 - 范数也是可以用来度量一个整体，比如两个个班的人比较高度，你可以用班里面最高的人（无穷范数 $\propto$）去比较，也可以用班里所有人的身高总和比较（1 - 范数），也可以求平均（几何平均？忘记了。。）（类似2 - 范数）。
举一个简单的例子，一个二维度的欧氏几何空间 $R^2$就有欧氏范数。在这个向量空间的元素（譬如：$(3,7)$）常常在笛卡儿坐标系统被画成一个从原点出发的箭号。每一个向量的欧氏范数就是箭号的长度，也就是勾股定理，$c^2=a^2+b^2$。

公式：
假设有一个向量 $\overrightarrow{a_1}$，求其范数，但是这里将向量范数分为了 4 种范数，如下所示：

• 向量的 0范数，向量中非零元素的个数。

• 向量的 1 - 范数，为所有输入值x的绝对值之和。

• 向量的 2 - 范数，就是通常意义上的模。 便是求向量 $\overrightarrow{a_1}$ 的模长 $||a_1||$，所有输入值x的平方之和

• 向量的 无穷范数，就是取向量内所有输入值x的绝对值后的最大值。

公式如下：

向量的 1 - 范数：将向量内所有的元素，先绝对值化，然后相加

向量的 2 - 范数：将向量内所有的元素，先绝对值化，然后每一个都平方后相加，再开平方 $\sqrt{x}$

向量的 p - 范数：将向量内所有的元素，先绝对值化，然后每一个都 p 方后相加，再开p方 $\sqrt[p]{x}$

向量的无穷范数：找到向量内所有元素中绝对值最大的一个元素，作为范数

7. 矩阵的模，又称为范数，比如 $||A||$，指的是 矩阵 $A$ 的模长。
8. 矩阵范数

• 矩阵的 1 - 范数： 为每一列/行绝对值之和的最大值，即特征向量的绝对值之和的最大值。，通常是按列计算，即一列便是一个特征向量。
• 矩阵的 2 - 范数公式：
  $||A||=\sqrt{\lambda (A_{}^{T}A)}$ 称为 A 的 2 - 范数，$||A||$ 代表了矩阵 $A$ 的长度，$||A||$ 也被称作矩阵 $A$ 的模长

其中$\lambda (A_{}^{T}A)$ 为 $A_{}^{T}A$ 的特征值的绝对值的最大值

总结：

1. 矩阵的范数，通过矩阵这个映射，可以把一个集合映射为另外的一个集合，通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例，所谓的特例，是在1、2、3维空间内，函数是一个可以被人具象化理解的。

2. 当函数与几何超出三维空间时，就难以获得较好的想象，于是就有了映射的概念，为了更好的在数学上表达这种映射关系，（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。而通过向量来表示上述映射中所说的这个集合，而我们通常所说的基，就是这个集合的最一般的关系。
   于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另外一个几何（另外一个向量）。

3. 对于矩阵和向量，其实我们一直会把多个向量组合形成一个矩阵，比如 $\overrightarrow{a_1}$ 、$\overrightarrow{a_2}$、$\overrightarrow{a_3}$…$\overrightarrow{a_n}$，如果都清楚向量的矩阵模式，就应该清楚，同行同列的向量是可以组合成一个方阵，即矩阵，如$X=\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|$ $\overrightarrow{a_1}=\left|\begin{array}{c}{a}_{11}\\ a_{21}\\ a_{31}\end{array}\right|$ $\overrightarrow{a_2}=\left|\begin{array}{c}{a}_{12}\\ a_{22}\\ a_{32}\end{array}\right|$ $\overrightarrow{a_3}=\left|\begin{array}{c}{a}_{13}\\ a_{23}\\ a_{33}\end{array}\right|$

4. 向量的范数，就是表示这个原有集合的大小，比如上面的向量$\overrightarrow{a_1}$、$\overrightarrow{a_2}$、$\overrightarrow{a_3}$ 等分别就是一个集合。
   矩阵的范数，就是表示这个变化过程的大小的一个度量。

5. 一个矩阵范数往往由一个向量范数引出，我们称之为算子范数，也就是得出最大的一个范数，从这句话可以知道，其实矩阵的范数，不是唯一的，比如从特征向量$\overrightarrow{a_1}$、$\overrightarrow{a_2}$、$\overrightarrow{a_3}$ 中找出最大的绝对值之和的向量范数，便是算子范数，这里的向量范数指的是特征向量的 1 - 范数，对于矩阵而言是列范数，如果是行范数，那么则是求矩阵的无穷范数；

公式：

通常，我们计算矩阵的范数，常用的是矩阵的 1 - 范数，即列范数，比较矩阵中所有的特征向量中 1 - 范数最大的一个向量 1 - 范数，作为矩阵的列范数 —— 1 - 范数 $||A|{|}_1$。 和列范数对应的是矩阵的无穷范数 —— 矩阵的行范数 、$\propto -范数$、$||A|{|}_{\propto }$ 。

参考链接：

计算方法 | 范数（向量：1范数、2范数、无穷范数；矩阵：行范数、列范数）

范数对于数学的意义？1范数、2范数、无穷范数

概率论与数理统计

随机变量（random variable）

1. 从数学观点来看，它们表现了同一种情况，这就是每个变量都可以随机地取得不同的数值，而在进行试验或测量之前，我们要预言这个变量将取得某个确定的数值是不可能的；（你不太可能有预知超能力，对吧？有的话，请低调，别搞事）
   (这里我们列出所有可能性结果，统称为随机变量 $X$，那么其中出现的一个结果是随机变量X的子集，比如一个硬币会有两种结果，正面和反面，那么这两种结果自然就是随机变量X的子集)

2. 按照随机变量可能取得的值，可以把它们分为两种基本类型：

① 离散型（discrete）随机变量（discrete random variable）

即在一定区间内变量取值为有限个或可数个。例如某地区某年人口的出生数、死亡数，某药治疗某病病人的有效数、无效数等。离散型随机变量通常依据概率质量函数分类，主要分为：伯努利随机变量、二项随机变量、几何随机变量和泊松随机变量

② 连续型（continuous）随机变量（continuous random variable）

即在一定区间内变量取值有无限个，或数值无法一一列举出来。例如某地区男性健康成人的身长值、体重值，一批传染性肝炎患者的血清转氨酶测定值等。有几个重要的连续随机变量常常出现在概率论中，如：均匀随机变量、指数随机变量、伽马随机变量和正态随机变量

所谓离散型，不过是对于整数型变量的整合，而连续型是对小数/浮点数变量的整合。

从上面的赌博的例子可以得知，赌博是一个离散型随机变量 $X$，那么其中变量输出值x1的可能出现的概率是一个可以大致知道的值，那么如果是连续型随机变量 $X$呢？这就会涉及到一个关于概率的密度函数的问题了，我们如何得知在一个区间内浮点数的概率，如果细化浮点数，我们可以得到无限个概率值，所以这就需要大致计算出概率分布于这个区间内的密度函数是多少。

离散型随机变量X的概率密度函数f(x)

针对于连续的随机变量的，与离散随机变量的期望值的算法同出一辙，由于输出值是连续的，所以把求和改成了积分

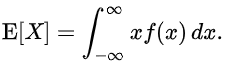
$f(x)$是概率密度函数，$x$是连续型随机变量的输出值，$dx$是微分

均值 (平均数)（mean value）

1. 资料链接：均值一般指平均数

期望值（expectation）

1. 是指在一个离散性随机变量试验中每次可能结果的概率乘以其结果的总和：
   ∑ p × X
p是X输出值的概率，X是输出值
2. 在概率论和统计学中，一个随机变量的期望值是变量的输出值乘以其机率的总和，换句话说，期望值是该变量输出值的平均数
   举例：
   美国赌场中经常用的轮盘上有38个数字，每一个数字被选中的几率都是相等的。赌注一般压在其中某一个数字上，如果轮盘的输出值和这个数字相等，那么下赌者可以将相当于赌注35倍的奖金和原赌注拿回（总共是原赌注的36倍），若输出值和下压数字不同，则赌注就输掉了。因此，如果赌注是1美元的话，这场赌博的期望值是：（这里所谓的一个随机变量，是包含了 -1 、35、1 这三个变量输出值，统称为随机变量 X = {-1, 35, 1}）
   
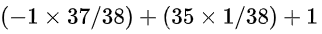
   结果是
   
   也就是说，平均起来每赌一次就会输掉0.053美元。
   分析：
   第一个是输了1美元，也就是 -1 × 37/38 ，选中了一个数，结果却是另外的 37 个数，便是输了，即 -1 ，第二个是赢了 35 块钱，不算本金 1美元，35 × 1/38，即选中了38位数之一，第三个是 1 ，即没有赌博，也就是不赌了，本金 1美元依旧在。

如果，赌注是n美元选n个数字的话，结果是：

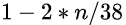
( -n × (38－n) / 38 ) + (35 × n × ( n/38 ) ) + n

3. 期望值并不一定包含于变量的输出值集合里;
4. 资料链接：期望值

笔者个人的期望值理解：

期望值是所有可能的结果与各自的结果概率相乘后的和，这个过程会有损失利益，也有获取利益的可能性，也有不作为的可能性，这些种种可能结果的和，便是每一场、每一次的平均结果，在这里只考虑经过了种种经历，最终只剩下的精粹还有多少，根据这一结果可以考虑具体的损失。

离均差平方和（sum of square,SS）

离均差平方和公式

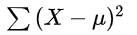
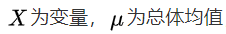
方差 （variance）

1. 统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数;

2. 平均离均差平方和公式（总体方差计算公式）：
   
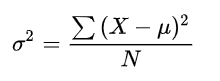
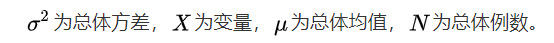
   实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：
   
   

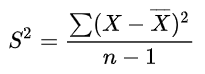
3. 概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度;

4. 方差是衡量源数据和期望值相差的度量值;

5. 方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程度的最重要的方法。

6. 标准差与方差不同的是，标准差和变量的计算单位相同，比方差清楚，因此很多时候我们分析的时候更多的使用的是标准差;

7. 方差 = 标准差的平方;

8. 资料链接：方差

标准差（standard deviation, std）

1. 由于方差是数据的平方，与检测值本身相差太大，人们难以直观的衡量，所以常用方差开根号换算回来这就是我们要说的标准差；

2. 标准差就是样本平均数方差的开平方 —— 也就是根号方差；

3. 标准差受到极值的影响。标准差越小，表明数据越聚集；标准差越大，表明数据越离散；

4. 标准差的大小因测验而定，如果一个测验是学术测验，标准差大，表示学生分数的离散程度大，更能够测量出学生的学业水平；如果一个测验测量的是某种心理品质，标准差小，表明所编写的题目是同质的，这时候的标准差小的更好；

5. 标准差与正态分布有密切联系：在正态分布中，1个标准差等于正态分布下曲线的68.26%的面积，1.96个标准差等于95%的面积。这在测验分数等值上有重要作用；

6. 资料链接：标准差

极差（range）

1. 最直接也是最简单的方法，即最大值(max)－最小值(min)（也就是极差）来评价一组数据的离散度。这一方法在日常生活中最为常见，比如比赛中去掉最高最低分就是极差的具体应用；

协方差（covariance, cov）

1. 协方差（Covariance）在概率论和统计学中用于衡量两个随机变量的总体误差；(下面的变量指的是随机变量)
2. 期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：
   
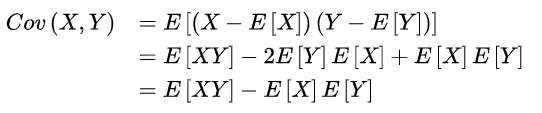
   对于这个公式的理解：

两个变量 $X$ 和 $Y$ 的离均差的积的期望值，即总体误差的平均数。
这里的离均差指的是误差，$X$ 随机变量与均值(期望值 $E[X]$)的误差大小，$Y$ 随机变量也是如此，两个变量的误差的叠加，即相乘 $\times$ ，便是元误差 —— 总体误差。
“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成

3. 方差是协方差的一种特殊情况，即当两个变量是相同的情况，也就是 $X=Y$，所以从上面的公式可以得知道，新公式如下：

$E[(X-E[X])\times (X-E[X])]=E[(X-E[X]{)}^2]$ ，方括号内是离均差平方,即离均差平方的期望值(平均数) ——方差,

5. 从直观上来看，协方差表示的是两个变量总体误差的期望；
6. 如果两个变量的变化趋势一致，即：
   ① 如果其中一个大于自身的期望值时，即 $X>E[X]$ 或 $Y>E[Y]$，另外一个也大于自身的期望值，即 $Y>E[Y]$ 或 $X>E[X]$，那么两个变量之间的协方差就是正值 $+$；
   ② 如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时 $X>E[X]$ 或 $Y>E[Y]$，另外一个却小于自身的期望值 $Y<E[Y]$ 或 $X<E[X]$，那么两个变量之间的协方差就是负值 $-$；
7. 如果 $X$ 与 $Y$ 是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足 $E[XY]=E[X]E[Y]$ ，但是，反过来并不成立。即如果 $X$ 与 $Y$ 的协方差为0，二者并不一定是统计独立的；
8. 协方差为0的两个随机变量称为是不相关的；
9. 协方差资料链接：协方差

协方差与方差的关系

$D(X)$ 指的是方差
$E(X)$指的是期望值

协方差与方差之间有如下关系：

$D(X+Y)=D(X)+D(Y)+2Cov(X，Y)$

$D(X-Y)=D(X)+D(Y)-2Cov(X，Y)$

由协方差定义，可以看出$Cov(X，X)=D(X)$，$Cov(Y，Y)=D(Y)$

协方差与期望值有如下关系：

$Cov(X，Y)=E(XY)-E(X)E(Y)$

意味着，需要计算两个变量总体误差的期望值，才能计算出协方差

协方差的性质：

（1）$Cov(X，Y)=Cov(Y，X)$；

（2）$Cov(aX，bY)=abCov(X，Y)，（a，b是常数）$；

（3）$Cov(X_1+X_2，Y)=Cov(X_1，Y)+Cov(X_2，Y)$;

（4）$Cov(X_1+a，Y+b)=Cov(X，Y)$

协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异

协方差的应用

1. 当两个变量相关时，用于评估它们因相关而产生的对应变量的影响；
2. 当多个变量独立时，用方差来评估这种影响的差异(一般是标准差，而不是方差)；
3. 当多个变量相关时，用协方差来评估这种影响的差异。

正态分布 (高斯分布)（normal distribution / Gaussian distribution）

别名：高斯分布、常态分布、钟形曲线

1. 若随机变量 $X$ 服从一个数学期望为 $\mu$、方差为 ${\sigma }^2$ 的正态分布，记为$N(\mu ，{\sigma }^2)$。其概率密度函数为正态分布的期望值 $\mu$ 决定了其位置，其标准差 $\sigma$ 决定了分布的幅度；
2. 当 $\mu =0,\sigma =1$时的正态分布是标准正态分布；

下一章节跳转链接

机械学习 - 基础概念 - scikit-learn - 数据预处理 - 1