Allan方差学习

一、遇到的问题

1. Allan deviation是什么？

有效地刻画了待研究的误差时间序列在不同时间尺度上的波动水平（不稳定性），并可根据不同时间尺度上的Allan方差值所构成的曲线的形状特征来辨识其中包含的随机过程模型

这就类似于我们用功率谱密度（PSD）来描述信号在不同频率尺度上的功率分布，并用PDS曲线来做系统模型辨识

2、和传统的误差分析有什么优势？

样本均值：反映整个误差序列有无宏观偏置（最简单的求平均数）

标准差STD：反映整个误差序列的波动情况(standard deviation)方差开根号，分母为什么是n-1?

是因为这样能使样本更好地逼近总体的标准差，保证方差的估计是无偏的。或者说：当我们使用样本来估计总体时，自由度就减一，所以是n-1.

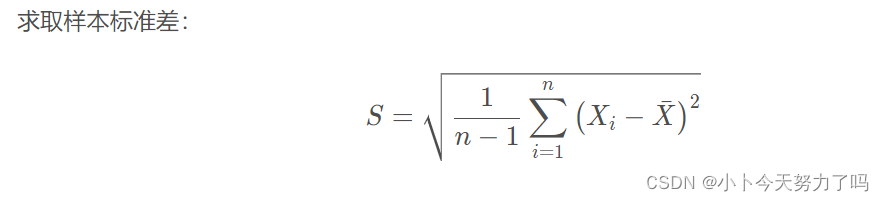
均方值根RMS：先平方、再平均、然后开方

它们都是反映误差序列的整体情况的指标，其中含有短时间快速变化和长时间缓变的各个成份，无法细分出不同时间尺度上的误差波动情况

(这个图有误，方差开根号是标准差）

3、如何得到Allan deviation?

Allan方差则是将误差序列在某个指定的时间尺度上的波动情况进行了精确提取，其具体计算步骤如下：

1. 将整段误差序列按照你感兴趣的时间尺度的长度（例如1分钟）进行分块；（这里有N块）
2. 每块求平均值；（将数据点求平均,消除小于关注时间长度的误差）
3. 相邻块的平均值求差；（消除大于时间长度的误差）
4. 将所有差值进行统计，得到其均方值，并乘以1/2。

 r 就是一分钟的分块      r0是分块里面更小的门时间，可以从图看的出来，这个门时间是拿来采样从而获取到了很多的数据点。

最后的到了一分钟这个时间长度的Allan偏差。

补充：如果我们只对某一时间尺度上的误差（即误差波动）感兴趣的话，那么比这个时间尺度更小的细节变化（短时间快速跳动）和比这个时间尺度更大的宏观变化（长时间缓慢漂移）就都不关心了，希望在我们的误差指标中都被消除掉。

而Allan方差是这样做到的：

1. 通过分块确定所要考察的时间块长度；
2. 利用块内求平均的办法把短于块长度的那些快速变化成份（细节）都抹掉；
3. 再利用相邻块求差的办法把长于两块长度的那些缓慢变化成份（宏观）都抹掉；
4. 最后对差值序列统计其均方值（这是处理任何随机样本的标准操作），这样统计出来的就是介于1倍块长度和2倍块长度这样一个很窄的时间尺度范围内的误差波动情况。

！！！如果我们对误差序列的各个时间尺度上的成份都感兴趣的话，可以将块长度由短到长，“扫描”一遍，得出一组Allan方差值，然后画个“Allan方差 vs. 块长度”的曲线，这样就能全面反映被研究的误差序列的特性了。具体的，实际上是“Allan方差的开方（Allan Deviation） vs. 块长度”的双对数曲线

 斜率为-1/2的直线段代表白噪声，按照Allan方差使用手册就可以对应得到相应的误差模型

实际的Allan方差曲线往往只能表现出少数两三个主要误差类型，因为其它误差都被这几个主要误差给淹没了

4、一种更通用的样本方差分析方法

如下图所示，通用的样本方差分析方法与Allan方差不同之处是在分块、取平均之后，不是采取相邻块求差，而是截取连续M块求其标准方差，然后统计这些标准方差的样本均值，作为反映1~M倍块长度这个时间尺度区间的误差指标。这样就可以灵活地提取和评估我们所关心的任何时间尺度范围内的误差成份！

当M取2可得： 

 

 由于Allan方差取M=2这一最小值，因此它具有最高的时间尺度分辨率，对不微附件同时间尺度上的误差成份的刻画最细腻，因此被大家用得最多。

原稿见：https://blog.csdn.net/xhtchina/article/details/122417927