用四阶龙格-库塔方法求微分方程组

 最近一段时间再忙期末考试，小学期课程设计的东西，没怎么更新博客....

更新一个用四阶龙格库塔方法求解脉冲微分方程，题目来源是一篇论文《Impulsive control of projective synchronization in chaotic systems 》。

概述：

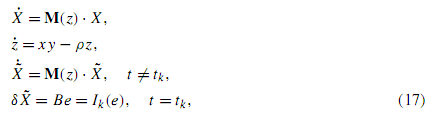
做法其实也很简单，就是原来求一个因变量的龙格库塔公式变成求五个因变量的龙格库塔公式，当然，变化求解的过程是有不一样的地方的，需要特别处理一下。

% 1
t = [];
x = [];
y = [];
z = [];
sigma = 10;
u = 28;
p = 8 / 3;
X = [];
x(1) = 1;
y(1) = 2;
z(1) = 3;
X(1,1) = 2;
X(2,1) = 1;
h = 0.01; 
a = 0;
b = 1;
t(1) = 0;
gain1 = -1.1;
gain2 = -1.1;
alpha = -3;
n = fix((b-a) / h);

for i = 2 : n+1
    t(i) = t(i-1) +  h;
    
    k11 = sigma * ( y(i-1)  - x(i-1) );
    k21 = (u - z(i-1)) * x(i-1) - y(i-1);
    k31 = x(i-1) * y(i-1) - p * z(i-1);
    k41 = sigma * (  X(2, i-1) - X(1,i-1) );
    k51 = X(1,i-1) * (u - z(i-1)) - X(2,i-1);
    
    k12 = sigma * ( y(i-1) + h / 2 * k21 - x(i-1) - h / 2 * k11  );
    k22 = (u - z(i-1) - h / 2 * k31) * (x(i-1) + h / 2 * k11 ) - y(i-1) - h / 2 * k21;
    k32 = (x(i-1) + h / 2 * k11)* (y(i-1)+ h / 2 * k21 )- p * (z(i-1) + h /2 * k31  );
    k42 = sigma * (  X(2, i-1) + h/2*k51- X(1, i-1) - h/2*k41);
    k52 = (X(1,i-1) + h/2*k41  )* (u - z(i-1) - h/2*k31) - X(2,i-1) - h/2*k51;
    
    k13 = sigma * ( y(i-1) + h/2 * k22 -  x(i-1)  - h / 2 * k12 );
    k23 = (u - z(i-1) - h/2*k32 ) * (x(i-1)+h/2*k12) - y(i-1) - h / 2 * k22;
    k33 = (x(i-1) +h/2*k12) *( y(i-1)+ h/2 * k22 )- p *(z(i-1) + h / 2 * k32);
    k43 = sigma * (  X(2, i-1) + h/2*k52- X(1, i-1) - h/2*k42);
    k53 = (X(1,i-1) + h/2*k42  )* (u - z(i-1) - h/2*k32) - X(2,i-1) - h/2*k52;
    
    k14 = sigma * ( y(i-1)+h*k23 - x(i-1) - h * k13 );
    k24 = (u - z(i-1) - h*k33) * (x(i-1)+h*k13) - y(i-1) - h * k23;
    k34 = (x(i-1) +h*k13 ) * (y(i-1) + h*k23) - p * (z(i-1) + h * k33 );
    k44 = sigma * (  X(2, i-1) + h/2*k53- X(1, i-1) - h/2*k43);
    k54 = (X(1,i-1) + h/2*k43  )* (u - z(i-1) - h/2*k33) - X(2,i-1) - h/2*k53;
    
    x(i) = x(i-1) +  h / 6 * (k11 + 2 * k12 + 2 * k13 + k14); 
    y(i) = y(i-1) + h / 6 * (k21 + 2 * k22 + 2 * k23 + k24);
    z(i) = z(i-1) + h / 6 * (k31 + 2 * k32 + 2 * k33 + k34);
    X(1, i) = X(1, i-1) + h /6 * (k41+ 2 * k42 + 2 * k42 + k44);
    X(2, i) = X(2, i-1) + h / 6 * (k51 + 2 * k52 + 2*k53 + k54);
    
    if mod(i, 15) == 0
        X(1, i) = X(1, i) + gain1 * (X(1,i) - alpha * x(i) );
        X(2, i) = X(2, i) + gain2 * (X(2,i) - alpha * y(i) );
    end

end
%plot(t, x, 'b-', t, y, 'k-', t, z, 'c-', t, X(1,:), 'r-', t, X(2,:), 'm-')
% plot(t, x, t, y)
%  plot(t, X(1,:), t, X(2, :) )
e1 = X(1,:) - alpha * x;
e2 = X(2,:) - alpha * y;
plot(t, e1, t, e2)
    
    

matlab代码跑出来的图