《算法导论》Ch.13_学习笔记

<红黑树>

红黑树是许多“平衡”搜索树中的一种，可以保证在最坏情况下基本动态集合操作的时间复杂度。

13.1红黑树的性质

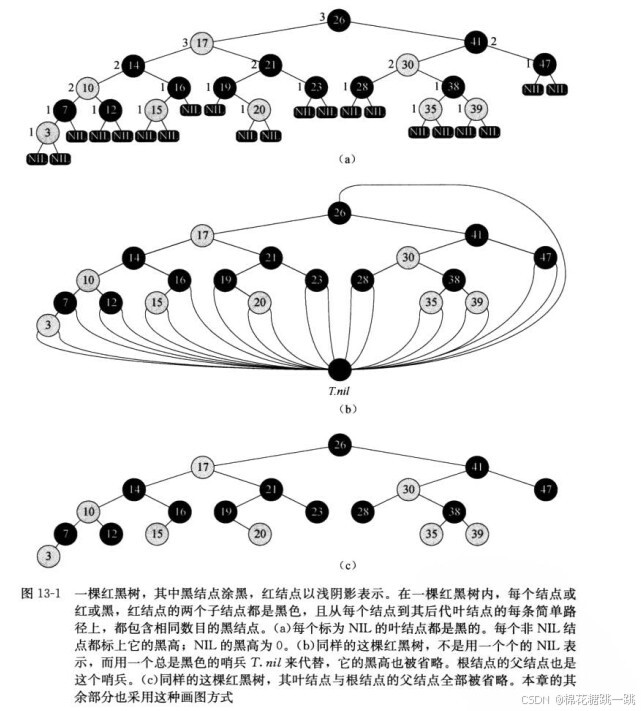
红黑树是一棵二叉搜索树，每个结点增加一个存储位表示结点的颜色（RED或BLACK）。

树中每个结点包含5个属性：color、key、left、right和p。如果一个结点没有子结点或父结点，则该结点相应指针属性的值为NIL。

一棵红黑树是满足下面红黑性质的二叉搜索树：

1. 每个结点或是红色的，或是黑色的。
2. 根结点是黑色的。
3. 每个叶结点(NIL)是黑色的。
4. 如果一个结点是红色的，则它的两个子结点都是黑色的。
5. 对每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点。

备注：

• 哨兵表示NIL。哨兵T.nil是一个与树中普通有相同属性的对象。
• T.nil的color属性为BLACK，其他属性可以设为任意值。
• T.nil使用一个哨兵来代表所有的NIL，所有的叶结点和根结点的父结点。

引理13.1 一棵有n个内部结点的红黑树的高度至多为。

13.2旋转

搜索树操作TREE-INSERT和TREE-DELETE在含n个关键字的红黑树上，运行时间为。

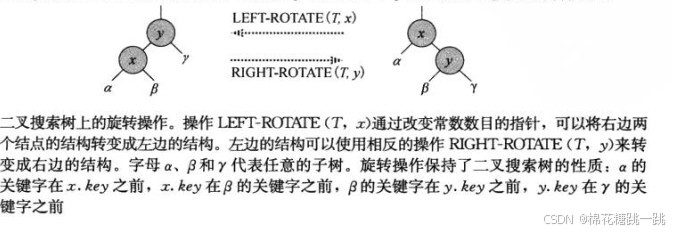
以左旋为例，左旋的伪代码如下。右旋的代码是对称的。

13.3插入

由于将z着为红色可能违反其中的一条红黑性质，所以在RB-INSERT的第17行中调用RB-INSERT-FIXUP(T,x)

13.4删除

删除结点z之后，RB-DELETE调用一个辅助过程RB-DELETE-FIXUP通过改变颜色和执行旋转来恢复红黑性质。