【论文笔记】【存储】SwapAdvisor: Pushing Deep Learning Beyond the GPU Memory Limit via Smart Swapping-CSDN博客

本文链接：https://blog.csdn.net/qq_43207982/article/details/134211925

[swapping between GPU and CPU memory] SwapAdvisor: Pushing Deep Learning Beyond the GPU Memory Limit via Smart Swapping. Chien-Chin Huang, Gu Jin, Jinyang Li. ASPLOS’20

论文地址：https://dl.acm.org/doi/pdf/10.1145/3373376.3378530

如何在有限的GPU内存中训练更大的模型，是一个亟待解决的问题。

为了解决这个问题，一个可行的解决方案是实现GPU和CPU内存之间的交换（swapping）。

但是，这个方案存在一个问题：如何决定哪些数据应该被存储在CPU内存中，哪些数据应该被存储在GPU内存中呢？这就需要一个优化算法来决定。

这就是SwapAdvisor的作用。

它可以根据给定的数据流图，进行运算调度（operator scheduling）、内存分配（memory allocation）和交换决策（swap decisions）的联合优化。SwapAdvisor使用了一个特定设计的遗传算法来遍历搜索空间。

本文中提的前人方法的不足：

现有的减小内存消耗的方法包括使用低精度浮点数或通过量化和稀疏化来压缩模型参数，但这些技术可能会影响模型的准确性，并需要大量的超参数调整。（然而量化是一个很不错的研究方向，可以用一些方法使得精度下降可以接受）
另一些方法是丢弃中间数据，并在需要时重新计算它们，但由于模型参数不能轻易地被重新计算，所以这些方法不能支持大型模型。（但是占比最高的内存占用应该是优化器状态，这是可以重计算的。反向传播的一些值也是可以计算的）

本文的研究方法：

一种有希望解决GPU内存限制问题的方法是在DNN计算过程中，在GPU和CPU内存之间交换张量数据。这种方法的吸引力在于：

1）CPU内存比GPU内存大得多且便宜得多；
2）现代GPU硬件可以有效地将通信和计算重叠；
3）GPU和CPU之间的通信带宽现在已经足够好，而且随着PCIe 5.0的到来和NVLink的广泛采用，它将显著增长。

这可能是文章的写作思路，实际上每个方向都是有人在研究的，也是有不少的成果的。

对于给定的DNN计算，SwapAdvisor在执行前精确地规划什么时候和要交换什么，以便最大化计算和通信的重叠。

本文的限制

它需要一个没有控制流原语的静态数据流图，并且只为单个GPU规划交换。

在计算机科学中，数据流图是一种描述程序执行过程的图形表示法。在数据流图中，节点表示运算，边表示数据的流动。

“没有控制流原语的静态数据流图”这个描述的意思是，该数据流图是在程序的执行开始之前就已经完全确定的，而且图中没有包含诸如if-else结构、循环或者跳转等控制流原语。这意味着程序的执行路径在程序开始前就已经完全被确定下来，而且程序执行时不会根据任何条件改变这个路径。

本文专注自动优化最佳的交换计划，以应对任意复杂的数据流图。
我们将讨论的重点放在单GPU交换上，但本文的设计可以用于使用数据并行在不同GPU上复制模型的多GPU训练设置。

本文对内存消耗的分析

DNN的内存消耗分为3类：

模型参数。在DNN训练中，参数在迭代结束时更新，并被下一次迭代使用。参数张量与DNN模型的"深度"（层数）和"宽度"（层的大小）成正比。对于大型模型，这些将占据内存使用的主要部分。
中间结果。这包括激活，梯度和误差张量，其中后两者仅在训练中存在，但在推理中不存在。
临时空间。某些运算符的实现（例如卷积）需要临时空间，最多达到一GB。临时空间是总内存使用的一小部分。

不知道为什么，他没有注意到优化器状态，在ZeRO的文章分析中，这个占比很大。

本文的设计思路

一个好的交换计划应尽可能地重叠通信和计算。重叠的机会来自交换出一个（暂时）未使用的张量，以便在后者被运算符执行所需之前，为交换入超出内存的张量腾出空间。我们希望通过数据流图的帮助，仔细规划何时以及交换什么，以最大化这样的重叠。

特别是，本文认为影响交换计划的有两个关键因素：

内存分配。DNN计算使用了各种大小的张量，从几KB到数百MB。为了提高速度并减少内部碎片，像MXNet这样的框架使用了内存池，预先分配了各种大小类中的固定大小的张量对象。因此，交换不仅发生在GPU内存满时，还发生在特定大小类中没有空闲对象时。因此，如何配置内存池以进行分配，可能会严重影响交换性能。
运算符调度。现代DNN往往具有复杂的数据流图，因为层不再形成链，而是包含分支、连接和展开的循环。因此，有许多不同的运算符执行计划。执行顺序可以深刻影响内存使用，从而影响交换的性能。

由于内存分配和运算符调度对交换性能有着关键的影响，本文根据给定的数据流图、相应的内存分配方案和运算符调度，推导出一个交换计划（即何时、交换哪些张量进出）。具体来说，交换计划通过交换出未来最长时间内不需要的张量，以及尽早预取先前交换出的张量，优化了计算和通信的重叠。

我们搜索可能的内存分配和运算符调度空间，以找到交换性能最佳的组合。我们没有使用人工启发式方法来约束和指导搜索，而是采用了遗传算法（GA）[5, 8, 18]来搜索内存分配和运算符调度的好组合。

这里的[5, 8, 18]就不展开了，需要学习的可以自行学习遗传算法

我们选择遗传算法而不是其他搜索启发式（例如模拟退火），是因为它快：遗传算法可以并行化，并在多核CPU上高效计算。

为了有效地探索广阔的搜索空间，我们必须能够快速评估任何内存分配/调度组合下的交换计划的整体性能（即端到端执行时间）。我们发现在真实的框架上执行实际操作太慢了。因此，我们通过在数据流引擎模拟器下运行交换计划来估计性能。模拟器使用每个运算符的测量计算时间以及GPU-CPU通信带宽，因此它可以估计给定调度、内存分配和交换计划下的数据流图的执行时间。我们模拟器在CPU核心上的运行时间比实际执行快几个数量级，将对一个模型的搜索时间减少到不到一个小时。模拟器使SwapAdvisor的遗传算法能够直接优化端到端执行时间。

本文是在数据流引擎模拟器上去找最优解的，而不是真实系统上运行的。通过使用模拟器，SwapAdvisor的遗传算法能够直接优化端到端的执行时间，从而在广阔的搜索空间中找到最优的内存分配和调度方案。

深入本文的设计

在这里插入图片描述

它与现有的DNN框架（在我们的实现中是MXNet）集成。给定一个数据流图，SwapAdvisor根据图选择任何合法的调度和内存分配作为初始值，并将它们传递给交换规划器以确定何时、将哪些张量交换进出。交换规划器的结果是一个扩展的数据流图，其中包括额外的交换进和交换出运算符以及额外的控制流边。额外的边是为了确保最终执行顺序符合给定的调度和规划器的交换时机。

对于优化，扩展图被传递给SwapAdvisor的数据流模拟器来估计整体执行时间。SwapAdvisor的基于GA的搜索衡量许多内存分配/调度组合的性能，并为交换规划器提出新的分配/调度候选方案。一旦交换计划已经充分优化，最终的扩展数据流图就会被提供给框架进行实际执行。、

除了数据流图，交换规划器还接受运算符调度和内存分配作为输入。也就是上图的Swap Planner。

操作符调度

给定一个无环数据流图G，运算符调度是G中节点的任何拓扑排序。当使用单一GPU时，框架可以按照调度向GPU发出运算符，以保持GPU忙碌。实际上，像MXNet这样的框架通常进行拓扑排序来调度运算符。

设想你是一家快餐店的经理，你的店里有不同的工作岗位，比如接单、煎汉堡、制作薯条、倒饮料等。每个岗位都对应一个操作，而每个操作都需要一定的时间完成。此外，这些操作之间还存在一定的依赖关系，比如你不能在汉堡还没煎好之前就开始包装。

你要做的就是找出一个顺序，让所有的操作都能按照这个顺序进行，而且不违反任何依赖关系。比如，你可能会先让员工接单，然后煎汉堡，接着制作薯条，最后倒饮料。

运算符调度就是类似的过程。在给定的无环数据流图中，每个节点代表一个操作，每个操作都需要一定的时间完成。此外，这些节点之间还存在一定的依赖关系，比如你不能在一个节点的操作还没完成之前就开始执行依赖于它的节点的操作。

运算符调度就是找出一个顺序，让所有的节点都能按照这个顺序进行，而且不违反任何依赖关系。这就像快餐店经理找出一个顺序，让所有的操作都能按照这个顺序进行，而且不违反任何依赖关系一样。

这种调度方法能确保GPU始终保持繁忙状态，从而提高了GPU的使用效率。

NVIDIA的最近的GPU支持多个“流”。SwapAdvisor使用3个流：一个用于执行GPU运算，一个用于将张量交换出到CPU，一个用于从CPU交换进张量。由于GPU-CPU通信是双工的，所以当以这种方式使用时，所有三个流可以同时进行。相比之下，如果一个人要使用多个流进行计算，那么如果没有足够的GPU计算资源进行并行执行，这些流不能同时执行。我们观察到，在所有我们测试过的DNN模型中，使用多于一个流进行计算并没有性能优势。

内存分配

我们需要为给定的数据流图配置内存池并指定内存分配。内存池由多个不同的大小类别组成，每个类别都被分配了一定数量的固定大小张量对象。给定一个包含每个运算符所需的所有输入/输出张量大小的数据流图G，可以通过指定两件事来定义一个内存分配方案：

1）从G中的每个张量大小到内存池支持的某个大小类别的映射。
2）支持的大小类别集合以及分配给每个类别的张量对象数量。

作为一个例子，图1(b)©中的粗粒度分配方案只有一个大小类别（2MB）与5个对象，并将每个1MB或2MB的张量映射到2MB大小类别。图1(d)(e)中的细粒度方案有两个大小类别（1MB和2MB），分别有8个和1个对象，并将每个1MB的张量映射到1MB大小类别，每个2MB的张量映射到2MB大小类别。

这里就是说粒度的问题，前面的是只有2MB的分区，所以1MB和2MB都是映射到2MB。后者两个大小类别都有，就1MB -> 1MB，2MB -> 2MB。

交换规划

交换规划器被赋予数据流图以及有效的运算符调度和内存分配方案。它的任务是在给定的调度/分配组合下找到性能最好的交换方案。特别是，交换规划器决定：

1）在内存压力下要交换出哪些内存驻留张量，
2）何时执行交换进或交换出。

在高层次上，交换规划器使用Belady的策略来选择在未来最长时间内不会被需要的张量进行交换出。由于规划器拥有调度信息，所以它可以“预见未来”。Belady的策略对于缓存替换是最优的，并且在我们的情境中也非常有效，因为它给规划器足够的时间在下次使用前将张量交换回来。

具体来说，规划器按照调度中的顺序扫描每个运算符，并跟踪由于执行运算符序列而在内存中驻留的输入/输出张量对象的集合。当添加大小为s的张量时遇到内存压力（即s大小类别中没有可用的对象），规划器选择从与s同一大小类别中的张量进行交换出。如果有多个候选对象，规划器会选择将在未来最远的时候使用的那一个。

Belady的策略，也被称为Belady的最佳性原则或最长未来使用距离(LFUD)策略，是一种用于缓存替换的策略。这个策略的基本思想是，当需要为新的元素腾出缓存空间时，应该选择在未来最长时间内不会被访问的元素进行替换。换句话说，这个策略会优先替换那些未来访问最不频繁的元素。

这里需要注意一个点：

首先，让我们设想一下我们有两个运算符，opi和opj，以及两个张量，Ti和Tj。Ti是运算符opi的输出张量，也就是说，它是opi运算的结果。Tj是opj的输入张量，也就是说，它需要被opj使用。
现在，假设我们的内存空间有限，我们需要为新的张量Tj腾出空间。根据Belady的策略，我们选择在未来最长时间内不会被访问的张量进行替换，这个张量就是Ti。但是，问题在于，我们不能立即交换出Ti，因为它仍被opi使用。我们只能等到opi完成之后，才能交换出Ti。
这就引出了一个问题：如果opi和opj的执行时间非常接近，那么在opj需要使用Tj之前，可能没有足够的时间将Ti交换出，然后把Tj交换进来。因为要等opi完成，Ti才能被交换出，这个时间可能比opj开始执行的时间还晚。
为了解决这个问题，规划器在选择要交换出的张量时，会选择那些至少在一段阈值时间前最近被使用过的张量。这个“阈值时间”实际上是一个缓冲区，它保证了有足够的时间将Tj交换进来，而不会影响opj的执行。

为什么选择至少在一段“阈值时间”前最近被使用过的张量呢？这是因为这些张量的使用时间已经过去了一段时间，而且在近期内都不会再被访问。这意味着我们可以安全地将这些张量交换出去，而不需要担心这会影响到它们的使用。同时，因为这些张量的使用时间已经过去了一段时间，所以我们有足够的时间将新的张量交换进来。
总的来说，这个“阈值时间”是一个平衡点，它既可以保证我们有足够的时间将新的张量交换进来，又可以保证我们不会过早地将还需要使用的张量交换出去。

DNN训练是迭代的，但是交换规划器只给出了单次迭代的数据流图。在每次迭代结束时，除参数张量外的所有张量都可以被丢弃。然而，为了确保同一交换计划可以在多次迭代中使用，我们必须确保在迭代结束时GPU内存中的参数张量集合与开始时相同。为了实现这一点，我们进行双遍扫描，即扫描调度以进行两次交换规划。在第一次扫描中，我们假设没有参数张量在GPU内存中，并且在第一次使用前必须交换进来。在第一次扫描结束时，一部分参数张量在内存中变为驻留状态，我们称之为初始驻留参数。然后我们进行第二次扫描，假设初始驻留参数在调度开始时已经在内存中。在第二次扫描中，如果出现了在第一次扫描中没有发生的额外内存压力，我们会从初始驻留集合中移除一个参数张量以解决这个问题。最终的交换计划的初始GPU驻留参数不包括在第二次扫描中被移除的那些。

让我们通过一个故事来理解这个概念。

想象一下你正在管理一个图书馆。你的目标是确保读者在需要的时候能找到他们想要的书。这个图书馆的空间有限，不能容纳所有的书，所以你需要定期将一些书放入仓库，并从仓库中取出一些书放到图书馆中。这就像是交换规划器在管理GPU内存，决定哪些张量（书）应该在内存（图书馆）中，哪些应该被交换出去（放入仓库）。

现在，你的图书馆正在举办一个研究小组活动，每天都会有一次会议。每次会议的开始和结束，都有一些必须的书籍需要在图书馆中。这就像DNN训练的每次迭代，有一些参数张量（书）必须在迭代开始和结束时在GPU内存中。

为了管理这个活动，你决定制定一个调度计划。你首先进行一次扫描，假设在活动开始时，没有必要的书在图书馆中，你需要将它们从仓库中取出来。这就是第一次扫描。在这次扫描结束时，你会发现有一部分必要的书仍然在图书馆中，我们称之为初始驻留的书。

然后你进行第二次扫描，这次你假设所有初始驻留的书在活动开始时已经在图书馆中。如果在这次扫描中，你发现有一些书需要更多的空间，你就会从初始驻留的书中移除一本，以腾出空间。这就是第二次扫描。

最后，你的调度计划会确保，在每次会议开始时，所有必要的书都在图书馆中，而不包括在第二次扫描中被移除的那些书。

通过这个故事，你可以理解为什么需要进行双遍扫描，并且如何通过两次扫描来确保在每次迭代开始时，所有需要的参数张量都在GPU内存中。

究其原因就是，每次迭代完成之后很多内存都是可以free掉的，但是又不是全部可以free掉，有些下个迭代还要用。

内存交换的时机

这里的内容讲的是交换策略，也就是在什么时候应该将张量从GPU内存中交换出去，以及在什么时候应该将张量交换进GPU内存。交换策略的目标是在不阻碍计划中的运算符执行的前提下，尽可能早地完成交换操作，以最大化计算和通信的重叠。

让我们以一个3节点的数据流图和一个运算符调度（op1，op2，op3）为例（见下图）。为了简便起见，我们假设所有的张量都是1单位大小，而GPU内存总大小为4单位。为了执行op1，我们必须将参数张量W1交换进来，因此规划器添加了一个新的数据流节点，用于在专用于交换进来的GPU流上运行W1。同样的，我们也为W2添加了一个交换进来的节点。我们注意到，有足够的内存来容纳op1和op2的输入/输出张量。然而，为了运行op3，我们需要为W3和A3留出空间。规划器选择将W1交换出去，以为W3腾出空间（称为W1 → W3），并选择将W2交换出去，以为A3腾出空间（称为W2 → A3）。

让我们首先考虑W1 → W3的情况。规划器添加了两个数据流节点：W1(交换出)和W3(交换进)。添加了一个从W3(交换进)到op3的控制流边，以确保在W3进入GPU内存后才开始运算符的执行。添加了一个从W1(交换出)到W3(交换进)的边，以确保在相应的交换出完成后内存变为可用，才开始交换进。此外，还包含了一个从op1到W1(交换出)的边，因为在op1完成使用W1之前，W1不能从内存中移除。

W2 → A3的情况类似，只是规划器不需要为A3添加一个交换进来的节点，因为A3是由运算符创建的。最后得到的增强数据流图可以传递给框架的数据流引擎进行执行。

这段内容的关键是理解交换的时机和条件。在保证安全的前提下，我们希望尽可能早地完成交换，以优化计算和通信的效率。同时，我们还需要确保在运算符使用张量的过程中，不会因为交换操作而导致张量不可用。

在这里插入图片描述

通过遗传算法进行优化的过程

遗传算法（GA）的目标是通过自然启发的机制（如交叉、突变和选择）来进化和改进一个整体的个体群体。

在SwapAdvisor中，一个个体的染色体由两部分组成：一个运算符调度和一个内存分配。第一代个体是随机创建的，群体的大小由一个超参数Np决定。

为了创建新一代的个体，我们对当前一代的染色体进行交叉和突变。交叉会接收一对父母染色体，并通过组合父母的特征来产生新的个体，这样子代可以（概率性地）从父母那里继承“好”的特性。在SwapAdvisor中，每次交叉会生成两个新的调度和两个内存分配，从而得到4个子代。然后我们对子代进行突变，这对于遗传算法来说至关重要，因为它可以帮助遗传算法逃离局部最小值并避免过早的收敛。经过突变的子代被交给交换规划器，生成带有交换节点的增强数据流图。我们使用一个定制的数据流模拟器来执行增强图并获得执行时间，这个时间用来衡量一个个体的质量。最后，遗传算法从当前的群体中选择Np个个体，让他们存活到下一代。

这个过程模拟了自然界的进化过程，通过不断地交叉、突变和选择，使得群体中的个体不断改进和进化，从而寻找到最优的解决方案。

遗传算法中如何选择存活下来的个体

如果我们只选择最优秀的个体存活下来，群体可能会丧失多样性并过早收敛。SwapAdvisor的选择策略考虑了个体的质量来决定其存活的概率。

假设一个个体的执行时间为t，我们定义其标准化执行时间为tnorm = (TBest −t )/TBest，其中TBest是迄今为止所有个体中最好的时间。一个个体的存活概率由softmax函数决定。如下：
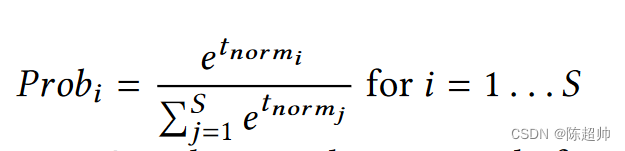
在这里插入图片描述
我们使用基于softmax的选择方法，因为我们的实验显示，与流行的锦标赛选择方法相比，它能得到更稳定的结果。这种方法保证了优秀个体的存活概率更高，但同时也给了其他非最优个体一定的存活机会，以保持群体的多样性并防止过早收敛。

创建新的调度的方法

首先，我们先看一下调度编码的过程。调度是数据流图的拓扑排序，换句话说就是一个按照依赖关系进行排序的节点列表。例如，对于一个包含5个节点的数据流图，一种可能的调度是[2, 3, 1, 4, 5]，这表示先执行节点2，然后执行节点3，依此类推。

看图：
在这里插入图片描述

交叉操作：

这部分内容描述了遗传算法中的交叉过程，主要是基于两个父调度（例如，SCH1 = [2, 3, 1, 4, 5] 和 SCH2 = [3, 1, 2, 4, 5]）生成两个子调度。首先，随机选择一个交叉点（在这个例子中，交叉点CR = 3）。为了创建第一个子调度SCHC1，交叉操作将SCH2的一部分（[2, 3, 4]）作为SCHC1的第一部分。然后，将不在这部分的节点（在这个例子中，节点1和节点5不在SCHC1中）按照它们在SCH1中的顺序填充到SCHC1的其余位置，得到SCHC1 = [2, 3, 4, 1, 5]。使用类似的方法，你也可以生成另一个子调度SCHC2。这个算法保证了SCHC1和SCHC2都是图G的拓扑排序。

最后，我们来看突变的过程。突变的目的是在保证拓扑排序的前提下，随机改变调度中的某些节点的位置。例如，我们可以把SCHC1中的节点2和节点4交换位置，得到新的调度**[3, 1, 4, 2, 5]**。SwapAdvisor的突变算法更加复杂一些，它不是简单地随机交换两个节点的位置，而是模仿了一个数据流调度器的行为，维护了一个准备运行的节点集合，根据一定的概率规则，有可能随机选择一个节点进行突变，也有可能选择原始调度中最早执行的节点。

这些都是遗传算法中的基本操作，通过不断的交叉和突变，然后选择出最优的个体，可以找到最优的解决方案。

让我们用一个故事来帮助你理解这个过程（数据可能不同，但是思想差不多，理解思想很重要）。

想象一下你是一位乐队的指挥，你的乐队有五位音乐家，他们分别负责不同的乐器。我们分别用数字1-5来代表他们。现在你要为一首曲子安排演奏的顺序，这就像是调度编码的过程。

你首先制定了一个演奏计划，比如[2, 3, 1, 4, 5]，这表示首先由2号音乐家开始演奏，然后是3号音乐家，依此类推。

然后，你的助手也给你提供了一个他认为的优秀的演奏顺序，比如[3, 1, 2, 4, 5]。你们决定尝试结合两个计划，创造出新的演奏顺序。这就像是交叉的过程。

你们随机选择一个切换点，比如3（代表在第三个音乐家开始切换）。然后，你从你助手的计划中取出前三个音乐家的顺序（[3, 1, 2]），并将其作为新计划的开始。然后，你将剩下的音乐家（4和5）按照在你原来计划中的顺序添加到新计划的后面。所以你得到了一个新的演奏顺序：[3, 1, 2, 4, 5]。同样的方法，你们也可以生成另一个新的演奏顺序。

然后，你决定尝试一些新的想法，看看是否能增强乐曲的效果。这就像突变的过程。

你可能决定交换两位音乐家的演奏顺序，例如，你可能把2号音乐家和4号音乐家的位置互换，从而得到一个新的演奏顺序：[3, 1, 4, 2, 5]。这个过程和论文中描述的SwapAdvisor的突变算法类似，不过SwapAdvisor的突变更复杂一些，它模仿了一种数据流调度器的行为，有可能随机选择一个节点进行突变，也有可能选择原始调度中最早执行的节点。

通过这样的方式，你可能会找到一种最优的演奏顺序，使得整首曲子的效果达到最佳。这就像是论文中通过遗传算法找到最优调度的过程。

如何创建新的内存分配编码

内存分配控制如何将每个大小映射到一个大小类，并决定为每个大小类分配多少对象。虽然使用哈希映射来将张量大小映射到大小类看起来很自然，但这样做会丧失不同张量大小之间的相对大小信息，从而使得交叉操作更加困难。作者使用了两个列表，CLS 和 CNT，来表示张量大小-类别映射。

这里，TS 是观察到的数据流图中唯一张量大小的排序列表。CLS 是一个和 TS 长度相同的列表，列表中的第 i 个项 CLS[i] 是一个正整数，代表大小为 TS[i] 的张量的大小类。因此，大小类的数量是 Max(CLS)。CNT 是一个列表，表示为每个大小类分配的张量对象的数量。因此，CNT 的长度是 Max(CLS)。

接下来，作者讨论了如何进行交叉操作。首先，随机选择一个交叉点，将父列表 CLS1 和 CLS2 分为两部分。第一个子大小类映射 CLSC1 是通过连接 CLS2[1…CR] 和 CLS1[CR+1…N] 来创建的。第二个子大小类映射 CLSC2 是通过连接 CLS1[1…CR] 和 CLS2[CR+1…N] 来创建的。需要注意的是，如果新的大小类映射不是单调递增的，我们需要修复它，使得它成为有效的大小类映射。修复的方法是以最小的量增加问题列表中的元素，使得结果序列变得有效。

对于 CNT，我们不能直接使用相同的交叉方案，因为它的长度取决于相应的 CLS 的内容。因此，我们将 CNT 扩展到一个长度与 CLS（和 TS）相同的 CNTEXT。CNT 捕获了为每个大小类分配了多少张量对象，而 CNTEXT 表示每个张量大小可以使用多少张量对象。我们使用相同的技术来交叉扩展的 CNT。然后，我们对同一个大小类中的所有元素取平均值，得到该大小类的计数。新的 CNT 也可能需要修复。我们通过将每个元素按照与元素对应的大小类的倒数比例减少来修复 CNT。

总的来说，这一部分介绍了如何通过交叉和修复操作来创建新的内存分配编码，这对于遗传算法的性能和有效性有着重要的影响。

这个比较抽象，我们通过一个故事来理解。

假设你是一个城市规划师，你现在正在设计一个城市的建筑物布局。这个城市有各种各样的建筑，包括住宅、商业大厦、学校等，每种建筑都有它们自己的大小需求。比如，住宅可能只需要一小块地，而商业大厦可能需要更大的土地。这就好比论文中的张量，它们有各自的大小需求。

你的任务是将这些建筑物分配到不同的地块上，这些地块是预先规划好的，每个地块都有一个大小类，代表着它能容纳的建筑大小。这就好比论文中的大小类。

你的目标是尽可能有效地利用所有的地块，这就好比论文中的内存分配。你需要一个地块分配方案，告诉你应该在哪个地块上建造哪种类型的建筑，这就好比论文中的CLS 列表。

然后，你还需要知道每个地块上应该建造多少个建筑，这就好比论文中的 CNT 列表。

现在假设你有两个规划方案，你需要决定哪个更好。你在比较这两个方案的时候，可能会发现，如果你将这两个方案进行某种组合，可能会得到一个更好的结果。这就好比论文中的交叉操作。

但是，你不能随便组合，因为如果你把一个大楼放在一个只能建住宅的地块上，那就不对了。所以，你需要修复这个组合方案，确保每个地块上的建筑物都符合地块的大小限制。这就好比论文中的修复操作。

通过这样的方式，你可能会找到一个最优的城市规划方案，使得所有的地块都被最大限度地利用。这就好比论文中的最优内存分配方案。

这里的变异操作

主要涉及到CLS（Class size list，大小类列表）和CNT（Count list，数量列表）的变异。让我们用通俗的语言解释一下这些操作。

在变异过程中，CLS和CNT中的多个元素都有可能发生变化，变异的概率为P。每个元素可以增加1或减少1。

变异CLS的第i个元素时，如果CLS[i]等于CLS[i-1]，那么增加CLS[i] 1个单位，因为减少它会破坏单调递增的特性。如果CLS[i]等于CLS[i-1] + 1，那么减少CLS[i] 1个单位。需要注意的是，为了保持单调递增的特性，第i个元素之后的所有元素也需要相应地增加或减少。

对于CNT中的元素的变异，我们使用高斯分布进行随机变异，原始值作为高斯分布的均值。由于高斯分布的特性，大多数时候变异后的值会接近原始值，但有小概率产生较大的变化。

变异后的CNT和CLS可能会超过内存限制，我们使用与交叉操作相同的方法进行修复。

我们可以用一个简单的故事来帮助理解：
你正在拼图，你有一个分类列表（CLS），记录了不同大小的拼图块有多少个，还有一个计数列表（CNT），记录了每种大小的拼图块需要用多少次。现在你想改变一下拼图的样式，你可以决定增加或减少某个大小的拼图块的数量（这就是变异CLS），或者改变每种大小的拼图块使用的次数（这就是变异CNT）。但你要注意，你的桌子大小有限，所以所有的拼图块总体积不能超过桌子的大小。如果变异后的拼图块超过了桌子的大小，你就需要按照一定的规则来调整拼图块，使得它们再次适应桌子的大小。

在这里插入图片描述
这个图非常复杂。

首先看图a，上面是1,1,1,1，下面是1,2,2,2。用上述那个图的变异方法得到 CLS(c1)是1,2,1,1。但是这个结果是不合理的，因为他不是单调递增的，这不符合内存规则，所以修复他是1,2,2,2。

图a的下面的1，1, 2，2就没啥问题了，就不用修复

图b的CNT 捕获为每个 sizeclass 分配了多少个张量对象，而CNTEXT 指示每个张量大小可以使用多少个张量对象。
这里很抽象，论文中提到是说CNT1是4，可以扩展为CNTEXT1（4,4,4,4）.CNT2是（8,1），可以扩展为CNTEXT2（8,1,1,1）。然后才用这个4,4,4,4和8,1,1,1做交叉，得到图上的CNTEXTC1和CNTEXTC2，那个所谓的8,1,4,4和4,4,1,1。
不知道为啥作者没有把这个中间过程画出来。
这个平均过程就更抽象了，关注8,1,4,4这个数。由于是从8,1,1,1交叉过来的一部分，其中这个8是1MB的，1是4MB的。按照递增的原则，后面跟着的4,4也应该是4MB的。所以按照大小做平均就会得到8,3。然而这个是超过了内存容量的，所以要修复，按照比例修复，一人减少一半，变成了4,2。

写在最后，我感觉这篇文章还是比较抽象的，他没有那么的make sense。
首先他要做的是一个交换的最佳策略，他是要考虑三个方面的事情