算法评估指标简介
对于聚类,分类,回归三大算法类,有不同的算法评估指标,不同的评估指标.
- 分类算法常用评估指标:准确率,查准率,查全率,F1-score,PR曲线,ROC曲线和AUC指标,ROC曲线下的面积就是AUC指标.
- 聚类算法常用评估指标:轮廓系数 SSE(误差平方和)
- 回归算法的评估指标:R方范围[-inf,1] (真实值与预测 ),MSE,MAE,RMSE
分类算法评估指标
混淆矩阵
在介绍评估指标之前,先来认识一下混淆矩阵,在分类任务下,预测结果和真实结果之间存在四种不同组合,这四种不同结果构成了混淆矩阵

看着这个表确实挺混淆的,不愧是混淆矩阵。
接下来我来解释一下这个混淆矩阵,它分为预测结果和真实结果
我们知道预测结果不一定全是对的,需要和真实结果来作比较,比如在真实结果中有5个正例,95个反例;
- 真实结果:0 0 0 0 0 0 0 0…0 0 0 1 1 1 1 1
预测结果:0 0 0 0 0 0 0 0…1 1 1 1 1 1 0 0
1为要预测的值 - 那么在预测结果预测为正例§中的3个预测正确的数据就是真正例TP
- 在预测结果中预测为正例中的3个预测错误的数据就是伪正例FP
- 在预测结果中预测为反例(N)中的2个预测错误的数据就是伪反例FN
- 在预测结果中预测为反例中的92个预测正确的数据就是真反例TN
精准率(precision)
精准率也叫查准率,即预测结果中为1的6个中有几个是预测正确的,在混淆矩阵中精准率为TP/( TP+FP )
召回率(recall)
召回率也叫查全率,即真实结果中为1的5个中预测出了几个正确的,在混淆矩阵中召回率为TP/( TP+FN )
导包的使用
# 代码中用于计算精准率和召回率的导包为
from sklearn.metrics import confusion_matrix
# metrics意为度量,参数为真实结果和预测结果
# 返回值为四个tn、fp、fn、tp,
# 精准率和召回率需要自己计算
from sklearn.metrics import precision_score
# 只能计算精准率,参数为真实结果和预测结果,average默认只关注类1
from sklearn.metrics import recall_score
# 只能计算召回率,参数为真实结果和预测结果,average=None为类1和类0的列表
f1-score
计算公式f1 = 2*PR/(P+R)
原理是计算了各类精准率的均值和召回率的均值,在不同算法下精准率和召回率不太好选择时使用f1-score
f1-score导包的使用
from sklearn.metrics import f1_score
# 参数和上面的相同
分类报告
from sklearn.metrics import classification_report
# 参数和上面相同

分类报告的返回值:返回各类的精准率,召回率,f1-score,和数据数量,accuracy为准确率,macro avg为均值,weighted avg为加权平均【(420.93+720.95)/114】
但是从中拿去数据还是比较麻烦的,大多数做观察使用
PR曲线
用于比较多种不同的算法预测结果的好坏程度,精准率P做y轴,召回率R做x轴,给出不同的正类范围绘出不同的P和R绘制曲线,根据面积的大小来判断算法的好坏
from sklearn.metrics import plot_precision_recall_curve
# 参数是算法类型,测试集特征,测试集标签

在PR曲线中,表示的精准率和召回率,在分类任务中,往往是随着精准率的逐渐增大,召回率是逐渐减小的,所以需要在PR曲线中找到他们的近似的平衡点,才能代表相对较好的结果
ROC曲线和AUC指标
ROC曲线又叫受试者工作特征,和PR曲线比较类似,但是它是以类1的召回率(真正例率)TPR=TP/( TP+FN )作为y轴,以1 - 类0的召回率(假正例率)FPR=FP/(TN+FP)=1 - [ TN/(TN+FP) ]。
from sklearn.metrics import plot_roc_curve
# 参数是算法类型,测试集特征,测试集标签
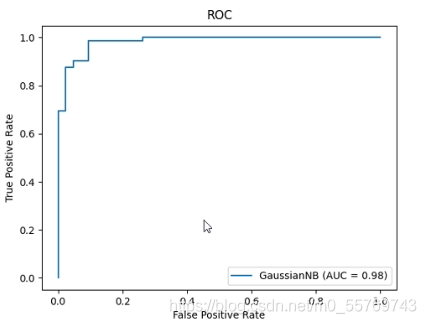
ROC曲线则是假正例率趋于0,真正例率趋于1的时候是最好的点,也就是说类1的召回率和类0的召回率都趋近于1时效果最好。
AUC指标为ROC曲线下的面积
聚类算法评估指标
手肘法获取K-means的最优K值
计算不同k值的SSE,绘制图像,选择图像拐点的k值相对是比较好的,由于图像画出来类似于手肘,所以叫手肘法,选取手肘拐点即可。手肘法选取的就是相对较好的点,也就相当于一个折中效果,使预测结果不会太差,防止过拟合现象的发生

获取最优轮廓系数
如果想要最优的点,还是要选取最高的点。
设置不同的k值进行测试计算轮廓系数,就能得到最优的k值对应的最优的轮廓系数,也可以绘图进行观察,选取最高。但是为了防止过拟合的现象,也可以通过手肘进行选取最优k值
from sklearn.cluster import KMeans
from sklearn.preprocessing import MaxAbsScaler # 小数定标标准化
from sklearn.preprocessing import MinMaxScaler # 离差标准化
from sklearn.preprocessing import StandardScaler # 标准差标准化
# 评估指标-----轮廓系数
from sklearn.metrics import silhouetee_score
# 由于是聚类算法,数据可能存在量纲,需要标准化,在使用算法之前
# 实例化
sca = MaxAbsScaler()
sca = MinMaxScaler()
sca = StandardScaler()
# 拟合
sca.fit( 训练集特征 )
# 处理数据
X_train = sca.transform( 训练集特征 )
# 实例化
km = KMeans()
# 参数:
# n_clusters=3,表示k=3,也就是随机三个聚类中心,最小值是2
# init,聚类中心初始化方法,默认k-means++
# max_iter,最大迭代次数,默认300,如果后期无法收敛可以尝试增加迭代次数
# random_state=1,随机种子,默认是None
# 拟合
km.fit( 训练集特征 )
# 查看聚类中心
print('聚类中心:', km.cluster_centers_)
# 查看预测结果
# 可以直接传入训练集,也可以传入自定义二维数组
y_pred = km.predict( 训练集特征 )
print('整个数据的类别:', y_pred)
# 查看SSE---误差平方和
# 默认是取反操作,大多数情况得出来的是负值【-inf, 0】
# 绝对值越小越好
score = km.score(X_train, y_pred)
print('SSE', score)
# 评估指标----轮廓系数(-1, 1),越大越好
print('轮廓系数:', silhouetee_score(X_train, y_pred))
回归算法评估指标
回归算法评估指标—R2
R2也就是score,也就是我们在分类算法中经常说的准确率,在回归算法中不能称为准确率,成为R2.

其最好的结果就是u=0,即真实值等于预测值,此时R2等于1
比较差的结果就是u=v,预测结果为均值,也就是直接拿了真实结果取了个均值作为预测值,此时R2=均值
最差的结果就是u>>v,此时真实结果远大于预测结果,还不如直接拿均值作为预测结果,R2的范围为-inf
回归算法评估指标—MSE
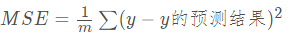
MSE观察的是真实结果和预测结果误差的平方的均值,也叫做均方误差.这种方式会将误差扩大一倍
回归算法评估指标—MAE
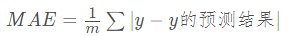
MAE是平均绝对误差,解决了MSE误差扩大的问题
回归算法评估指标—RMSE

RMSE便是在MSE的结果上开平方了
回归算法评估指标基于sklearn实现
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso # 套索回归
from sklearn.linear_model import Ridge # 岭回归
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error # mse
from sklearn.metrics import mean_absolute_error # mae
# RMSE 需要自己实现 np.sqrt(mse)
import numpy as np
out = load_boston()
X, y = out.data, out.target
X_train, X_test, y_train, y_test = train_test_split(X,
y,
test_size=0.2,
random_state=1,
)
# alpha 控制正则化的力度
# alpha=0 就 等于普通的线性回归
# alpha=1 就部分系数变为0
# alg = Lasso(alpha=100)
alg = Ridge(alpha=0)
alg.fit(X_train, y_train)
print("回归系数", alg.coef_)
print("回归截距", alg.intercept_)
print("R2", alg.score(X_test, y_test))
y_pred = alg.predict(X_test)
print("MSE", mean_squared_error(y_test, y_pred))
print("MAE", mean_absolute_error(y_test, y_pred))
print("RMSE", np.sqrt(mean_squared_error(y_test, y_pred)))























 924
924











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










