多商品流问题
1 引言
多商品流问题(MCFP)处理的是网络中商品流从源头到目的地的分配问题。MCFPs和包括交通和电信在内的几个领域都高度相关。几十年来,许多研究人员对MCFPs进行了研究,提出了多种解决方案,如列生成、拉格朗日松弛、分支定界和Dantzig-Wolfe分解。
2 多商品流问题
MCFP似乎是几个单一商品流动问题的组合。然而,由于商品之间的相互作用,MCFP的复杂性远远高于单独解决单个商品流动问题。为了解决MCFPs问题,必须考虑两个必要的约束条件。第一个是运输需求,这意味着所有的商品都需要运输到目的地。二是边的容量约束。这意味着在每条边上的流量不能超过其容量。第一个约束本质上是一系列单一商品流动问题的总和。然而,第二个约束需要把所有的商品都考虑到一起,导致了商品间的相互影响。是有向网络图。其中,
和
分别是大小为
和
的节点和边的集合。对于每条边
,都有成本
和容量容量
。t种商品需要从出发地节点运输到目的地节点。用
和
表示商品k的起点和目的节点。此外,
是商品k的运输需求。在此问题中,必须找到一个成本最小的最优流量分配,以满足运输需求和容量约束。因此,MCFP可以表述为:
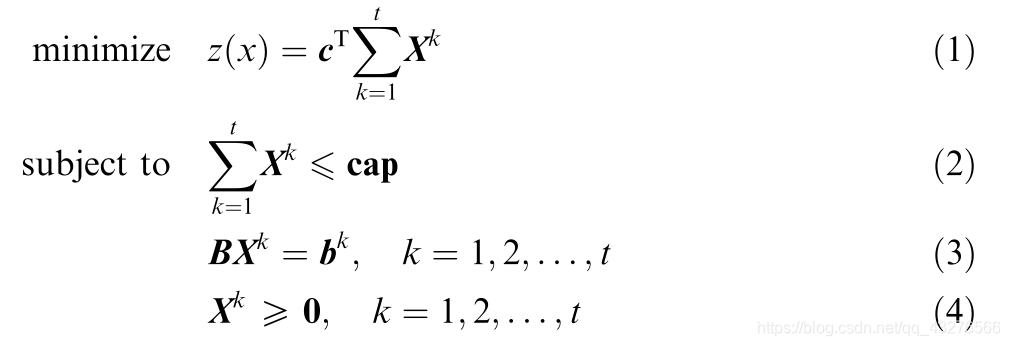
式(1)为总成本的目标函数;式(2)和(3)分别为边容量约束方程和节点流平衡方程;式(4)为非负约束。
第k中商品每条边的流量
每条边成本
每条边容量
点边关联矩阵,对于第
条边
,设
,

3 Example




该简单例子的目标函数值=43







 本文探讨了多商品流问题(MCFP),涉及网络中商品分配的复杂优化问题,通过运输需求和边容量约束求解成本最小的流量配置。文章介绍了问题定义、关键约束及一个示例,展示了如何将列生成、拉格朗日松弛等方法应用于解决实际问题。
本文探讨了多商品流问题(MCFP),涉及网络中商品分配的复杂优化问题,通过运输需求和边容量约束求解成本最小的流量配置。文章介绍了问题定义、关键约束及一个示例,展示了如何将列生成、拉格朗日松弛等方法应用于解决实际问题。
















 2653
2653

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








