微积分复习1

第一讲 函数极限与连续

本系列文章参考自《张宇高数18讲》，为了对高等数学微积分的知识进行总结而书写，本系列文章分为18个小节，本节目录见下：

• 导学
• 函数极限的定义及使用
• 函数极限的计算
• 函数极限的存在性
• 函数极限的应用

下文将根据以上内容进行讲解

refer:

1. 《张宇高数18讲》

---

1.1 导学

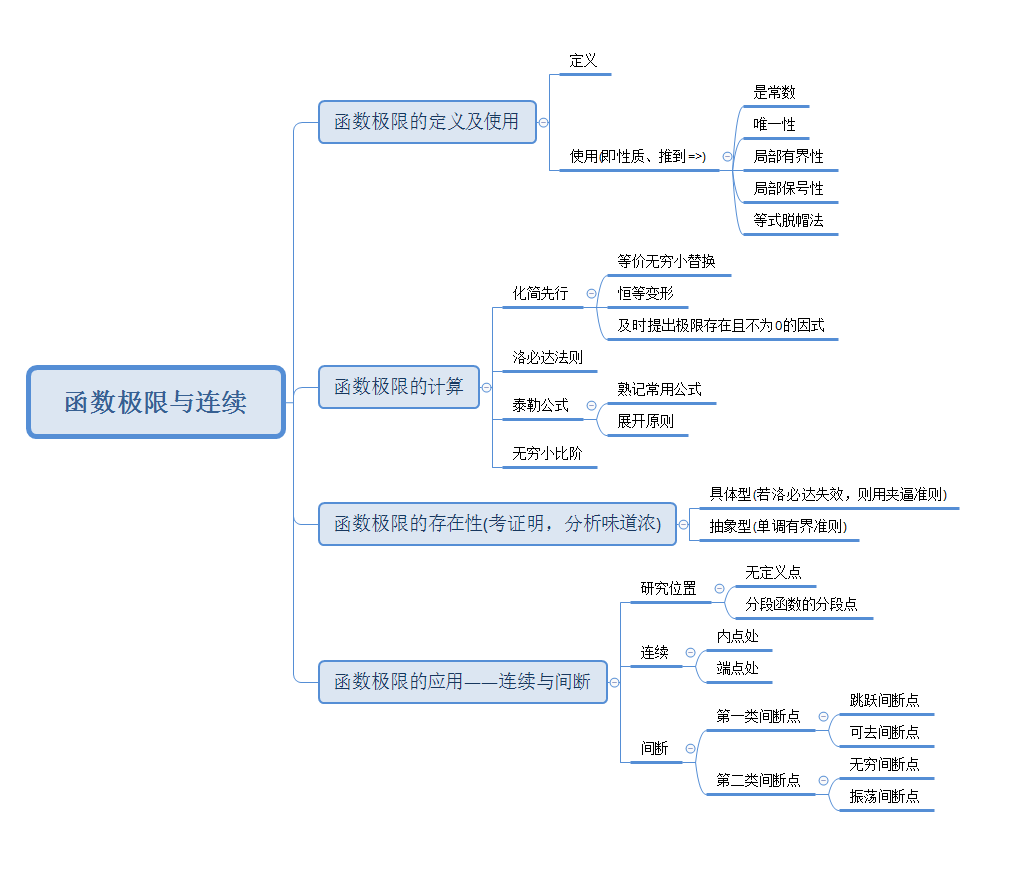
函数的极限计算是微积分的基础。该章主要从概念、计算、分析证明和应用出发，对函数极限进行讲解。思维框架导图如下：

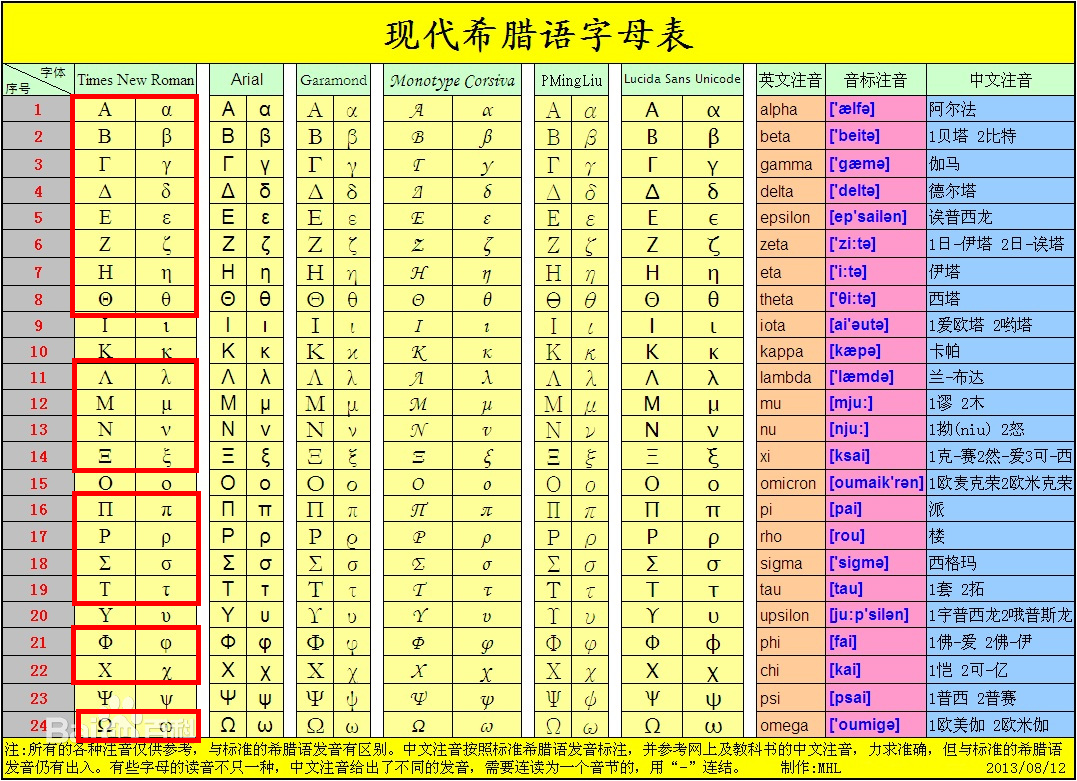
希腊字母表常见的最好记一下比如什么epsilon这些的。图中常用的已经用红色标出，最好会记会写会读能区分。

1.2 函数极限的定义及使用

1.2.1 定义

$$\underset{x\to \cdot }{\lim }f(x)=A\iff \forall \epsilon >0,x\to \cdot 时,|f(x)-A|<\epsilon$$

其中趋向分为六种情况，分别是趋向于一个数，趋向于数的左右极限，趋向于无穷，正负无穷。

1.2.2 使用

在极限存在的条件下，有5个考点，这5个也可以理解为极限存在的性质，因为由极限存在可以立马推出这5个性质。

1. 是常数
   A是一个常数，常记$$\underset{x\to \cdot }{\lim }f(x)=A$$在后面的导数、变上限积分、定积分、二重积分、三重积分存在，也都是一个常数。
2. 唯一性
   A唯一，即左极限=右极限。这个也是定义，即存在相互推到的关系：$$\underset{x\to x_0}{\lim }f(x)\exists \iff \underset{x\to x_0^{+}}{\lim }f(x)=\underset{x\to x_0^{-}}{\lim }f(x)$$
3. 局部有界性
   $$x\to \cdot 时，\exists M>0，|f(x)|\le M$$
4. 局部保号性
   $$x\to \cdot 时，若A>0\Rightarrow f(x)>0；若f(x)>0\Rightarrow A>0；$$其实是有严格的大于等于符号，为了方便记忆此处都不带等号。
5. 等式脱帽法
   $$f(x)=A+\alpha ，其中\underset{x\to \cdot }{\lim }\alpha =0$$

1.2.3 引申

一、取整函数

对于取整函数[x]，我们需要记住它的关系式$x-1<[x]\le x.$

二、函数连续的判断和性质

首先我们需要知道，

1. 初等函数指的是初等函数及初等函数经过有限次四则运算和符合得来的函数。
2. 一切初等函数在其定义区域内一定连续。（不是定义域，是定义区域）
3. 函数连续则函数值等于极限值（极限存在不一定连续，但是连续一定极限存在。如左右极限相等但不等于函数值）

三、函数有界判断

分为闭区间和开区间两种情况进行讨论

1. 若f(x)在[a,b]上连续，则f(x)在[a,b]有界
2. 若f(x)在(a,b)内连续，且在左端点的右极限存在、右端点的左极限存在（局部有界性），则f(x)在(a,b)内有界

1.3 函数极限的计算

在进行函数极限计算的时候，首先我们需要明确我们的研究对象为七种未定式，分为三组，分别是：
$\frac{0}{0},\frac{\infty }{\infty },\infty \ast 0$常用洛必达，0乘无穷常将分子分母倒代换
$\infty -\infty$通分或者倒代换创造分母再通分
${\infty }^0,0^0,1^{\infty }$常用$u^v=e^{v\ln u}$

我们可以注意到在进行函数极限计算的时候，有时候四则运算是可以拆开运算的，但是可拆性取决于拆开后两个极限都存在。

1.3.1 化简先行

一、等价无穷小替换

下列常用无穷小需要牢记，当$x\to 0时，$
$$\sin x\sim x,\tan x\sim x,\arcsin x\sim x,e^x-1\sim x,\ln (1+x)\sim x,a^x-1\sim x\ln a$$
$$1-\cos x\sim \frac{1}{2}{x}^2,(1+x{)}^{\alpha }-1\sim \alpha x$$

找带头大哥：若a和b都是同一自变量趋向过程中的无穷小量，且a = o(b)，则a+b等价于a

二、恒等变形

提取公因式
换元
通分（常和$1^{\infty }$结合）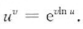

幂指
用公式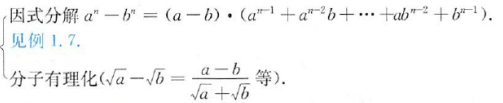

中值定理（拉格朗日——函数差值和导数关系；牛顿莱布尼茨——积分和原函数差值关系；积分中值定理——积分和函数差值关系；泰勒公式——高阶导）

三、及时提出极限存在且不为0的因式

1.3.2 洛必达法则

一、什么是洛必达法则

洛必达用于极限相除形式下，分子分母的化简，洛必达法则有三种形式，分别如下：

二、洛必达法则适用条件

洛必达法则能不能用，用了再说。

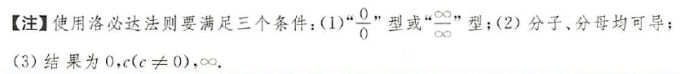
1.3.3 泰勒公式

一、什么是泰勒公式

需要熟记至少以下十种泰勒公式，其中前六种可以和无穷级数连一块记，这样记忆起来方便。注意此时都是在x0=0点处展开。

二、泰勒公式适用原则

泰勒公式展开一般有两种情况，分别是a/b和a-b，两者所遵循的原则也不一样，分别是上下同阶原则和幂次最低原则。注意此时都是在x0=0点处展开。

上下同阶原则

幂次最低原则

1.3.4 无穷小比阶

1.4 函数极限的存在性

1.4.1 具体性

当洛必达法则失效的时候常考虑夹逼准则，找出大于fx和小于fx的函数，使他们都趋向于一点，使用放缩实现：

1.4.2 抽象型

对于抽象型的函数，考虑趋向无穷极限存在与否即计算，常考虑使用单调有界准则证明函数的极限存在。
单调递增且有上界则趋向正无穷的极限存在。

1.5 函数极限的应用——连续与间断

一、研究位置

一切初等函数在其定义区间内必连续，所以对于连续和间断，我们只研究两类点，分别是无定义点（间断）和分段点。
可疑点：用于找极值的点，含驻点和导数不存在的点。
最值点：可疑点+端点。
驻点：导数为0的点。

二、判断一点是否连续

函数在该点左极限=右极限=函数值$\iff$则该点连续。
对于特定端点，如果左极限=函数值，则左连续。

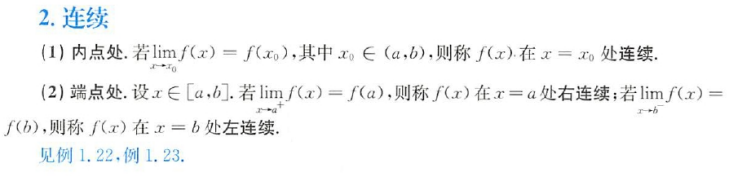
在此处（1）中，极限存在则左右极限相等等于函数极限，表达的是一个意思。

三、间断

分为4种间断点，分别是跳跃、可去、无穷、振荡。

其中第二个可去间断点在x0处极限存在，且不等于函数值。