参考文献:
1.函数的极限、连续与可导 - 期刊论文 - 道客巴巴
http://www.doc88.com/p-7478979748698.html
结论(一元函数范畴内)
可导与连续的关系:可导必连续,连续不一定可导;
可微与连续的关系:可微与可导是一样的;
可积与连续的关系:可积不一定连续,连续必定可积;
可导与可积的关系:可导一般可积,可积推不出一定可导;
①极限定义:
②连续的定义:
③可微的定义:
④可积的定义:
⑤可积与连续的关系有重要的联系:
(函数不连续的点叫做间断点)
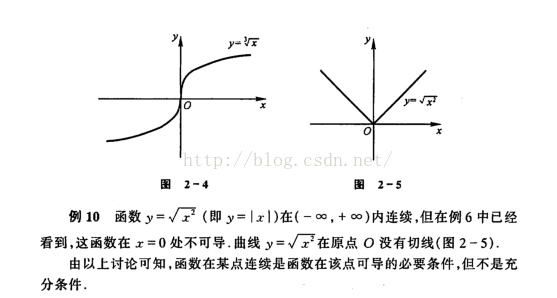
⑥可导与连续的关系:可导必连续
连续并不一定可导:
所以可微与可导是 一样的
⑧可积与连续的关系:
这个定理说明,连续的函数是可积的
这个定理说明,不连续的函数有有限个间断点的函数 也可以是可积的
所以:连续一定可积,但是可积却不一定连续;
⑨可导与可积的关系:
因为可导必定是连续的,而连续的一定可积,所以可导就一般可积(虽然可积规定要在闭区间里,但是在高等数学范围内还是可以这样认为的),可积却不一定推出可导,因为可积还有可能不连续,不连续一般是不可导的。












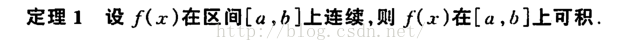




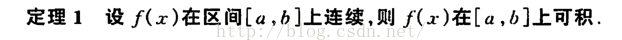















 2923
2923

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








