（深入理解）强化学习中Model-based和Model-free的区别是什么

RL的形式化

首先我们定义强化学习中的马尔可夫决策过程MDP，用四元组表示：

对于上面，我们先理解$T$，其表达了环境的不确定性，即在当前状态$s$下，我们执行一个动作$a$，其下一个状态$s^{{}^{\prime }}$是什么有很多种可能。这有点不符合我们的直觉，例如和我们通常看到的游戏可能不太一样，例如下面这个游戏（格子世界中的游戏之一：cliffwalkingv0悬崖）

你往右走一步(action)，接下来的状态就一定是如下

但是，我们试想这个例子，一只熊要吃你，假设你不是选择装死，而是选择逃跑，难道下一个状态你就一定是被吃吗？有可能你很灵活，或者跑得很快成功逃生，虽然这可能性很小。不管怎么说，当前状态是熊要吃你，你选择动作逃跑，下一个状态可能是被熊吃，也有可能是逃跑成功。

接下来，我们来理解一下那个奖励函数$R(s,a)$，因为根据上面$T$的分析，我们知道$(s,a)->s^{{}^{\prime }}$，且$s^{{}^{\prime }}$不唯一。那么问题来了，既然$s^{{}^{\prime }}$不唯一，那$R(s,a)$岂不是也不唯一？确实如此，但是我们这里的$R(s,a)$你可以理解为期望，例如10%的概率是得到奖励100，90%的概率是得到奖励10，那么期望就是19，即期望意义上，从当前状态$s$，执行这个动作$a$，得到的奖励是19。

RL求解算法

注意，环境是人设计的，环境库我们使用最多的是open AI开发的gym。

再比如上面那个悬崖游戏，是gym内置的，这个就是一个环境，而这个环境对应的强化学习MDP四元组我们人一清二楚。
因为这个游戏就是我们人设计的，哪些地方放置悬崖（黑色），哪个地方放置终点（黄色），以及奖励：踩到悬崖多少分（默认-100，可以自己设计），以及动作空间（上下左右移动），以及状态空间（48个格子）等等。

但是问题在于，玩这个游戏的不是我们人啊，是一个机器，即一个agent。他根本不知道悬崖在哪里，终点在哪里，他只知道尝试，探索，然后根据得到的反馈，比如走了一步，突然得到-100分，就估摸着可能踩到悬崖了，然后明白了，以后尽量绕道，不要走那里。

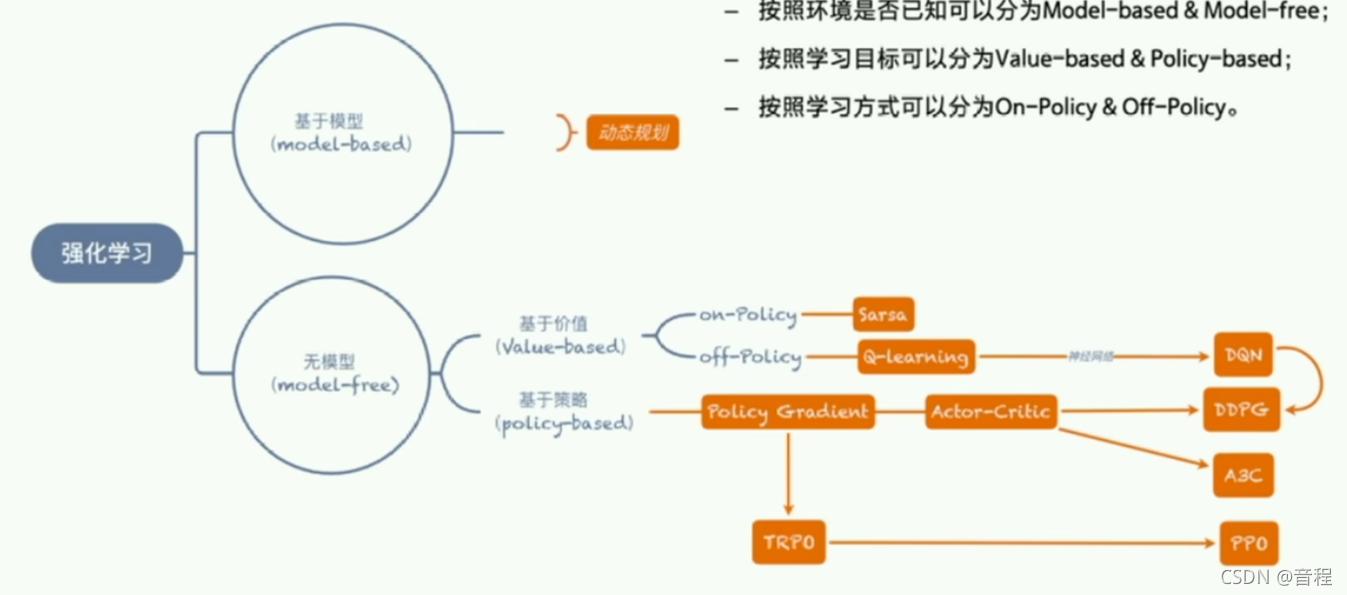
可以看到agent从一个开始乱走的小白变得越来越聪明，这从算法的角度来看，可以看作是一个求解过程，所以当然涉及求解算法（也就是强化学习算法），而这个算法可以分为Model-based和Model-free。

model-based：知己知彼，百战百胜

Model-based的思想：我们前面不是说了吗，我们人是知道环境的一切的，即那个MDP四元组，现在是机器(agent)不知道，那么求解算法就来了：把MDP四元组给求出来。怎么求？机器使用记忆（内存）保存MDP四元组，初始都初始化为空（0），然后让机器在那瞎尝试，使用MLE，即最大似然估计，慢慢填满整个MDP四元组，不断优化，去逼近真实的MDP四元组（我们人知道的那个）。举个例子，比如如果机器发现状态1往左走，每次都是状态0，那么转移概率就设置为1，即$p(0|1,left)=1$。

这就是model-based，希望重构出整个环境，对环境一清二楚之后，不就可以选择最优策略了嘛（知己知彼，百战百胜）。

Model-free：两耳不闻窗外事，一心只读圣贤书

随着强化学习的发展，人们发现，有时候我们并不需要对环境进行建模也能找到最优的策略。

model-free的思想是：我不需要通过探索恢复出环境的MDP四元组来，而是只关心$Q(s,a)$函数，即在状态$s$时执行动作$a$得到的长远性回报。注意其不同于$R(s,a)$，这个是移动完毕之后的即时回报。什么叫做长远性回报？例如救护车执行动作闯红灯，扣一分，但是因为闯红灯节省了时间，从而及时救治了一个病人加了100分，所以一共得了99分。这个扣一分就是即时回报，99分就是长远回报。

现在我们要做的就是直接估计出这个$Q$值，一步到位，不再管其他东西，也不需要保存其他人任何东西。而只需要保存下面这个表格，我们称之为$Q$表格，初始化为0，然后通过agent不断探索，尝试，采用一定的算法，慢慢填好这些数，就完成啦。这就是目标坚定的好处，正所谓：两耳不闻窗外事，一心只读圣贤书。

补充：这类方法研究得更火。

总结

在agent执行它的动作之前，它是否能对下一步的状态和回报做出预测，如果可以，那么就是model-based方法，如果不能，即为model-free方法。

来了！

---

完结撒花

---