浅谈LTI系统与卷积

参考

信号与系统（第二版）奥本海姆

系统

在开始正文之前，可以回顾一下，信号与系统的思想。实际上，系统的思想广泛存在并应用于现实世界中。比如，大学可以是一个系统，每一个学生可以视作单个输入，大学中的各类课程可以看出是系统响应，每一个年级的学生看成一个输入序列。那么，输出就可以看成，每一位学生与这个学校的所有课程做卷积的一个过程（默认大学是LTI系统），因此最终的输出结果也是一个序列。

一般来说，我们习惯于使用数学模型来描述一个系统即y=f(x)只不过这里的x在时域系统上是x=f(t)在空域系统上是x=f(n)（n可以是多维向量，用以表示多维空间的坐标）。在信号处理中，我们一般研究时域上面的系统。

LTI系统

LTI系统全称是线性时不变系统(Linear Invariant System)。在空域上即是LSI系统。显然LTI系统是一类系统其具有线性与时不变性。这对于卷积的理解至关重要。

线性即系统对于一个序列的输出满足齐次叠加原则，所以如果我们用移位脉冲序列来表示一个输入信号的话。系统的输出可以看成是每一个移位脉冲信号的输出信号的叠加。

时不变性即系统的特征不由时间的改变而改变，从数学上来说就是当输入序列为x[n-n0]输出信号就是y[n-n0]。

卷积

卷积是一种运算方式亦可以说是算子，这一运算可以被理解为对输入信号（序列）按照系统特征加权求和（离散）或加权求积（连续）。

我们先从离散时间卷积开始。

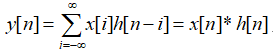
对于离散时间卷积，上述表达式可以看成，在i时刻序列x[n]输入系统H的所得到的系统响应。

初学信号与系统很容易出现的错误就是把x[n]与y[n]都看成一个数而非一个序列（只有序列才会涉及到时间轴）。

为什么在本文中一定要强调LTI系统，那是因为线性所以才符合齐次叠加原则，因为是时不变的所以i时刻的系统响应可以看成是h(n-i)。由此，卷积实际上描述了系统对于输入信号的一种运算方式。

这种方式直观的理解可以看成，序列x[n]在对系统H进行加权，输出结果是经过x[n]加权之后的序列y[n]。在LTI体系下，我们完全可以支持使用脉冲序列来理解这样一个过程。

这也就是序列x[n]从i时刻开始的每个值（i,i+1,i+2,…）乘以系统的冲击响应序列h[n]得到的所有加权序列的线性叠加的一个过程。

同理，用移位脉冲序列来解释这个过程的话。输入序列x[n]可以看成是在x[n]的加权规则下由一系列移位脉冲信号加权后线性叠加组成的。

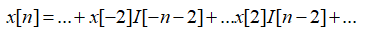
显然上述表达式可以用以下形式表示（I[n]为冲击信号）

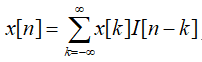
因此，在线性时不变的条件下，任何的信号都可以由一系列加权移位脉冲信号表示，同理系统的冲击响应也可以由一系列的加权移位脉冲信号表示。

不过，理解上存在难度的点，永远还是在于时间轴的存在，在LTI系统中我们不得不时时刻刻考虑时间轴。系统响应是随时间的推移改变的，所以x[n]序列的每个对应时刻的具体值就是那个时刻的权值，而那一时刻的系统响应就是待加权序列。

最终输出的序列是，所有时刻加权后的系统响应的线性叠加。

上图描述了只在三个时刻有值的信号x[n]与系统H卷积的过程。因为 x[n]只在三个时刻有具体值，因此这里我们只需要看系统H在这三个时刻的脉冲响应h_-1[n]，h₀[n]与h₁[n]即可。接下来如同所示即是，计算x[-1]对h_-1[n]的加权序列，x[0]对h₀[n]的加权序列，x[1]对h₁[n]的加权序列。再线性叠加即可得到卷积的输出结果。

总结

1. 卷积是一种在LTI特性下的运算方式，用于表示系统对输入信号的运输，结果为输出信号。
2. 卷积实际上是，基于输入信号x[n]在各个时刻的信号值（权值）对于系统h[n]在各个信号的响应序列进行加权，并且将全部时刻的加权序列线性叠加的一种运算方式。简而言之，卷积就是信号x[n]对系统响应进行加权。
3. 离散时间卷积的算术表达式还可以解释为，在i时刻，信号x[n]输入进系统H所进行的运算。