机器学习笔记
逻辑回归
简介:逻辑回归是二分类问题中的神器,非常简单和实用,是线性系统中使用率最高的模型。
逻辑回归的应用
- 预测带宽违约情况(会违约/不会违约)
- 情感分析(正面/负面)
- 预测广告点击率(会点击/不会点击)
- 预测疾病(阳性/阴性)
例如:假如我们有办法表示条件概率: P ( Y = 0 ∣ X ) 和 P ( Y = 1 ∣ X ) P(Y=0|X)和P(Y=1|X) P(Y=0∣X)和P(Y=1∣X)(其中当Y=0是负面情况,Y=1是正面情况),可以实际分类规则:
if P(y=0|X) > P(y=1|X):
y = 0
else :
y = 1
如果通过 条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)来描述X和Y之间的关系。 逻辑回归 实际上是基于线性回归模型构建起来的,所以这里也希望通过 线性回归 方程 一步步来构造上述的条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)。
逻辑函数
逻辑函数的应用非常广泛,也别是在神经网络中处处可见,很大程度上是源于它不可或缺的性质:可以把任意区间的值映射到(0,1)区间。这样的值既可以作为概率,也可以作为一种权重。另外,由于大多数模型在训练是涉及到导数(derivative)的计算,同时逻辑函数的导数具有极其简单的形态,这也使得逻辑函数收到了很大的欢迎。
y
=
1
1
+
e
−
x
定义域:
(
−
∞
,
+
∞
)
值域
(
0
,
1
)
y=\frac{1}{1+e^{-x}}\ \ \ \ \ \ \ \ \ \ \ \ 定义域:(-\infty,+\infty) \ \ \ 值域(0, 1)
y=1+e−x1 定义域:(−∞,+∞) 值域(0,1)
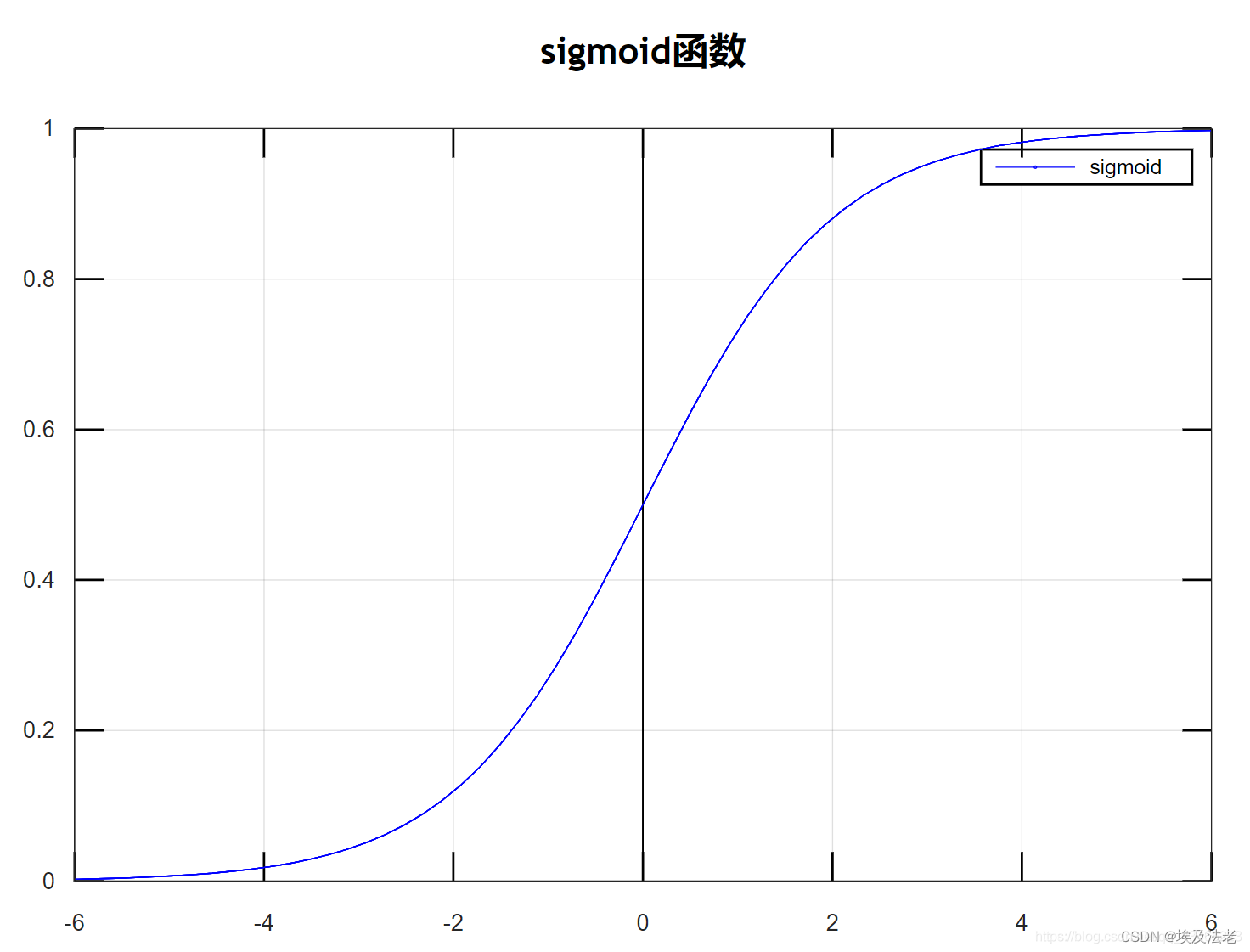
由于 P ( Y ∣ X ) 的值域在 ( 0 , 1 ) 之间,故不可以将其定义为: w T X + b 可以借助 s i g m o i d 函数,将其映射到 s i g m o i d 函数中。 即: P ( Y ∣ X ) = 1 1 + e − ( w T X + b ) 由于P(Y|X)的值域在(0,1)之间,故不可以将其定义为:w^TX+b\\ 可以借助sigmoid函数,将其映射到sigmoid函数中。\\ 即:P(Y|X)=\frac{1}{1+e^{-(w^TX+b)}} 由于P(Y∣X)的值域在(0,1)之间,故不可以将其定义为:wTX+b可以借助sigmoid函数,将其映射到sigmoid函数中。即:P(Y∣X)=1+e−(wTX+b)1
样本的条件概率
当把线性回归的式子和逻辑函数拼接在一起的时候,就可以得到合理的条件概率的表达式。
在逻辑回归中我们针对的是二分类问题,所以一个样本必须要属于其中的某一个分类。这就意味着
P
(
y
=
1
∣
x
)
和
P
(
y
=
0
∣
x
)
P(y=1|x)和P(y=0|x)
P(y=1∣x)和P(y=0∣x)之和一定会等于1。
对于特征向量
x
和二分类标签,可以定义如下条件概率:
p
(
y
=
1
∣
x
;
w
,
b
)
=
1
1
+
e
−
(
w
T
x
+
b
)
p
(
y
=
0
∣
x
;
w
,
b
)
=
e
−
(
w
T
x
+
b
)
1
+
e
−
(
w
T
x
+
b
)
可以将两个式子合并为一个式子:
p
(
y
∣
x
)
=
p
(
y
=
1
∣
x
;
w
,
b
)
y
[
1
−
p
(
y
=
1
∣
x
;
w
,
b
)
]
1
−
y
对于特征向量x和二分类标签,可以定义如下条件概率:\\ p(y=1|x;w,b)=\frac{1}{1+e^{-(w^Tx+b)}}\\ p(y=0|x;w,b)=\frac{e^{-(w^Tx+b)}}{1+e^{-(w^Tx+b)}}\\ 可以将两个式子合并为一个式子:\\ p(y|x)=p(y=1|x;w,b)^y[1-p(y=1|x;w,b)]^{1-y}
对于特征向量x和二分类标签,可以定义如下条件概率:p(y=1∣x;w,b)=1+e−(wTx+b)1p(y=0∣x;w,b)=1+e−(wTx+b)e−(wTx+b)可以将两个式子合并为一个式子:p(y∣x)=p(y=1∣x;w,b)y[1−p(y=1∣x;w,b)]1−y
逻辑函数中的目标函数
最大似然估计
最大似然估计(Maximum Likelihood Estimation)在机器学习建模中有着举足轻重的作用。他可以指引我们去构造模型的目标函数,以及求出目标函数最大或者最小的参数值。
逻辑回归的似然函数
假设我们拥有数据集
D
=
{
(
x
i
,
y
i
)
}
i
=
1
n
,
x
i
∈
R
d
,
y
i
∈
{
0
,
1
}
D=\{(x_i,y_i)\}_{i=1}^n, \ \ \ x_i ∈ R^d,y_i ∈ \{0,1\}
D={(xi,yi)}i=1n, xi∈Rd,yi∈{0,1},对于其中的任意样本
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi),我们可以定义它的似然概率
p
(
y
i
∣
x
;
w
,
b
)
=
p
(
y
i
=
1
∣
x
i
;
w
,
b
)
i
y
[
1
−
p
(
y
i
=
1
∣
x
i
;
w
,
b
)
]
1
−
y
i
p(y_i|x;w,b)=p(y_i=1|x_i;w,b)^y_i[1-p(y_i=1|x_i;w,b)]^{1-y_i}
p(yi∣x;w,b)=p(yi=1∣xi;w,b)iy[1−p(yi=1∣xi;w,b)]1−yi
逻辑回归的似然函数对于单个样本的条件概率已经定义过了,这个概率可以看做是似然概率。则所有样本的似然概率为:
P
(
D
∣
w
,
b
)
=
∏
i
=
1
n
p
(
y
i
∣
x
;
w
,
b
)
P(D|w,b)=\prod_{i=1}^np(y_i|x;w,b)
P(D∣w,b)=i=1∏np(yi∣x;w,b)
之后就需要将似然概率最大化,并求出模型的参数(对于逻辑回归就是
w
,
b
w,b
w,b)。这个过程称为最大似然估计(maximum likelihood estimation)
求解逻辑回归的参数:
w
⌢
M
L
E
,
b
⌢
M
L
E
=
a
r
g
m
a
x
w
,
b
∏
i
=
1
n
P
(
y
i
∣
x
i
;
w
,
b
)
将等式右边去对数,将乘积转换为求和
=
a
r
g
m
a
x
w
,
b
l
o
g
∏
i
=
1
n
P
(
y
i
∣
x
i
;
w
,
b
)
=
a
r
g
m
a
x
w
,
b
∑
i
=
1
n
l
o
g
P
(
y
i
∣
x
i
;
w
,
b
)
将最大值问题装换为最小值问题,只需提出一个负号
=
a
r
g
m
i
n
w
,
b
−
∑
i
=
1
n
l
o
g
P
(
y
i
∣
x
i
;
w
,
b
)
由于
p
(
y
∣
x
)
=
p
(
y
=
1
∣
x
;
w
,
b
)
y
[
1
−
p
(
y
=
1
∣
x
;
w
,
b
)
]
1
−
y
所以
w
⌢
M
L
E
,
b
⌢
M
L
E
=
a
r
g
m
i
n
w
,
b
−
∑
i
=
1
n
l
o
g
[
p
(
y
i
=
1
∣
x
i
;
w
,
b
)
y
[
1
−
p
(
y
i
=
1
∣
x
i
;
w
,
b
)
]
1
−
y
i
]
=
a
r
g
m
i
n
w
,
b
−
∑
i
=
1
n
{
y
i
l
o
g
[
p
(
y
i
=
1
∣
x
i
;
w
,
b
)
]
+
(
1
−
y
i
)
l
o
g
[
1
−
p
(
y
i
=
1
∣
x
i
;
w
,
b
)
]
}
又因为:
p
(
y
=
1
∣
x
;
w
,
b
)
=
1
1
+
e
−
(
w
T
x
+
b
)
p
(
y
=
0
∣
x
;
w
,
b
)
=
e
−
(
w
T
x
+
b
)
1
+
e
−
(
w
T
x
+
b
)
定义
σ
(
x
)
=
1
1
+
e
−
x
所以
w
⌢
M
L
E
,
b
⌢
M
L
E
=
a
r
g
m
i
n
w
,
b
−
∑
i
=
1
n
{
y
i
l
o
g
[
σ
(
w
T
x
+
b
)
]
+
(
1
−
y
i
)
l
o
g
[
1
−
σ
(
w
T
x
+
b
)
]
}
\overset{\frown} {w}_{MLE},\overset{\frown}{b}_{MLE}= argmax_{w,b}\prod_{i=1}^nP(y_i|x_i;w,b) \\ 将等式右边去对数,将乘积转换为求和 \\ =argmax_{w,b}log\prod_{i=1}^nP(y_i|x_i;w,b) \\ =argmax_{w,b}\sum_{i=1}^nlogP(y_i|x_i;w,b) \\ 将最大值问题装换为最小值问题,只需提出一个负号\\ =argmin_{w,b}-\sum_{i=1}^nlogP(y_i|x_i;w,b) \\ 由于\ \ \ \ \ \ p(y|x)=p(y=1|x;w,b)^y[1-p(y=1|x;w,b)]^{1-y} \\ 所以\ \ \ \ \ \ \overset{\frown} {w}_{MLE},\overset{\frown}{b}_{MLE}= argmin_{w,b}-\sum_{i=1}^nlog[p(y_i=1|x_i;w,b)^y[1-p(y_i=1|x_i;w,b)]^{1-y_i} ]\\ = argmin_{w,b}-\sum_{i=1}^n\{y_ilog[p(y_i=1|x_i;w,b)]+(1-y_i)log[1-p(y_i=1|x_i;w,b)]\} \\ 又因为 :p(y=1|x;w,b)=\frac{1}{1+e^{-(w^Tx+b)}}\\ p(y=0|x;w,b)=\frac{e^{-(w^Tx+b)}}{1+e^{-(w^Tx+b)}}\\ 定义\sigma(x) =\frac{1}{1+e^{-x}} \\ 所以\overset{\frown} {w}_{MLE},\overset{\frown}{b}_{MLE} = argmin_{w,b}-\sum_{i=1}^n\{y_ilog[\sigma(w^Tx+b)]+(1-y_i)log[1-\sigma(w^Tx+b)]\} \\
w⌢MLE,b⌢MLE=argmaxw,bi=1∏nP(yi∣xi;w,b)将等式右边去对数,将乘积转换为求和=argmaxw,blogi=1∏nP(yi∣xi;w,b)=argmaxw,bi=1∑nlogP(yi∣xi;w,b)将最大值问题装换为最小值问题,只需提出一个负号=argminw,b−i=1∑nlogP(yi∣xi;w,b)由于 p(y∣x)=p(y=1∣x;w,b)y[1−p(y=1∣x;w,b)]1−y所以 w⌢MLE,b⌢MLE=argminw,b−i=1∑nlog[p(yi=1∣xi;w,b)y[1−p(yi=1∣xi;w,b)]1−yi]=argminw,b−i=1∑n{yilog[p(yi=1∣xi;w,b)]+(1−yi)log[1−p(yi=1∣xi;w,b)]}又因为:p(y=1∣x;w,b)=1+e−(wTx+b)1p(y=0∣x;w,b)=1+e−(wTx+b)e−(wTx+b)定义σ(x)=1+e−x1所以w⌢MLE,b⌢MLE=argminw,b−i=1∑n{yilog[σ(wTx+b)]+(1−yi)log[1−σ(wTx+b)]}
因此得到了一个化简之后的目标函数:
w
⌢
M
L
E
,
b
⌢
M
L
E
=
a
r
g
m
i
n
w
,
b
−
∑
i
=
1
n
{
y
i
l
o
g
[
σ
(
w
T
x
+
b
)
]
+
(
1
−
y
i
)
l
o
g
[
1
−
σ
(
w
T
x
+
b
)
]
}
\overset{\frown} {w}_{MLE},\overset{\frown}{b}_{MLE} = argmin_{w,b}-\sum_{i=1}^n\{y_ilog[\sigma(w^Tx+b)]+(1-y_i)log[1-\sigma(w^Tx+b)]\}
w⌢MLE,b⌢MLE=argminw,b−i=1∑n{yilog[σ(wTx+b)]+(1−yi)log[1−σ(wTx+b)]}
接下来需要使用到梯度下降法进行优化。
梯度下降法
常见的函数优化中常见的有两种算法:
- 把导数设为0
- 基于迭代式的算法来求解,如梯度下降法
求函数的最大值/最小值
第一种方法我们也称之为解析解(Analytic Solution)。但这里需要注意的一点是并不是所有的,目标函数都可以通过吧导数设为零的方式来求解的。
假设有函数
f
(
x
)
,求使得
f
(
x
)
值最小的参数
x
,可根据如下梯度下降法来求解最优解
x
初始化
x
1
f
o
r
t
=
1
,
2
,
3
,
.
.
.
x
t
+
1
=
x
t
−
η
∇
f
(
x
t
)
假设有函数f(x),求使得f(x)值最小的参数x,可根据如下 梯度下降法来求解最优解x\\ 初始化x^1\\ for\ \ \ t = 1,2,3,...\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x^{t+1} = x^{t} - \eta\nabla f(x^t)
假设有函数f(x),求使得f(x)值最小的参数x,可根据如下梯度下降法来求解最优解x初始化x1for t=1,2,3,... xt+1=xt−η∇f(xt)
对于梯度下降法来说,有一个重要的参数叫作学习率(learning rate), 可以把它看作是可调节的参数(也称之为超参数)。学习率对于收敛以及对最终的结果起到很重要的作用。
- 当学习率比较小时,收敛会比较慢
- 当学习率很大时,算法不稳定,有可能不收敛
对sigmoid函数求导:
σ
(
x
)
=
1
1
+
e
−
x
σ
′
(
x
)
=
e
−
x
(
1
+
e
−
x
)
2
=
σ
(
x
)
[
1
−
σ
(
x
)
]
\sigma(x) =\frac{1}{1+e^{-x}} \\ \sigma^{'}(x)=\frac{e^{-x}}{(1+e^{-x})^2}\\ =\sigma(x)[1-\sigma(x)]
σ(x)=1+e−x1σ′(x)=(1+e−x)2e−x=σ(x)[1−σ(x)]
逻辑回归的梯度下降法
设 l ( w , b ) = − ∑ i = 1 n { y i l o g [ σ ( w T x + b ) ] + ( 1 − y i ) l o g [ 1 − σ ( w T x + b ) ] } 设l(w,b) =-\sum_{i=1}^n\{y_ilog[\sigma(w^Tx+b)]+(1-y_i)log[1-\sigma(w^Tx+b)]\}\\ 设l(w,b)=−i=1∑n{yilog[σ(wTx+b)]+(1−yi)log[1−σ(wTx+b)]}
①求解
w
w
w:
∂
l
(
w
,
b
)
∂
w
=
−
∑
i
=
1
n
y
i
σ
(
w
T
x
i
+
b
)
[
1
−
σ
(
w
T
x
i
+
b
)
]
x
i
σ
(
w
T
x
i
+
b
)
+
(
1
−
y
i
)
−
σ
(
w
T
x
i
+
b
)
[
1
−
σ
(
w
T
x
i
+
b
)
]
x
i
1
−
σ
(
w
T
x
i
+
b
)
=
−
∑
i
=
1
n
y
i
[
1
−
σ
(
w
T
x
i
+
b
)
]
x
i
+
(
y
i
−
1
)
σ
(
w
T
x
i
+
b
)
x
i
=
−
∑
i
=
1
n
[
y
i
−
y
i
σ
(
w
T
x
i
+
b
)
+
y
i
σ
(
w
T
x
i
+
b
)
−
σ
(
w
T
x
i
+
b
)
]
x
i
=
−
∑
i
=
1
n
[
y
i
−
σ
(
w
T
x
i
+
b
)
]
x
i
=
∑
i
=
1
n
[
σ
(
w
T
x
i
+
b
)
−
y
i
]
x
i
\frac{ \partial l(w,b)}{ \partial w} = -\sum_{i=1}^ny_i\frac{\sigma(w^Tx_i+b)[1-\sigma(w^Tx_i+b)]x_i}{\sigma(w^Tx_i+b)}+(1-y_i)\frac{-\sigma(w^Tx_i+b)[1-\sigma(w^Tx_i+b)]x_i}{1-\sigma(w^Tx_i+b)}\\ =-\sum_{i=1}^ny_i[1-\sigma(w^Tx_i+b)]x_i+(y_i-1)\sigma(w^Tx_i+b)x_i\\ =-\sum_{i=1}^n[y_i-y_i\sigma(w^Tx_i+b)+y_i\sigma(w^Tx_i+b)-\sigma(w^Tx_i+b)]x_i\\ =-\sum_{i=1}^n[y_i-\sigma(w^Tx_i+b)]x_i\\ =\sum_{i=1}^n[\sigma(w^Tx_i+b)-y_i]x_i
∂w∂l(w,b)=−i=1∑nyiσ(wTxi+b)σ(wTxi+b)[1−σ(wTxi+b)]xi+(1−yi)1−σ(wTxi+b)−σ(wTxi+b)[1−σ(wTxi+b)]xi=−i=1∑nyi[1−σ(wTxi+b)]xi+(yi−1)σ(wTxi+b)xi=−i=1∑n[yi−yiσ(wTxi+b)+yiσ(wTxi+b)−σ(wTxi+b)]xi=−i=1∑n[yi−σ(wTxi+b)]xi=i=1∑n[σ(wTxi+b)−yi]xi
接下来使用梯度下降法求解
w
w
w
②求解
b
b
b:
∂
l
(
w
,
b
)
∂
b
=
−
∑
i
=
1
n
[
y
i
σ
(
w
T
x
i
+
b
)
[
1
−
σ
(
w
T
x
i
+
b
)
]
σ
(
w
T
x
i
+
b
)
+
(
1
−
y
i
)
−
σ
(
w
T
x
i
+
b
)
[
1
−
σ
(
w
T
x
i
+
b
)
]
1
−
σ
(
w
T
x
i
+
b
)
]
=
−
∑
i
=
1
n
[
y
i
[
1
−
σ
(
w
T
x
i
+
b
)
]
+
(
y
i
−
1
)
σ
(
w
T
x
i
+
b
)
]
=
−
∑
i
=
1
n
[
y
i
−
y
i
σ
(
w
T
x
i
+
b
)
+
y
i
σ
(
w
T
x
i
+
b
)
−
σ
(
w
T
x
i
+
b
)
]
=
∑
i
=
1
n
[
σ
(
w
T
x
i
+
b
)
−
y
i
]
\frac{ \partial l(w,b)}{ \partial b} = -\sum_{i=1}^n[y_i\frac{\sigma(w^Tx_i+b)[1-\sigma(w^Tx_i+b)]}{\sigma(w^Tx_i+b)}+(1-y_i)\frac{-\sigma(w^Tx_i+b)[1-\sigma(w^Tx_i+b)]}{1-\sigma(w^Tx_i+b)}]\\ =-\sum_{i=1}^n[y_i[1-\sigma(w^Tx_i+b)]+(y_i-1)\sigma(w^Tx_i+b)]\\ =-\sum_{i=1}^n[y_i-y_i\sigma(w^Tx_i+b)+y_i\sigma(w^Tx_i+b)-\sigma(w^Tx_i+b)]\\ =\sum_{i=1}^n[\sigma(w^Tx_i+b)-y_i]
∂b∂l(w,b)=−i=1∑n[yiσ(wTxi+b)σ(wTxi+b)[1−σ(wTxi+b)]+(1−yi)1−σ(wTxi+b)−σ(wTxi+b)[1−σ(wTxi+b)]]=−i=1∑n[yi[1−σ(wTxi+b)]+(yi−1)σ(wTxi+b)]=−i=1∑n[yi−yiσ(wTxi+b)+yiσ(wTxi+b)−σ(wTxi+b)]=i=1∑n[σ(wTxi+b)−yi]
接下来使用梯度下降法求解b
③逻辑回归的梯度下降法
随机初始化
w
1
,
b
1
f
o
r
t
=
1
,
2
,
.
.
.
w
t
+
1
=
w
t
−
η
t
∑
i
=
1
n
[
σ
(
w
t
T
x
i
+
b
t
)
x
i
]
b
t
+
1
=
b
t
−
η
t
∑
i
=
1
n
[
σ
(
w
t
T
x
i
+
b
t
)
]
随机初始化w^1,b^1\\ for\ t = 1,2,...\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ w^{t+1}=w^t-\eta_t\sum_{i=1}^n[\sigma({w^{t}}^Tx_i+b^t)x_i]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b^{t+1}=b^t-\eta_t\sum_{i=1}^n[\sigma({w^{t}}^Tx_i+b^t)]
随机初始化w1,b1for t=1,2,... wt+1=wt−ηti=1∑n[σ(wtTxi+bt)xi] bt+1=bt−ηti=1∑n[σ(wtTxi+bt)]
梯度下降法过程中
- 如果在相邻两个时间段损失函数没有任何变化或者变化很小,即可以认为优化过程已收敛
- 如果在相邻两个时间段参数的值没有变化或者变化很小,即可以认为优化过程已收敛
梯度下降法的缺点:当样本很多的时候,每一次迭代所花费的时间成本是很高的。
随机梯度下降法
随机梯度下降法(SGD):可以看作是梯度下降法的极端的情况。在梯度下降法里,每次的参数更新依赖于所有的样本。然而,在随机梯度下降法里,每一次的迭代不再依赖于所有样本的梯度之和,而是仅仅依赖于其中一个样本的 梯度 。所以这种方法的优势很明显,通过很“便宜”的方式获得梯度,并频繁的对参数做迭代更新,这有助于在更短的时间内得到收敛结果。
SGD的一大缺点就是计算出的梯度包含很多噪音。 实际上,SGD的收敛效率通常是更高的,而且有些时候SGD的最后找出来的解更优质。
迭代不再依赖于所有样本的梯度之和,而是仅仅依赖于其中一个样本的 梯度 。所以这种方法的优势很明显,通过很“便宜”的方式获得梯度,并频繁的对参数做迭代更新,这有助于在更短的时间内得到收敛结果。
SGD的一大缺点就是计算出的梯度包含很多噪音。 实际上,SGD的收敛效率通常是更高的,而且有些时候SGD的最后找出来的解更优质。


























 1399
1399











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










