动态规划之4种背包问题

最新推荐文章于 2024-06-02 18:51:22 发布
最新推荐文章于 2024-06-02 18:51:22 发布
阅读量341 收藏
点赞数
分类专栏： 数据结构与算法 文章标签： 动态规划 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_43478694/article/details/125815932
版权

文章目录

1. 0-1背包

给定n 种物品，每种物品都有重量 w i w_i wi​和价值 v i v_i vi​，每种物品都只有一个。另外，背包容量为W 。求解在不超过背包容量的情况下将哪些物品放入背包，才可以使背包中的物品价值之和最大。每种物品只有一个，要么不放入（0），要么放入（1），因此称之为01背包

c [i ][j]表示将前i 种物品放入容量为j 的背包中获得的最大价值

第i种物品有两种选择：

  1. 不放入：放入背包的价值不增加，问题转化为“将前i -1种物品放入容量为j 的背包中获得的最大价值”，最大价值为c [i -1][j ]
  2. 放入：在第i 种物品放入之前为第i -1阶段，相当于从第i -1阶段向第i 阶段转化。问题转化为“将前i -1种物品放入容量为j -w [i ]的背包中获得的最大价值”，此时获得的最大价值就是 c [i -1][j -w [i ]]，再加上放入第i 种物品获得的价值v [i ]，总价值为c [i -1][j -w [i ]]+v [i ]

若背包容量不足，则肯定不可以放入，所以价值仍为前i- 1种物品处理后的结果；若背包容量充足，则考察在放入、不放入哪种情况下获得的价值更大, 状态转移方程如下：

c [ i ] [ j ] = { c [ i − 1 ] [ j ] , j<w[i] 当前背包剩余容量不能放下物品i m a x ( c [ i − 1 ] [ j − w [ i ] ] + v [ i ] , c [ i − 1 ] [ j ] ) , 当前背包剩余容量能放下物品i,可以选择放也可以选择不放 c[i][j]= \begin{cases} c[i-1][j], & \text{j<w[i] 当前背包剩余容量不能放下物品i} \\ max(c[i-1][j-w[i]]+v[i],c[i-1][j]), & \text{当前背包剩余容量能放下物品i,可以选择放也可以选择不放} \\ \end{cases} c[i][j]={c[i−1][j],max(c[i−1][j−w[i]]+v[i],c[i−1][j]),​j<w[i] 当前背包剩余容量不能放下物品i当前背包剩余容量能放下物品i,可以选择放也可以选择不放​

public void zeroOneBackpack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int n=w.length;
		int W=10;
		int[][]c=new int[n+1][W+1];
		//初始化第一列为0 背包容量为0-->价值为0
		for(int i=0;i<=n;i++) {
			c[i][0]=0;
		}
		//初始化第一行为0 物品个数为0-->价值为0
		for(int j=0;j<=W;j++) {
			c[0][j]=0;
		}
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=W;j++) {
				if(w[i-1]>j) {//当前物品i太重了 背包容量不足 因为下标从0开始 w[i-1]表示的的第i个物品
					c[i][j]=c[i-1][j];
				}else {
					c[i][j]=Math.max(c[i-1][j],c[i-1][j-w[i-1]]+v[i-1]);
				}
			}
		}
		System.out.println("max value: "+c[n][W]);
		
		//逆向构造最优解
		int[] x=new int[n+1];//x[i]=1说明第i个物品被放入背包中
		int j=W;
		for(int i=n;i>=1;i--) {
			if(c[i][j]>c[i-1][j]) {//c [i][j]>c [i−1][j]，则说明第i种物品被放入背包
				x[i]=1;
				j-=w[i-1];
			}else{
				x[i]=0;
			}
		}
		
		System.out.println("放入背包中的物品：");
		for(int i=1;i<=n;i++) {
			if(x[i]==1) {
				System.out.println("v["+(i-1)+"]="+v[i-1]);
			}
		}
	}

算法优化：

当处理第i 种物品时，只需第i -1种物品的处理结果，若不需要构造最优解，则放入第i -1种物品之前的处理结果已经没用了

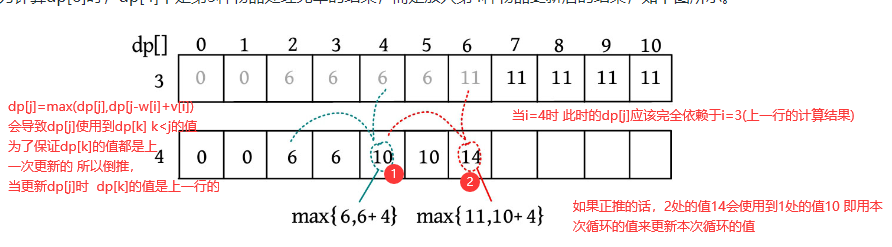
dp[j ]表示将物品放入容量为j 的背包中可以获得的最大价值， 这里的第二层循环需要倒退W, 正推会导致某个物品被选中不止一次，不满足0-1背包的条件，
在这里插入图片描述

public void zeroOneBackpack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int n=w.length;
		int W=10;
		int[] dp=new int[W+1];
		for(int i=1;i<=n;i++) {
			for(int j=W;j>=w[i-1];j--) {//j>=w[i-1]:当前容量能放下物品i
				dp[j]=Math.max(dp[j], dp[j-w[i-1]]+v[i-1]);
			}
		}
		System.out.println("max value: "+dp[W]);	
	}

2. 完全背包

给定n 种物品，每种物品都有重量 w i w_i wi​和价值 v i v_i vi​，其数量没有限制。背包容量为W ，求解在不超过背包容量的情况下如何放置物品，使背包中物品的价值之和最大

public void knapsack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int n=w.length;
		int W=10;
		int[][]c=new int[n+1][W+1];
		//初始化第一列为0 背包容量为0-->价值为0
		for(int i=0;i<=n;i++) {
			c[i][0]=0;
		}
		//初始化第一行为0 物品个数为0-->价值为0
		for(int j=0;j<=W;j++) {
			c[0][j]=0;
		}
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=W;j++) {
				for(int k=0;k*w[i-1]<=j;k++) {//第i个物品可能被选中多次 只要不超过背包容量
					c[i][j]=Math.max(c[i][j],c[i-1][j-k*w[i-1]]+k*v[i-1]);
					//c[i-1][j]  不选择当前物品i
					//c[i-1][j-k*w[i-1]]+k*v[i-1] 选择k个当前物品i
					//容量判断在k*w[i-1]<=j体现
				}
					
			}
		}
		System.out.println("max value: "+c[n][W]);
		// 逆向构造最优解
		int[] x=new int[n+1];
		int i=n,j=W;
		while(i>0&&j>0) {
			if(j-w[i-1]>=0&&c[i][j]==c[i][j-w[i-1]]+v[i-1]) {
				j-=w[i-1];//同一种物品可能被加入多次 可以是在同一行 c[i][j]和c[i][j-v]的状态有关
				x[i]++;
			}else {//c[i][j]=c[i-1][j]才能说明背包里面不会含有i
				i--;
			}
		}

		System.out.println("放入背包中的物品：");
		for (i = 1; i <= n; i++) {
			while(x[i]-->0) {
				System.out.println("v[" + (i - 1) + "]=" + v[i - 1]+"  w[" + (i - 1) + "]=" + w[i - 1]);
			}
		}
	}

和0-1背包优化的思路一样，完全背包也可以使用一维数组进行滚动：

public void knapsack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int n=w.length;
		int W=10;
		int[] dp=new int[W+1];
		for(int i=1;i<=n;i++) {
			for(int j=w[i-1];j<=W;j++) {//j>=w[i-1]:当前容量能放下物品i
				dp[j]=Math.max(dp[j], dp[j-w[i-1]]+v[i-1]);
			}
		}
		System.out.println("max value: "+dp[W]);	
	
		
	}

完全背包也可以转化为0-1背包问题，假设某个物品重量为w, 背包容量为W，则该物品最多出现W/w（向下取整）次，即将一个重量为w物品看成W/w（向下取整）个重量为w的物品，然后按照0-1背包进行处理

3. 多重背包

给定n 种物品，每种物品都有重量 w i w_i wi​和价值 v i v_i vi​ ，每种物品的数量都可以大于1但是有限制。第i 种物品有ci 个。背包容量为W ，求解在不超过背包容量的情况下如何放置物品，可以使背包中物品的价值之和最大。我们可以将多重背包问题通过暴力拆分或二进制拆分转化为01背包问题，也可以通过数组优化对物品数量进行限制

1. 暴力拆分
将第i 种物品看作ci 种独立的物品，每种物品只有一个，转化为01背包问题

public void knapsack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int[] limit= {1,2,3,4,5};
		int n=w.length;
		int W=10;
		int[][]c=new int[n+1][W+1];
		//初始化第一列为0 背包容量为0-->价值为0
		for(int i=0;i<=n;i++) {
			c[i][0]=0;
		}
		//初始化第一行为0 物品个数为0-->价值为0
		for(int j=0;j<=W;j++) {
			c[0][j]=0;
		}
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=W;j++) {
				for(int k=0;k*w[i-1]<=j&&k<=limit[i-1];k++) {//第i个物品:最多被选中limit[i-1]次并且不能超过背包容量
					c[i][j]=Math.max(c[i][j],c[i-1][j-k*w[i-1]]+k*v[i-1]);
					//c[i-1][j]  不选择当前物品i
					//c[i-1][j-k*w[i-1]]+k*v[i-1] 选择k个当前物品i
					//容量判断在k*w[i-1]<=j体现
				}
					
			}
		}
		System.out.println("max value: "+c[n][W]);
	// 逆向构造最优解
		int[] x=new int[n+1];
		int i=n,j=W;
		while(i>0&&j>0) {
			if(j-w[i-1]>=0&&c[i][j]==c[i][j-w[i-1]]+v[i-1]) {
				j-=w[i-1];//同一种物品可能被加入多次 可以是在同一行 c[i][j]和c[i][j-v]的状态有关
				x[i]++;
			}else {//c[i][j]=c[i-1][j]才能说明背包里面不会含有i
				i--;
			}
		}

		System.out.println("放入背包中的物品：");
		for (i = 1; i <= n; i++) {
			while(x[i]-->0) {
				System.out.println("v[" + (i - 1) + "]=" + v[i - 1]+"  w[" + (i - 1) + "]=" + w[i - 1]);
			}
		}
		
	}

一维数组优化：

public void knapsack() {
		int[] w = { 2, 5, 4, 2, 3 };
		int[] v = { 6, 3, 5, 4, 6 };
		int[] limit = { 1, 2, 3, 4, 5 };
		int n = w.length;
		int W = 10;
		int[] dp=new int[W+1];
 		for(int i=1;i<=n;i++) {
			for(int k=1;k<=limit[i-1];k++) {
				for(int j=W;j>=w[i-1];j--) {//j>=w[i-1]:当前容量能放下物品i
					dp[j]=Math.max(dp[j], dp[j-w[i-1]]+v[i-1]);
				}
			}
		}
		System.out.println("max value: "+dp[W]);	

	}

2. 二进制拆分
在这里插入图片描述

public void knapsack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int[] limit= {1,2,3,4,5};
		int n=w.length;
		int W=10;
		int[] dp=new int[W+1];
		for(int i=1;i<=n;i++) {
			if(limit[i-1]*w[i-1]>=W) {//转化为完全背包问题 第i个物品即使使得背包容量满了也不会超出数量限制
				for(int j=w[i-1];j<=W;j++) {
					dp[j]=Math.max(dp[j],dp[j-w[i-1]]+v[i-1]);
				}
			}else {
				for(int k=1;limit[i-1]>0;k<<=1) {
					int x=Math.min(k,limit[i-1]);//k>=limit[i-1] x=1 2 4 ... 否则就是剩余的r
					for(int j=W;j>=w[i-1]*x;j--) {
						dp[j]=Math.max(dp[j],dp[j-w[i-1]*x]+v[i-1]*x);
					}
					limit[i-1]-=x;//本次选中了x个物品i
				}
			}
		}
		System.out.println("max value: "+dp[W]);
	

	}

3. 数组优化

num[j ]数组记录容量为j 时放入了多少个第i 种物品，以满足物品数量限制

public void knapsack() {
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		int[] limit= {1,2,3,4,5};
		int n=w.length;
		int W=10;
		int[] dp=new int[W+1];
		for(int i=1;i<=n;i++) {
			int[] num=new int [W+1];
			for(int j=w[i-1];j<=W;j++) {
				if(dp[j]<dp[j-w[i-1]]+v[i-1]&&num[j-w[i-1]]<limit[i-1]) {
					dp[j]=dp[j-w[i-1]]+v[i-1];
					num[j]=num[j-w[i-1]]+1;
				}
			}
		}
		System.out.println("max value: "+dp[W]);
	

	}

4. 分组背包

给定n 组物品，第i 组有 c i c_i ci​个物品，第i 组的第j 个物品有重量 w i j w_{ij} wij​ 和价值 v i j v_{ij} vij​ ，背包容量为W ，在不超过背包容量的情况下每组最多选择一个物品，求解如何放置物品可使背包中物品的价值之和最大

c [i ][j ]表示将前i 组物品放入容量为j 的背包中可以获得的最大价值

  1. 若不放入第i 组物品，则放入背包的价值不增加，问题转化为“将前i −1组物品放入容量为j 的背包中可以获得的最大价值”，最大价值为c [i -1][j ]

  2. 若放入第i 组的第k 个物品，则相当于从第i -1阶段向第i 阶段转移，问题转化为“将前i −1组物品放入容量为j -w [i ][k ]的背包中可以获得的最大价值”，此时获得的最大价值是c [i -1][j -w [i ][k ]]，再加上放入第i 组的第k 个物品获得的价值v [i ][k ]，总价值为c [i -1][j -w [i ][k ]]+v [i ][k ]

    c [ i ] [ j ] = { c [ i − 1 ] [ j ] , j<w[i][k] m a x ( c [ i − 1 ] [ j − w [ i ] [ k ] ] + v [ i ] [ k ] , c [ i − 1 ] [ j ] ) , 1 < = k < = l i m i t [ i ] 当前背包剩余容量能放下物品i,可以选择放也可以选择不放 c[i][j]= \begin{cases} c[i-1][j], & \text{j<w[i][k]} \\ max(c[i-1][j-w[i][k]]+v[i][k],c[i-1][j]), 1<=k<=limit[i]& \text{当前背包剩余容量能放下物品i,可以选择放也可以选择不放} \\ \end{cases} c[i][j]={c[i−1][j],max(c[i−1][j−w[i][k]]+v[i][k],c[i−1][j]),1<=k<=limit[i]​j<w[i][k]当前背包剩余容量能放下物品i,可以选择放也可以选择不放​

public void knapsack() {
		int[][] w = { { 1, 2, 3, 4, 5 }, { 3, 5, 6, 1, 7 }, { 1, 7, 9, 2, 4 } };
		int[][] v = { { 1, 2, 2, 3, 1 }, { 4, 1, 3, 5, 1 }, { 1, 3, 2, 1, 3 } };
		int n = w.length;
		int W = 10;

		int[][] c = new int[n + 1][W + 1];
		// 初始化第一列为0 背包容量为0-->价值为0
		for (int i = 0; i <= n; i++) {
			c[i][0] = 0;
		}
		// 初始化第一行为0 物品个数为0-->价值为0
		for (int j = 0; j <= W; j++) {
			c[0][j] = 0;
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= W; j++) {

				for (int k = 1; k <= w[i - 1].length; k++) {
					int tmp;// 使用一个临时变量 防止c[i][j]已经得到最大值后又被较小值覆盖
					if (j < w[i - 1][k - 1]) {
						tmp = c[i - 1][j];
					} else {
						tmp = Math.max(c[i - 1][j], c[i - 1][j - w[i - 1][k - 1]] + v[i - 1][k - 1]);
					}
					if (tmp > c[i][j]) {
						c[i][j] = tmp;
					}
				}
			}
		}
		System.out.println("max value: " + c[n][W]);
		// 逆向构造最优解
		int[][] x = new int[3 + 1][5 + 1];// x[i]=1说明第i个物品被放入背包中
		int j = W;
		for (int i = 3; i >= 1; i--) {
			if (c[i][j] > c[i - 1][j]) {// c [i][j]>c [i−1][j]，则说明第i组中有物品被放入背包
				for (int k = 1; k <= w[i - 1].length; k++) {// 找出是第i组中的哪个物品
					if (c[i][j] == c[i - 1][j-w[i - 1][k - 1]] + v[i - 1][k - 1]) {// 第i组的第k个物品被选中
						x[i][k] = 1;
						j -= w[i - 1][k - 1];
						break;
					}
				}
			}
		}

		System.out.println("放入背包中的物品：");
		for (int i = 1; i <= 3; i++) {
			for (j = 1; j <= 5; j++) {
				if (x[i][j] == 1) {
					System.out.println("v[" + (i - 1) + "]=" + v[i - 1][j - 1]);
				}
			}
		}

	}

一维数组优化：

public void knapsack() {
		int[][] w = { { 1, 2, 3, 4, 5 }, { 3, 5, 6, 1, 7 }, { 1, 7, 9, 2, 4 } };
		int[][] v = { { 1, 2, 2, 3, 1 }, { 4, 1, 3, 5, 1 }, { 1, 3, 2, 1, 3 } };
		int n = w.length;
		int W = 10;
		int[]dp=new int[W+1];
		for (int i = 1; i <= n; i++) {
			for(int j=W;j>=0;j--) {
				for(int k=1;k<=w[i-1].length;k++) {
					if(j>=w[i-1][k-1]) {
						dp[j]=Math.max(dp[j],dp[j-w[i-1][k-1]]+v[i-1][k-1]);
					}
				}
			}
		}
		System.out.println("max value: " + dp[W]);

	}

参考：《算法训练营-高级篇》

CodePanda@GPF
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 0
    评论
专栏目录
动态规划——背包问题整理（01背包+完全背包）
weixin_50666824的博客
02-15 6904
1、引言 背包问题简单描述，其实就是有一堆物品同时具有一定价值和重量，现有一个背包可以承受最大重量m，那么要怎么选择在不超过背包最大重量的前提下，使背包中选择的物品价值最大。 最常见的背包问题又可以分为：01背包和完全背包，图示如下： （图片引自：代码随想录） 2、标准01背包分析 （1）问题描述 （2）分析 最直接的想法应该是暴力解法，每一件物品只存在两种状态，拿或者不拿，那么便可以采用回溯的思想例举出所有可能，然后找到价值最大的组合，但我们会发现时间复杂度就到了...
动态规划专题之多重背包问题1
08-08
动态规划是一种解决问题的有效方法，尤其在处理资源有限但选择众多的问题时。在本文中，我们将深入探讨一个具体的动态规划问题，即多重背包问题。多重背包问题与经典的0-1背包问题有所不同，它允许每种物品可以被...
动态规划之背包问题
m0_64226820的博客
07-26 8679
动态规划的背包问题总结
动态规划——0/1背包问题(全网最细+图文解析)
热门推荐
Biteht的博客
05-08 6万+
01背包你真的掌握了吗?进来带你10分钟秒杀
动态规划算法：背包问题
最新发布
2301_79881188的博客
06-02 1106
背包问题概述背包问题概述背包问题 (Knapsack problem) 是⼀种组合优化的NP完全问题。问题可以描述为：给定⼀组物品，每种物品都有⾃⼰的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最⾼。根据物品的个数，分为如下⼏类：•01 背包问题：每个物品只有⼀个•完全背包问题：每个物品有⽆限多个•多重背包问题：每件物品最多有 si 个•混合背包问题：每个物品会有上⾯三种情况......•。
背包问题算法全解析：动态规划和贪心算法详解
BASK2312的博客
04-28 3973
计算机背包问题是动态规划算法中的经典问题。本文将从理论和实践两个方面深入探讨计算机背包问题，并通过实际案例分析，帮助读者更好地理解和应用该问题。
【动态规划】背包问题题型及方法归纳
STAR GAME
02-16 5453
背包问题是在规定背包容量为j的前提下，每个物品对应的体积为v[i]，价值为w[i]，从物品0到物品i中选择物品放入背包中，。
c++用动态规划实现01背包问题
10-20
动态规划是解决这类问题的一种高效方法，它通过构建一个表格来存储子问题的解，避免了重复计算，从而提高了效率。 在C++中实现01背包问题，我们需要以下步骤： 1. **理解问题**：01背包问题描述为，给定一组物品，...
C++动态规划之背包问题解决方法
12-31
本文实例讲述了C++动态规划之背包问题解决方法。分享给大家供大家参考。具体分析如下： 问题描述： 背包的最大容量为W,有N件物品，每件物品重量为w,价值为p，怎样选择物品能使得背包里的物品价值最大？ 输入： 10 3...
Java学习之动态规划-背包问题代码
05-16
在编程领域，动态规划是一种强大的算法，常用于解决复杂的问题，比如背包问题。本文将深入探讨Java中的动态规划实现，特别是在解决背包问题时的应用。背包问题是一个经典的优化问题，它通常涉及在一个容量有限的背包...
Python基于动态规划算法解决01背包问题实例
12-25
本文实例讲述了Python基于动态规划算法解决01背包问题。分享给大家供大家参考，具体如下： 在01背包问题中，在选择是否要把一个物品加到背包中，必须把该物品加进去的子问题的解与不取该物品的子问题的解进行比较，...
动态规划——背包问题
Ten_years_star的博客
08-17 2598
对于背包问题，今天我们先讲解，01背包，完全背包，和多重背包。
动态规划之背包问题（全）
qq_63157868的博客
02-10 1561
（2）状态计算（如何求f[i][j]）：将f[i][j]看作集合，划分为不包含第i组的物品和包含第i组的第k个物品两类，不包含第i组的物品为从前i-1组物品选，总体积不超过j所构成的集合，取最大值，即f[i-1][j]，包含第i组的第k个物品为从前i-1个物品选，总体积不超过j-v[i,k]的集合，取最大值然后加上选取第i组物品的第k个物品的权重，即f[i-1][j-v[i,k]]+w[i,k]；
动态规划---背包问题
xhuyang111的博客
05-10 992
0-1背包问题 最常见的0-1背包问题，改问题描述如下: 有一个课装载重量为W的背包和N个商品，每个物品都有重量和价值两个属性，其中第i个商品的重量为wt[i],价值为val[i],现在用这个背包装商品，问最多能装的价值是多少？ 举个例子更直观吧: 高压锅重 4kg,价值300 风扇重 3kg,价值200 皮鞋重 1kg,价值150 背包总重4kg; 在面对一个动态规划时候，往往从以下几个方面分析，会有奇效: 本题中状态和选择是什么？ 这个例子中的状态很显然有两个，一个就是背包的重量W，一个
【算法】算法学习七：动态规划 | 背包问题 | 最长公共子串（含源代码）
wzk4869的博客
05-27 1706
【算法】算法学习七：动态规划 | 背包问题 | 最长公共子串（含源代码）
动态规划——背包问题（详解）
qq_61896131的博客
03-08 9099
动态规划是我最早接触的算法，一开始非常简单，固定模板题，后来愈发愈发难起来了，条件，状态压缩等等，难点主要是，状态怎么表示，状态转移方程怎么写，这篇文章将会从背包五大问题详解，希望能帮助到大家去类比，思考其他动态规划题目。 首先先来看看动态规划的定义： 动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。
动态规划-（0-1）背包问题
菜鸟的博客
10-29 1万+
下面我用容积代表重量（我是不会承认我看走眼了的。又懒得改。）0-1背包问题是动态规划背包问题系列的最基础的一个问题。相对理解起来较为简单。按书上来说，要证明一个问题是否可以使用动态规划思想，需要满足最优子结构的性质，那么什么是最优子结构的性质呢？书上给出的定义如下图看起来很拗口，其实就是不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。说白了就是一个最优策略的子策略也是必须是最优的，而所有子问题的局部最优解将导致整个问题的全局最优。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

CodePanda@GPF

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值