论文阅读”A deep variational approach to clustering survival data“(ICLR2022)

不吃香菜的zbw

已于 2022-08-03 10:56:44 修改

阅读量233

点赞数

分类专栏：论文阅读文章标签：深度学习人工智能聚类

于 2022-08-02 20:09:23 首次发布

本文链接：https://blog.csdn.net/qq_43497436/article/details/126121621

版权

论文阅读专栏收录该内容

39 篇文章 11 订阅

订阅专栏

论文标题

A deep variational approach to clustering survival data

论文作者、链接

作者：

Manduchi, Laura and Marcinkevi{\v{c}}s, Ri{\v{c}}ards and Massi, Michela C and Weikert, Thomas and Sauter, Alexander and Gotta, Verena and M{\"u}ller, Timothy and Vasella, Flavio and Neidert, Marian C and Pfister, Marc and others

链接：https://arxiv.org/abs/2106.05763

Introduction逻辑（论文动机&现有工作存在的问题）

生存分析（Survival analysis），在很多医疗场景下有广泛的应用，用来推断解释变量（explanatory variables )和潜在的检查结果（censored survival outcome）之间的关系——后者表示某一事件发生的时间，如死亡或癌症复发，并在只知道部分相关情况时可以审查出来——用机器学习来学习这些数据的非线性关系

聚类——不适用于生存结果（the survival outcomes）——无法保证聚类结果中的子簇是与患者的信息相关——本文专注于聚类survival data的半监督学习方法，该方法联合考虑解释变量和审查结果作为患者状态的指标

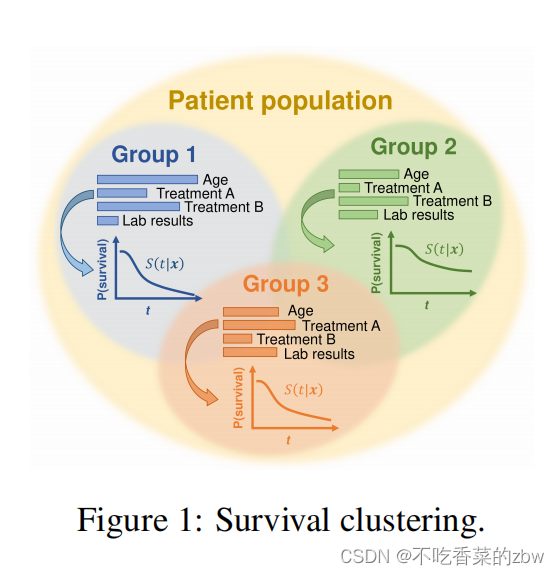
图1描述了这个聚类问题：整个患者群体由三个group组成，其特征是协变量和survival之间的不同关联，导致不同的临床情况

对于survival data的聚类——现有方法的局限：在高纬度的容量有限，无结构的数据以及专注于发现纯结果驱动的聚类——当仅凭survival distribution不足以对人群进行分层时，后者可能无法应用——相似survival outcome的患者可能需求不同的治疗手段

论文核心创新点

提出一个survival聚类方法，联合建模解释变量和censored survival outcomes

论文方法

预备知识

对于每一个患者有 $N$ 个三元组的数据集 $\mathcal{D}=\left\{\left(\boldsymbol{x}_{i}, \delta_{i}, t_{i}\right)\right\}_{i=1}^{N}$ 。 $x_i$ 代表特征的可解释变量。 $\delta _i$ 是检查指示变量，如果第 $i$ 个患者的survival time被审查了，值为0，否则值为1。 $t_i$ 是潜在的检查survival time。在survival analysis上用一个最大似然方法，来建模一个survival distribution，即 $S(t \mid \boldsymbol{x})=P(T>t \mid \boldsymbol{x})$ 。

对于survival analysis的两个主要的挑战，（i）survival times 的检查（ii） $x,t$ 之间的复杂非线性关系。当对survival data进行聚类的时候，我们额外的考虑了一个在训练过程中观测到的潜在聚类分配变量 $c_i \in \{1,\dots,K\}$ ， $K$ 是簇的总数目。于是目标问题变成了：（i）推测未观测到的聚类分布（ii）在给定 $x_i,c_i$ 的情况下对survival distribution进行建模

生成模型

假设数据是由下列步骤随机生成的。

1，从分类分布 $c \sim p(c ; \pi)=\pi_{c}$ 中采样簇分布 $c \in \{1,\dots,K\}$

2，从高斯分布生成一个连续的潜在嵌入 $\boldsymbol{z} \in \mathbb{R}^J$ ，这个嵌入的均值和方差依赖于采样的簇： $c:\boldsymbol{z} \sim p\left(\boldsymbol{z} \mid c ;\left\{\boldsymbol{\mu}_{1}, \ldots, \boldsymbol{\mu}_{K}\right\},\left\{\boldsymbol{\Sigma}_{1}, \ldots, \boldsymbol{\Sigma}_{K}\right\}\right)=\mathcal{N}\left(\boldsymbol{z} ; \boldsymbol{\mu}_{c}, \boldsymbol{\Sigma}_{c}\right)$

3，解释变量 $\boldsymbol{x}$ 是从在 $\boldsymbol{z}$ 上的条件分布生成的， $\boldsymbol{z}: \boldsymbol{x} \sim p(\boldsymbol{x} \mid \boldsymbol{z} ; \boldsymbol{\gamma})$ ，其中对于二值特征有 $p(\boldsymbol{x} \mid \boldsymbol{z} ; \boldsymbol{\gamma})=\operatorname{Bernoulli}\left(\boldsymbol{x} ; \boldsymbol{\mu}_{\boldsymbol{\gamma}}\right)$ ，对于实值特征有 $\mathcal{N}\left(\boldsymbol{x} ; \boldsymbol{\mu}_{\boldsymbol{\gamma}}, \operatorname{diag}\left(\boldsymbol{\sigma}_{\boldsymbol{\gamma}}^{2}\right)\right)$ 。

至此， $\boldsymbol{\mu_\gamma},\boldsymbol{\sigma^2_\gamma}$ 由 $f(\boldsymbol{z};\boldsymbol{\gamma})$ 生成，为一个解码器神经网络，参数为 $\gamma$ 。

4，survival time $t$ 依赖于聚类分布 $c$ ，潜在变量 $z$ 和检查指示变量 $\delta$ ，即 $t \sim p(t|z,c)$

Survival Model

$p(t|z,c)$ 参考于具体的簇的survival model。假设给定 $z,c$ ，依据韦伯分布的未审查的survival time由 $Weibull(softplus(z^\top,\beta_c),k)$ 给定，其中 $softplus(x)=log(1+exp(x))$ ， $k$ 是形状参数， $\beta_c$ 是具体的簇的survival参数。为了简洁省略偏置项 $\beta_{c,0}$ 。观察 $softplus(z^\top\beta_c)$ 项，对应的是韦伯分布的尺度参数。带有尺度参数 $\lambda$ 以及形状 $k$ 的韦伯分布，有一个概率稠密函数，在 $x\geq 0$ 的情况下，有 $f(x ; \lambda, k)=\frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1} \exp \left(-\left(\frac{x}{\lambda}\right)^{k}\right)$ 。于是，从下列分布对right-censoring区域做出调整：

其中， $\boldsymbol{\beta}=\left\{\boldsymbol{\beta}_{1}, \ldots, \boldsymbol{\beta}_{K}\right\} ; \lambda_{c}^{\boldsymbol{z}}=\text { softplus }\left(\boldsymbol{z}^{\top} \boldsymbol{\beta}_{c}\right) ;$ 并且 $S(t \mid \boldsymbol{z}, c)=\int_{t=t}^{\infty} f\left(t ; \lambda_{c}^{\boldsymbol{z}}, k\right)$ 是surviva函数。至此，使用 $p(t|z,c)$ 作为 $p(t|z,c;\beta,k)$ 的缩写。本文中只考虑right-censoring的情况

联合概率分布

$x,t$ 的联合概率分布写成 $p(\boldsymbol{x}, t)=\int_{\boldsymbol{z}} \sum_{c=1}^{K} p(\boldsymbol{x}, t, \boldsymbol{z}, c)=\int_{\boldsymbol{z}} \sum_{c=1}^{K} p(\boldsymbol{x} \mid t, \boldsymbol{z}, c) p(t, \boldsymbol{z}, c)$ 。值得注意的是 $x,t$ 是与给定的 $z$ 所独立的。我们重写联合概率分布，参考似然函数，有：

置信下界

根据之前数据生成的假设，目标是推理参数 $\pi,\mu,\Sigma,\beta$ 。由于方程2中的似然函数是难以处理的，我们将数据的对数边际概率的下界最大化：

我们给出了具有变化分布的观测值z和c的近似概率 $q(\boldsymbol{z}, c \mid \boldsymbol{x}, t)=q(\boldsymbol{z} \mid \boldsymbol{x}) q(c \mid \boldsymbol{z}, t)$ 。其中第一项是由神经网络参数化的编码器。第二项等于真实概率 $p(c|z,t)$ :

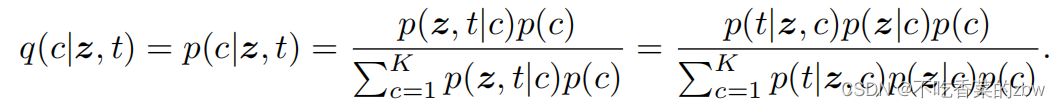
因此，证据下界(ELBO)可表示为:

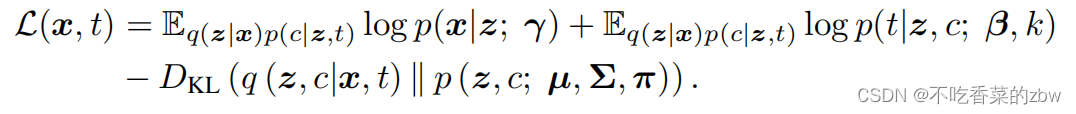
缺失的Survival Time

硬聚类分配可由式4的分布 $p(c|z, t)$ 计算。然而，在测试时可能无法观察到存活时间;
而我们对分布 $p(c|z, t)$ 的推导依赖于 $p(t|z, c)$ 。因此，当个体的生存时间未知时，我们使用贝叶斯规则计算，即：

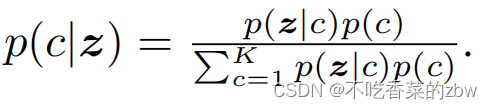
一句话总结

说实话没看懂

论文好句摘抄（个人向）

（1）Clustering, on the other hand, serves as a valuable tool in data-driven discovery and subtyping of diseases

不吃香菜的zbw

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
论文阅读”A deep variational approach to clustering survival data“(ICLR2022)

A deep variational approach to clustering survival data
复制链接

扫一扫