摘要
数据拟合是在假设模型结构已知的条件下最优确定模型中未知参数使预测值与数据吻合度最高,本文选取线性项加激活函数组成一个非线性模型,利用神经网络算法最优确定模型中的未知参数,利用随机搜索的方式确定函数模型,从而达到很好的拟合效果
关键词
BP神经网络 随机搜索 随机重启 参数优化 数据拟合 RELU
问题描述
数据拟合问题普遍存在,拟合问题本质上是在假设模型结构已知的条件下最优确定模型中未知参数以使得模型预测与数据的吻合度最高,即数据拟合问题往往描述为一个参数优化问题。
复杂工业过程对于模型精度的要求,线性模型往往不能满足。因此模型结构假设为非线性更为合理。此处我们假设模型结构为:

算法设计
BP神经网络是一种按照误差逆向传播训练的多层前馈神经网络。神经网络理论上可以拟合任意曲线,这一点已经得到了严格的数学证明。
- 三层神经网络模型

通常一个多层神经网络由L层构成,其中有1层输出层,1层输入层,L-2层隐藏层。输入层是神经网络的第一层,表示一列矩阵或多列矩阵的输入。输出层是神经网络的最后一层,表示网络的输出结果,通常是一列矩阵。隐藏层有L-2层,表示每一层神经元通过前向传播算法计算的结果矩阵。
在本程序中,采用3层神经网络。输入矩阵X=[X1,X2],题目中给出的模型需要对输入矩阵X进行增广,然后乘以参数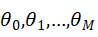 ,其实相当于神经网络中的偏置项bi,i=1,2。因此在本程序中无需对输入矩阵进行增广。wi,wi, i=1,2;bi,i=1,2分别是输入层与隐藏层之间,隐藏层与输出层之间的连接权重和偏置项。设
,其实相当于神经网络中的偏置项bi,i=1,2。因此在本程序中无需对输入矩阵进行增广。wi,wi, i=1,2;bi,i=1,2分别是输入层与隐藏层之间,隐藏层与输出层之间的连接权重和偏置项。设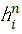 ,n=1,i=1,2,3,…,M,表示隐藏层的第i个神经元的输出。
,n=1,i=1,2,3,…,M,表示隐藏层的第i个神经元的输出。 - 激活函数
本程序中采用的激活函数为RELU函数,即函数模型中的,目的是去除整个神经网络输出的线性化,使得整个神经网络模型呈非线性化。 - 损失函数
本程序中采用的损失函数为MSE(均方误差),利用均方误差和激活函数的导数来更新权重和偏置。
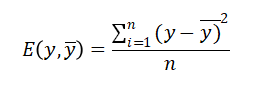
前向传播算法是指依次向前计算相邻隐藏层之间的连接输出,直到模型的最终输出值。其特点作用于相邻层的两个神经元之间的计算,且前一层神经元的输出是后一层的神经元的输入。
设对于第n层的第i个神经元,有n-1层的M(M为超参数)个神经元与该神经元有突触相连,则第n层第i个神经元的输入为: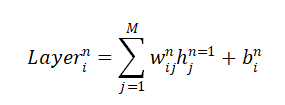
第n层的第i个神经元的输出为: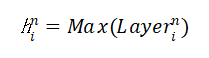
- 反向传播算法
结合前向传播的两个式子,得到第n层第i个神经元的输入与第n-1层第i个神经元的输出的关系为:
- 梯度下降算法
得到每一个隐藏层的连接权重和偏置项的梯度后,利用学习率和梯度下降算法更新每一层的连接权重和偏置项: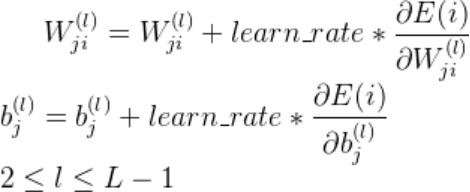
- 学习率更新策略
在配合梯度下降优化的过程中,如果学习率设置过大,则容易导致模型过拟合;如果设置过小,会使得模型优化的速度变得很缓慢。为此加入衰减因子和学习次数来计算模型每次学习的学习率:

- 归一化与反归一化


- 随机重启算法
为了防止更新参数时陷入局部极小,采用随机重启的方式更换初始参数状态。 - 超参数M的确定
本程序的超参数M的确定方法为随机搜索法,最终确定M的取值为20。 - 编程环境和程序主要函数说明
全部内容均在JetBrains发布的PyCharm社区版(版本号2019.2.5)编程环境中完成,使用的语言为Python,解释器为Python3.8。
#产生数据,并将产生的数据方阵降维,方便计算处理
def init(inpit_n_row):
#激活函数
def relu(x):
#激活函数RELU的导数
def d_relu(x):
#归一化数据
def normalize(data):
#反归一化数据
def d_normalize(norm_data, data):
#计算损失函数:平方损失函数
def quadratic_cost(y_, y):
#评价函数RSSE
def rsse(y_predict, y):
#前向传播算法
def prediction(l0, W, B):
#反向传播算法:根据损失函数优化各个隐藏层的权重
def optimizer(Layers, W, B, y, learn_rate):
#训练BP神经网络
def train(X, y, W, B, method, learn_rate):
#拟合曲面可视化
def visualize(y, inpit_n_row, input_n_col, hidden_n_1):
#为了解决陷入局部极小值,随机重启
def random_restart():
#main()函数
if name == ‘main’:
结果分析与讨论


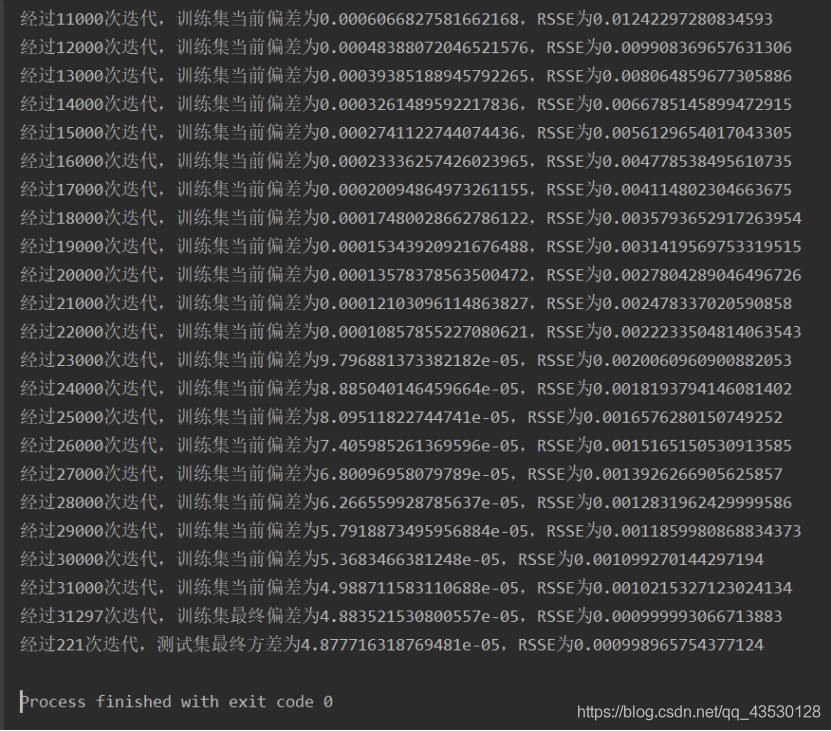
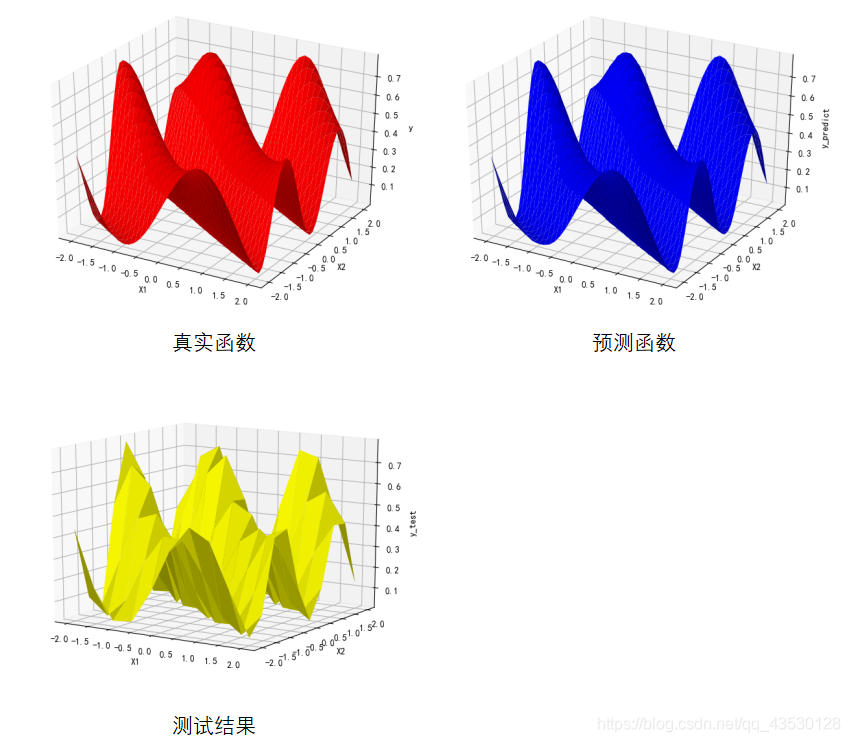
对于3232的训练集,需要几千次的迭代,即可使模型的RSSE值降到0.1以下,需要10000-32000次左右的迭代,即可使模型的RSSE值降到0.001以下;对于1010的测试集,需要30-90次的迭代即可使其RSSE值降到0.1以下,需要200-300次左右的迭代,即可使其的RSSE值降到0.001以下。
(2)抗噪测试
加入高斯白噪声:a = (np.random.random() - 0.5)/5
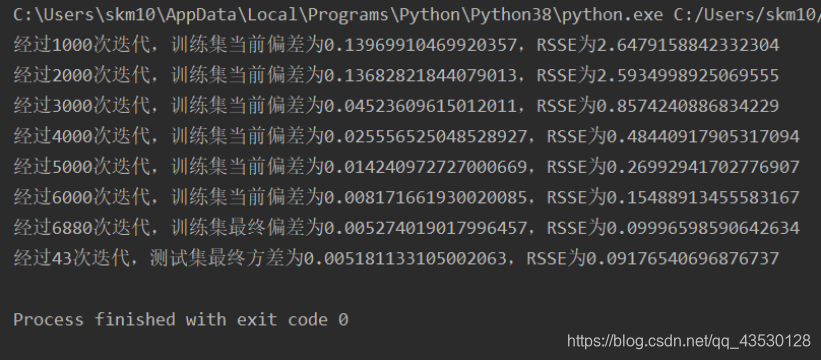
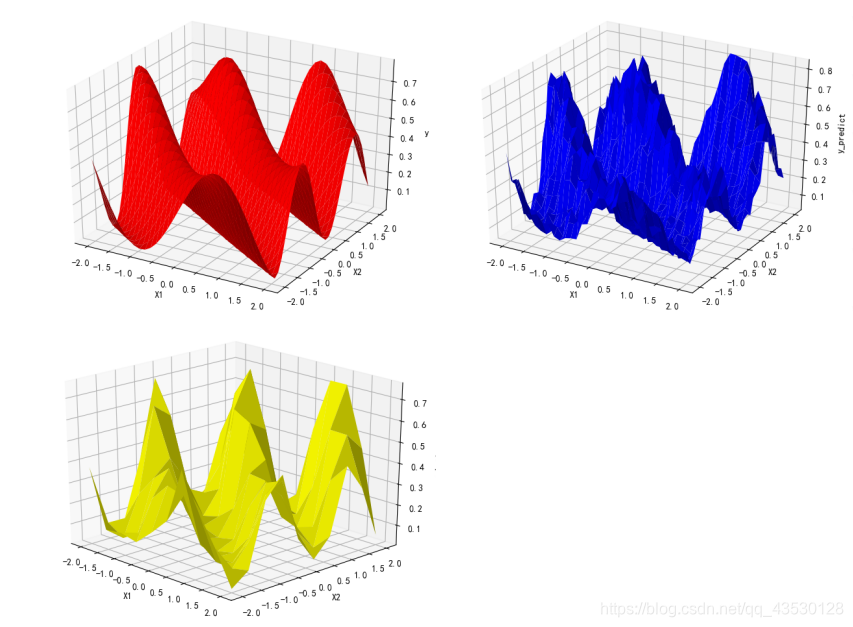
加入野值:
b = (np.random.randint(0, 9) - 0.5)/ 9
post = np.random.randint(0, inpit_n_row - 1)
y[post] += b
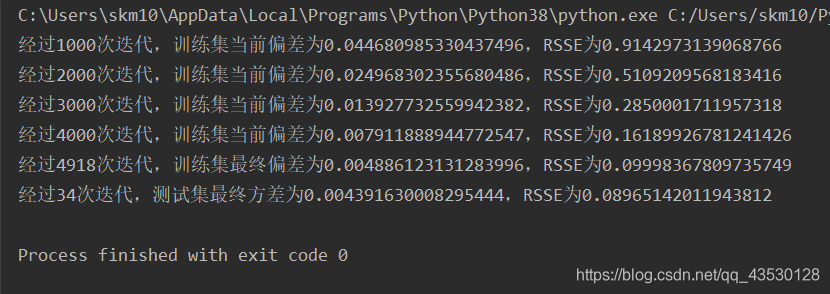
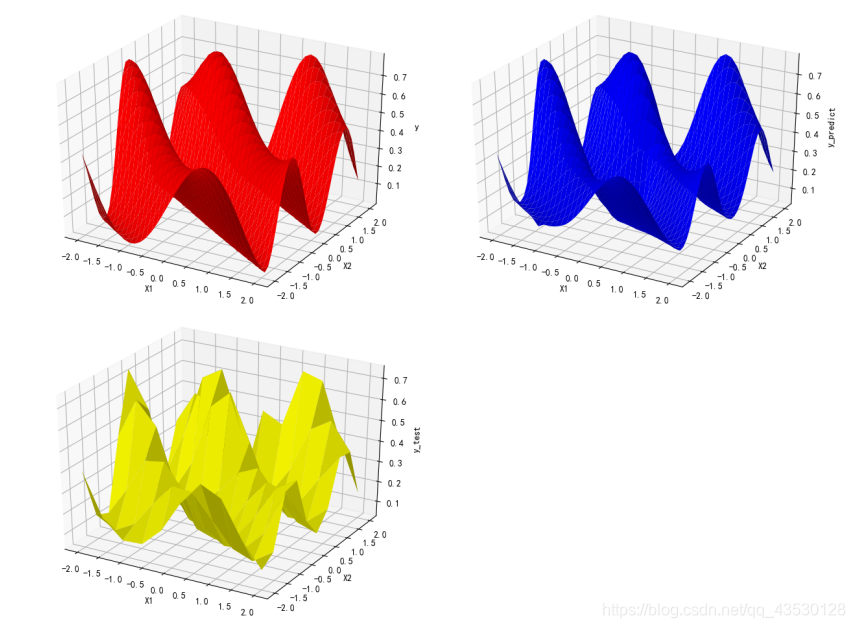
由此可见,模型的抗噪能力良好。
结论
- 神经网络具有实现任何复杂非线性映射的功能。
- BP神经网络的的学习速度慢,因其本质上是梯度下降法,必然会出现锯齿现象。
- 随机重启、模拟退火这些算法可以有效地解决陷入局部极值的问题。
Python源代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei']
#产生数据,并将产生的数据方阵降维,方便计算处理
def init(inpit_n_row):
X1 = np.linspace(-2, 2, int(inpit_n_row**0.5))
X2 = np.linspace(-2, 2, int(inpit_n_row**0.5))
X1, X2 = np.meshgrid(X1, X2)
X1 = X1.reshape(-1)
X2 = X2.reshape(-1)
x, y = [], []
for i in range(inpit_n_row):
# 增加高斯白噪声
#a = np.random.random() - 0.5
#a /= 5
x.append([X1[i], X2[i]])
Y = (1 + np.sin(2 * X1[i] + 3 * X2[i])) / (3.5 + np.sin(X1[i] - X2[i])) # + a
y.append(Y)
# 增加野值
'''b = np.random.randint(0, 9) - 0.5
b /= 9
post = np.random.randint(0, inpit_n_row - 1)
y[post] += b'''
x = np.array(x)
y = np.array([y]).T
return x,y
# 激活函数
def relu(x):
return np.maximum(0,x)
# 激活函数RELU的导数
def d_relu(x):
x[x<0] = 0
return x
# 归一化数据
def normalize(data):
data_min, data_max = data.min(), data.max()
data = (data - data_min) / (data_max - data_min)
return data
# 反归一化数据
def d_normalize(norm_data, data):
data_min, data_max = data.min(), data.max()
return norm_data * (data_max - data_min) + data_min
# 计算损失函数:平方损失函数
def quadratic_cost(y_, y):
inpit_n_row = len(y)
return np.sum(1 / inpit_n_row * np.square(y_ - y))
# 评价函数RSSE
def rsse(y_predict, y):
y_ = np.mean(y)
return np.sum(np.square(y_predict - y))/np.sum(np.square(y-y_))
# 前向传播算法
def prediction(l0, W, B):
Layers = [l0]
for i in range(len(W)):
Layers.append(relu(x=Layers[-1].dot(W[i]) + B[i]))
return Layers
# 反向传播算法:根据损失函数优化各个隐藏层的权重
def optimizer(Layers, W, B, y, learn_rate):
l_error_arr = [(y - Layers[-1]) * d_relu(x=Layers[-1])]
for i in range(len(W) - 1, 0, -1):
l_error_arr.append(l_error_arr[-1].dot(W[i].T) * d_relu(x=Layers[i]))
j = 0 # l_delta_arr = [err3, err2, err1]
for i in range(len(W) - 1, -1, -1):
W[i] += learn_rate * Layers[i].T.dot(l_error_arr[j]) # W3 += h2 * err3
B[i] += learn_rate * l_error_arr[j] # B3 += err3
j += 1
# 训练BP神经网络
def train(X, y, W, B, method, learn_rate):
#norm_X, norm_y = normalize(data=X), normalize(data=y) # 归一化处理
norm_X = X
norm_y = y # 由于测试模型无负值,无需归一化处理,可极大提高效率
#加了噪声之后,需降低精度要求,降低至0.1即可
end_loss = 0.001
step_arr, loss_arr, rsse_arr = [], [], []
step = 1
if method == '训练集':
error = '偏差'
else:
error = '方差'
while True:
Layers = prediction(l0=norm_X, W=W, B=B)
rsse_now = rsse(y_predict=Layers[-1], y=norm_y)
learn_rate_decay = learn_rate # * 1.0 / (1 + step * 0.001)
optimizer(Layers=Layers, W=W, B=B, y=y, learn_rate=learn_rate_decay)
cur_loss = quadratic_cost(y_=Layers[-1], y=norm_y)
if step % 1000 == 0:
step_arr.append(step)
loss_arr.append(cur_loss)
rsse_arr.append(rsse_now)
print('经过{}次迭代,{}当前{}为{},RSSE为{}'.format(step, method, error, cur_loss, rsse_now))
if rsse_now < end_loss:
# prediction_ys = d_normalize(norm_data=Layers[-1], data=y) # 反归一化结果
print('经过{}次迭代,{}最终{}为{},RSSE为{}'.format(step, method, error, cur_loss, rsse_now))
return 0, Layers[-1]
if len(rsse_arr) >= 2 and rsse_arr[-2] - rsse_arr[-1] < 1e-5 or step > 50000:
print('此初始权重可能导致算法陷入局部极值,故随机重启,重新迭代')
return -1, []
step += 1
# 拟合曲面可视化
def visualize(y, inpit_n_row, input_n_col, hidden_n_1):
z = []
for i in y:
for j in i:
z.append(j)
z = np.array(z).reshape(int(inpit_n_row**0.5), int(inpit_n_row**0.5))
# 代入训练好的模型测试
flag = -1
while flag == -1:
np.random.seed(random_restart())
# 产生测试集
test_n_row = 100
x_test, y_test = init(test_n_row)
W1 = np.random.randn(input_n_col, hidden_n_1) / np.sqrt(test_n_row)
b1 = np.zeros((test_n_row, hidden_n_1))
# 输出层权重矩阵
W2 = np.random.randn(hidden_n_1, 1) / np.sqrt(test_n_row)
b2 = np.zeros((test_n_row, 1))
w, b = [W1, W2], [b1, b2]
flag, y_test = train(x_test, y_test, w, b, '测试集', learn_rate=0.15)
z_test = []
for i in y_test:
for j in i:
z_test.append(j)
z_test = np.array(z_test).reshape(int(test_n_row ** 0.5), int(test_n_row ** 0.5))
# 拟合曲面可视化
X1 = np.linspace(-2, 2, int(inpit_n_row**0.5))
X2 = np.linspace(-2, 2, int(inpit_n_row**0.5))
X1, X2 = np.meshgrid(X1, X2)
Z = (1 + np.sin(2 * X1 + 3 * X2)) / (3.5 + np.sin(X1 - X2))
fig = plt.figure()
ax = Axes3D(fig)
# 画出真实函数
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('y')
ax.plot_surface(X1, X2, Z, color='red')
# 画出预测函数
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('y_predict')
ax.plot_surface(X1, X2, z, color='blue')
# 画出测试结果
X1 = np.linspace(-2, 2, int(test_n_row ** 0.5))
X2 = np.linspace(-2, 2, int(test_n_row ** 0.5))
X1, X2 = np.meshgrid(X1, X2)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('y_test')
ax.plot_surface(X1, X2, z_test, color='yellow')
plt.show()
# 为了解决陷入局部极小值,随机重启
def random_restart():
return np.random.randint(0, 23768)
if __name__ == '__main__':
# 样本点个数
inpit_n_row = 1024
# 输入维度
input_n_col = 2
# 神经元个数
hidden_n_1 = 20
flag = -1
while flag == -1:
np.random.seed(random_restart())
x, y = init(inpit_n_row)
# 第一个隐藏层权重矩阵
W1 = np.random.randn(input_n_col, hidden_n_1) / np.sqrt(inpit_n_row)
b1 = np.zeros((inpit_n_row, hidden_n_1))
# 输出层权重矩阵
W2 = np.random.randn(hidden_n_1, 1) / np.sqrt(inpit_n_row)
b2 = np.zeros((inpit_n_row, 1))
W, B = [W1, W2], [b1, b2]
flag, y = train(x, y, W, B, '训练集', learn_rate=0.001) # 开始训练BP神经网络
visualize(y, inpit_n_row, input_n_col, hidden_n_1)

























 3053
3053











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








